Sušení rajčat
 35 min.,
35 min.,  3/3
3/3 Sušení je považováno za jeden z nejstarších a zároveň z nejzdravějších způsobů dlouhodobého uchovávání potravin, který prodlouží jejich trvanlivost až na jeden rok. Je to způsob, jak uchovat chuť, vůni i barvu potravin. Výhodou je také, že usušené potraviny zabírají o hodně méně místa.
Jedná se o jednu z nejběžněji používaných konzervačních metod jak v domácnostech, tak ve zpracovatelském průmyslu. V domácnostech se ovoce, zelenina nebo houby suší volně na slunci, v troubě nebo v sušičce. Komerční sušení ovoce pak probíhá ve specializovaných sušárnách.
Při sušení je důležité, aby každý kus byl vystaven stálému proudění teplého vzduchu, čímž se odpařuje voda a klesá vlhkost. Vlhkost by měla klesnout na maximálně \(30\,\%\). Při této vlhkosti je zabráněno množení mikroorganizmů a plísní bez ohledu na obalový materiál a teplotu skladování.
Zadání
Jedním z typických druhů zeleniny, který se suší jsou rajčata. Ta někteří milovníci italské kuchyně považují za malý červený zázrak. Z hlediska sušení přitom rajčata patří mezi nejnáročnější, jelikož jsou tvořena z \(94\,\%\) vodou.
Všechna procenta v následujících úlohách jsou hmotnostní, tedy číselně představují počet gramů složky ve \(100\,\text{g}\) hmoty.
Úloha 1. Jestliže dojde v jednom kilogramu čerstvých rajčat po sušení k úbytku vody o jeden procentní bod, kolik gramů budou rajčata vážit? Pro zajímavost zkuste výsledek nejprve odhadnout.
Řešení. Jeden kilogram čerstvých rajčat je dle zadání tvořen \(940\,\text{g}\) vody a \(60\,\text{g}\) zbylých látek (tzv. sušiny). Po usušení na podíl vody \(93\,\%\) označme neznámou hmotnost rajčat \(x\) (v gramech). Protože sušina v rajčatech zůstává, váží v nich nyní voda \(x-60\,\text{g}\), tedy \[ \frac{x-60}{x} = \frac{93}{100}, \] jelikož podíl hmotnosti vody a celkové hmotnosti musí být právě \(93/100\). Řešením této rovnice je hmotnost rajčat \[x=\frac{6000}{7}\doteq 857{,}14\,\text{g}.\]
Úloha 2. Určete předpis a definiční obor funkce, která při sušení jednoho kilogramu čerstvých rajčat popisuje závislost aktuální hmotnosti rajčat na procentuálním podílu vody v nich obsažené. Načrtněte graf této funkce.
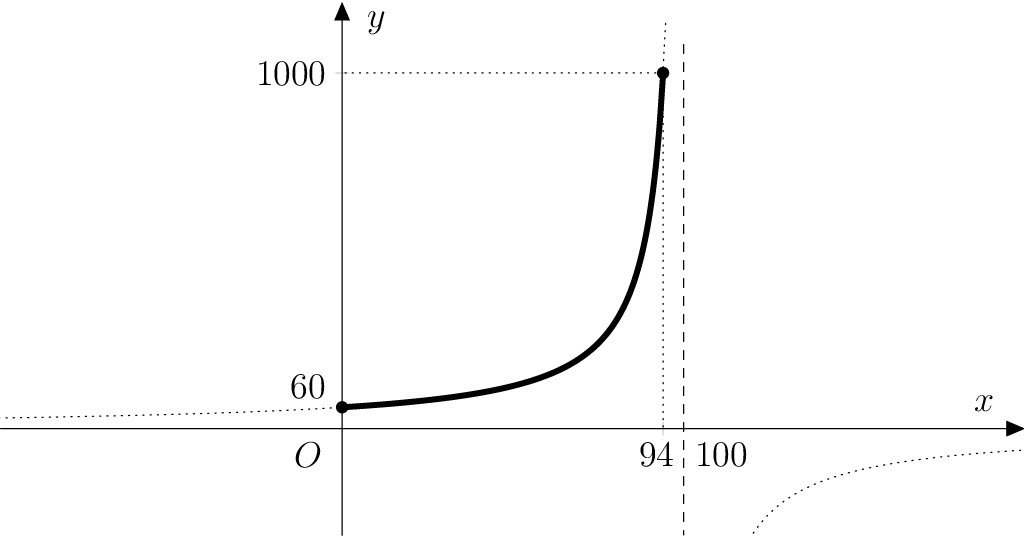
Řešení. Ze zadání víme, že nezávislá proměnná (označíme si ji jako obvykle \(x\)) je procentuálním podílem vody v rajčatech a závislá proměnná (označíme \(y\)) je aktuální hmotností rajčat (v gramech). Tedy platí \[ \frac{y-60}{y}=\frac{x}{100}. \tag{1} \] Odtud vyjádřením \(y\) dostáváme předpis hledané funkce \(f\): \[ f\colon y= -\frac{6000}{x-100}. \]
Definičním oborem této funkce je uzavřený interval \(\left\langle 0; 94 \right\rangle\), kde krajní hodnoty odpovídají rajčatům zcela zbaveným vody a čerstvým rajčatům s \(94\%\) obsahem vody. Graf funkce \(f\) leží na hyperbole, která je posunutým grafem funkce \(f_0\colon y = -\frac{6000}{x}\) o 100 jednotek ve směru kladné poloosy \(x\).
Úloha 3. Jak se předpis funkce z předchozí úlohy změní, budeme-li sušit obecně \(m\) gramů čerstvých rajčat?
Řešení. Vycházíme ze vztahu \((1)\) v řešení 2. úlohy, kde nahradíme číslo \(60\) (tj. hmotnost sušiny v gramech) obecným vyjádřením \(\frac{6}{100}m\), neboť sušina tvoří \(6\,\%\) hmotnosti čerstvých rajčat. Vyjádřením proměnné \(y\) pak dostáváme předpis funkce \(g\) (s parametrem \(m\)) jako
\[ g\colon y = -\frac{6m}{x-100}. \tag{2} \]
Úloha 4. Z kolika kilogramů čerstvých rajčat připravíme
- jeden kilogram sušených rajčat s \(10\%\) obsahem vody;
- \(500\,\text{g}\) sušených rajčat s \(20\%\) obsahem vody;
- \(250\,\text{g}\) sušených rajčat s \(40\%\) obsahem vody?
Řešení. Odkážeme-li se na funkci \(g\) z řešení 3. úlohy, ptáme se, pro které \(m\) prochází graf funkce \(g\) bodem o souřadnicích \([10;1000]\) (v případě a), resp. bodem se souřadnicemi \([20;500]\) (v případě b), resp. bodem \([40;250]\) (v případě c).
Postupným dosazením souřadnic tří zmíněných bodů za \(x\) a \(y\) v předpisu \((2)\) a vyřešením získaných lineárních rovnic dostáváme kořeny \(m_1=15\,000\), \(m_2=\frac{20\,000}{3}\) a \(m_3=2500\). Výsledky tedy jsou \(15\,\text{kg}\) (pro případ a), \(\frac{20}{3}\doteq 6{,}67\,\text{kg}\) (pro případ b) a \(2{,}5\,\text{kg}\) (pro případ c).
Literatura
- Richtrmocová, Barbora. Zdravotní a nutriční aspekty sušeného ovoce. Bakalářská práce. Masarykova univerzita, 2018.