Které kouzlo dokáže v přetíženém výtahu rozsvítit správnou kontrolku, stiskem tlačítka automatu připravit pomerančovou sodovku, po pár minutách zhasnout rozsvícená světla v chodbě domu nebo pohybovat s postavou na obrazovce počítače? O tyto a celou řadu dalších činností v reálném životě se starají logické obvody, které podrobněji prozkoumáme v následující sérii úloh.
Logické obvody se skládají z tzv. logických členů, které realizují logické operace. V úlohách budeme pracovat pouze se třemi základními logickými členy NOT (negace), AND (konjunkce) a OR (disjunkce). Na obrázku jsou vidět jejich příslušné symboly (dle americké normy ANSI/MIL) v logických obvodech. Jsou orientovány tak, aby směr vstupu byl zleva. Vstupy chápeme jako výroky, výstupy jsou pak výroky složené.
Pravdivostní hodnoty jsou v logických obvodech realizovány napětím, nízké napětí značí pravdivostní hondotu 0, vysoká úroveň napětí značí hodnotu 1. Pokud je např. u členu AND na vstupu A nízká úroveň napětí a na vstupu B vysoká úroveň, je na výstupu nízká úroveň napětí. Konkrétní hodnoty úrovní se liší dle konkrétního využití obvodu. Běžná je třeba nízká úroveň přibližně 0V, vysoká přibližně 5V.
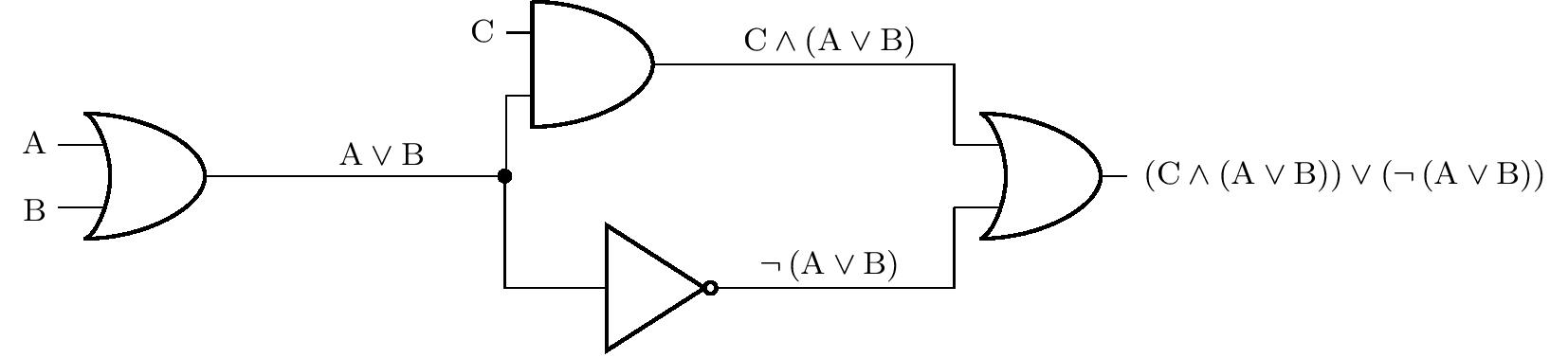
Na dalším obrázku vidíme znázornění jednoho složitějšího logického obvodu. Pro názornost je v obrázku také vyznačeno postupné skládání výroků, což odpovídá vstupům nebo výstupům jednotlivých členů. Černý puntík označuje uzel, ve kterém se logický obvod větví. Výstup jednoho členu tak může být přiveden na více vstupů zároveň.
V následujících úlohách mohou být před vstupy zařazeny spínače nebo tlačítka, za výstupy logického obvodu pak mohou být zařazeny žárovky. Dohodněme se, že na vstupu je logická hodnota rovna 1 právě tehdy, když je spínač sepnut nebo tlačítko stisknuto. Podobně žárovka svítí právě tehdy, když je na příslušném výstupu logická hodnota 1.
Úloha 1. V obvodu na předchozím obrázku jsou před vstupy A, B a C spínače a na výstupu je zapojena žárovka. Jestliže spínač C není sepnut, v jaké poloze musí být spínače A a B, aby žárovka svítila?
Řešení. Označme \(p(\mathrm{X})\) pravdivostní hodnotu výroku \(\mathrm{X}\). Ze zadání víme, že \(p(\mathrm{C})=0\), a ptáme se na hodnoty \(p(\mathrm{A})\) a \(p(\mathrm{B})\) takové, že \(p\left[ \left(\mathrm{C}\wedge \left(\mathrm{A}\vee\mathrm{B}\right)\right)\vee \left( \neg\left(\mathrm{A}\vee\mathrm{B}\right)\right) \right]=1\). Úlohu vyřešíme úvahou.
Jestliže platí \(p(\mathrm{C})=0\), pak nutně i \(p(\mathrm{C}\wedge \left(\mathrm{A}\vee\mathrm{B}\right))=0\). Proto musí být pravdivý výrok \(\neg ( \mathrm{A}\vee \mathrm{B})\), a tedy \(p(\mathrm{A}\vee \mathrm{B})=0\). To je však možné tehdy a jen tehdy, když jsou výroky \(\mathrm{A}\) i \(\mathrm{B}\) nepravdivé. Ani jeden spínač tak nesmí být sepnut.
Úloha 2. Je dán logický obvod na obrázku níže, na jehož vstupech A, B a C jsou spínače a na jehož výstupu Z je zapojena žárovka. Které spínače musíme sepnout, aby se žárovka rozsvítila? Nalezněte všechna řešení úlohy. Kříží-li se v diagramu vodiče bez znázorněného uzlu, předpokládá se, že ve skutečnosti ke styku vodičů nedochází.
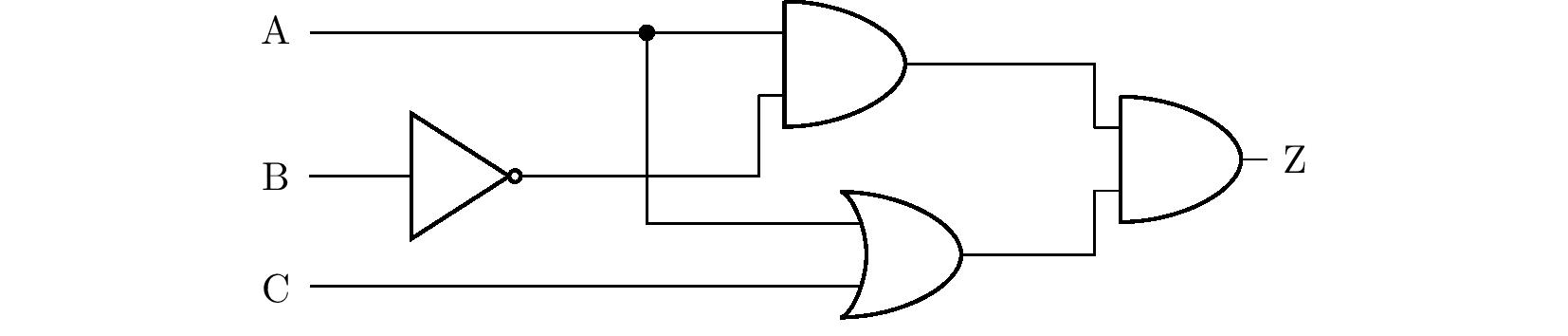
Řešení. Úlohu budeme řešit užitím tabulky pravdivostních hodnot. Z diagramu v zadání nejprve odvodíme výrok složený z výroků \(\mathrm{A}\), \(\mathrm{B}\) a \(\mathrm{C}\), který bude ekvivalentní výroku \(\mathrm{Z}\), viz obrázek.
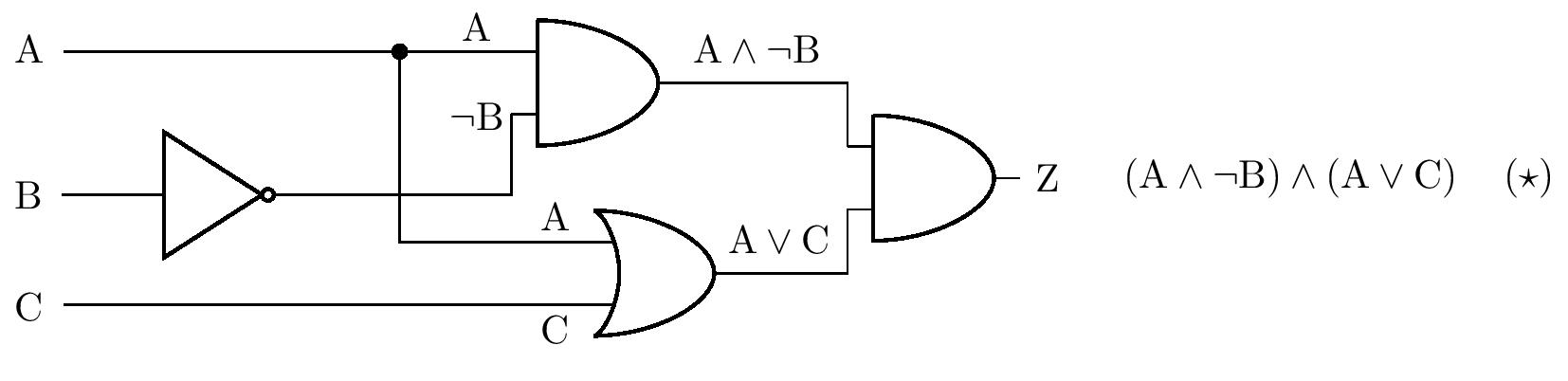
Pro složený výrok \(\left( \star \right)\) nyní vytvoříme tabulku pravdivostních hodnot:
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{C}\) | \(\mathrm{A}\wedge\neg\mathrm{B}\) | \(\mathrm{A}\vee\mathrm{C}\) | \(\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \wedge \left( \mathrm{A}\vee\mathrm{C} \right)\) |
|---|---|---|---|---|---|
| \(1\) | \(1\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(1\) | \(1\) | \(0\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(1\) | \(0\) | \(1\) | \(\quad1\) | \(\quad1\) | \(\qquad\qquad1\) |
| \(1\) | \(0\) | \(0\) | \(\quad1\) | \(\quad1\) | \(\qquad\qquad1\) |
| \(0\) | \(1\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(0\) | \(1\) | \(0\) | \(\quad0\) | \(\quad0\) | \(\qquad\qquad0\) |
| \(0\) | \(0\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(0\) | \(0\) | \(0\) | \(\quad0\) | \(\quad0\) | \(\qquad\qquad0\) |
Z tabulky vyplývá, že žárovka bude svítit, jestliže bude sepnutý spínač A a zároveň nebude sepnutý spínač B. Na sepnutí spínače C přitom nezáleží.
Úlohu lze řešit také ekvivalentními úpravami výroku \(\left(\star \right)\). Nejprve použijeme distributivní zákon, následně tzv. zákon idempotence \(\mathrm{A}\wedge \mathrm{A}\Leftrightarrow \mathrm{A}\):
\[ \begin{alignat*}{3} &&&\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \wedge \left( \mathrm{A}\vee\mathrm{C} \right) &&\quad\Leftrightarrow\\ &\Leftrightarrow\quad &&\left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{A}\right) \vee \left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{C}\right) &&\quad\Leftrightarrow\\ &\Leftrightarrow\quad &&\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \vee \left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{C}\right). && \tag{$\star\star$} \end{alignat*} \]
Složený výrok \(\left( \star\star \right)\) je však pravdivý právě tehdy, když je pravdivá konjunkce \(\mathrm{A}\wedge\neg\mathrm{B}\), tedy když je \(\mathrm{A}\) pravdivý výrok a \(\mathrm{B}\) nepravdivý výrok. Z toho vyplývá o poloze spínačů stejný závěr, který jsme učinili pomocí tabulky.
Úloha 3. Navrhněte logický obvod, který v případě poruchy některého ze dvou vodních čerpadel (příp. obou) rozsvítí výstražnou žárovku na výstupu obvodu. Dokud přitom čerpadlo funguje, vysílá signál odpovídající logické jedničce na jeden ze dvou vstupů obvodu.
Řešení. Označme \(\mathrm{A}\) a \(\mathrm{B}\) výroky představující stav prvního a druhého čerpadla. Hledáme výrok \(\mathrm{Z}\) složený z \(\mathrm{A}\) a \(\mathrm{B}\), jehož tabulku pravdivostních hodnot známe:
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{Z}\) |
|---|---|---|
| \(1\) | \(1\) | \(0\) |
| \(1\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(1\) |
Z tabulky jde poznat, že ekvivalentním výrokem je např. \(\neg\left( \mathrm{A} \wedge \mathrm{B}\right)\), kterému odpovídá diagram výsledného obvodu na obrázku:
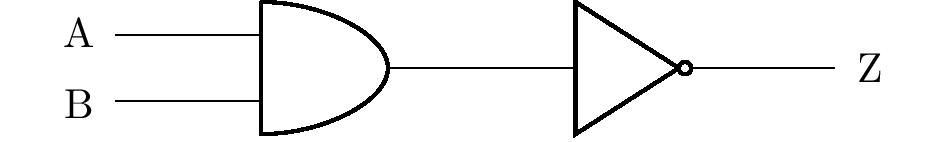
Úloha má více řešení. Například užitím de Morganova zákona dostáváme z předchozího výsledku ekvivalentní výrok \(\neg\mathrm{A}\vee\neg\mathrm{B}\). Tomuto výroku by odpovídal jiný, ale také správný, obvod (diagram).
Úloha 4. Modifikujte výstražné zařízení z předchozí úlohy. Na dvou výstupech nyní bude zapojeno červené a zelené světlo. Fungují-li obě čerpadla, svítí zelené světlo a červené je zhasnuté. Při poruše jednoho z čerpadel se navíc rozsvítí i červené světlo a při poruše obou čerpadel bude svítit pouze červené světlo. Navrhněte odpovídající logický obvod.
Řešení. Podobně jako v předchozí úloze označme \(\mathrm{A}\) a \(\mathrm{B}\) výroky představující stav prvního a druhého čerpadla. Dostaneme tak tabulku pravdivostních hodnot neznámých složených výroků \(\mathrm{Č}\) (červené světlo) a \(\mathrm{Z}\) (zelené světlo):
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{Č}\) | \(\mathrm{Z}\) |
|---|---|---|---|
| \(1\) | \(1\) | \(0\) | \(1\) |
| \(1\) | \(0\) | \(1\) | \(1\) |
| \(0\) | \(1\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(1\) | \(0\) |
Je vidět, že sloupec pro výrok \(\mathrm{Č}\) je totožný s výrokem \(\mathrm{Z}\) v předchozí úloze (a tedy můžeme převzít její řešení), a sloupec pro výrok \(\mathrm{Z}\) odpovídá disjunkci \(\mathrm{A}\vee \mathrm{B}\). Využitím uzlů a rozvětvením obvodu tak můžeme zakreslit diagram odpovídajícího logického obvodu:
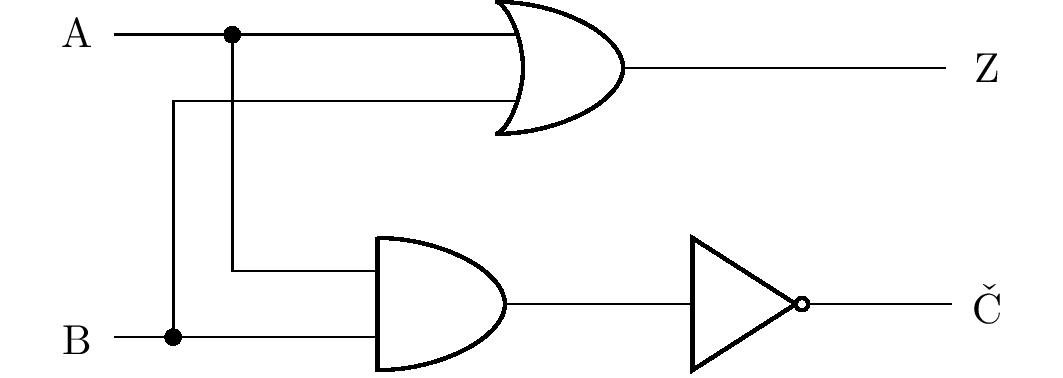
Podobně jako předchozí úloha má i tato více řešení, jejichž správnost je možné ověřit vždy pomocí tabulky pravdivostních hodnot. Blíže se však vyjádříme ještě k jednomu řešení.
Žáky může napadnout, že místo členu OR je možné vodiče spojit prostým uzlem, jak je znázorněno na obrázku:
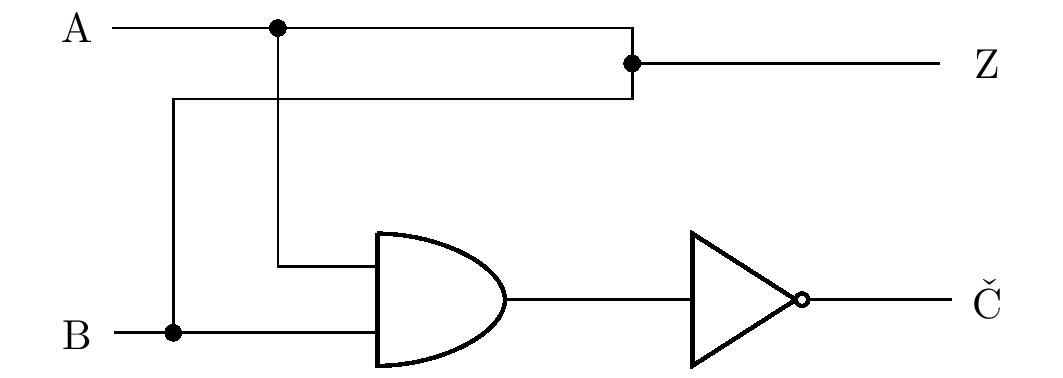
Jestliže bude na \(\mathrm{A}\) nebo \(\mathrm{B}\) (popř. na obou) hodnota \(1\), může tato hodnota volně protéct i na výstup \(\mathrm{Z}\,\)? Skutečnost je taková, že nikoliv. V úvodním odstavci jsme si řekli, že pravdivostní hodnota \(1\) se realizuje vysokou úrovní napětí a hodnota \(0\) jeho nízkou úrovní. Bude-li tak např. na vstupu \(\mathrm{A}\) vysoké a na vstupu \(\mathrm{B}\) nízké napětí, dojde v obvodu ke zkratu, neboť jsou vodičem spojeny body s různým napětím. Proto obecně nemůžeme v logických obvodech spojit výstupy různých členů uzly.
Úloha 5. Navrhněte logický obvod se dvěma vstupy a jedním výstupem, který simuluje operaci logické ekvivalence.
Řešení. Abychom mohli obvod sestrojit, potřebujeme nalézt k ekvivalenci \(\mathrm{A}\Leftrightarrow\mathrm{B}\) složený výrok se stejnou tabulkou pravdivostních hodnot, který obsahuje pouze konjunkce, disjunkce nebo negace. Z definice pro ekvivalenci plyne, že je pravdivá právě tehdy, jsou-li výroky \(\mathrm{A}\) a \(\mathrm{B}\) oba pravdivé nebo oba nepravdivé. To znamená, že je pravdivá právě tehdy, když je pravdivá konjunkce \(\mathrm{A}\wedge\mathrm{B}\) nebo je pravdivá konjunkce \(\neg\mathrm{A}\wedge\neg\mathrm{B}\). Tak dostáváme ekvivalenci \[ \left( \mathrm{A}\Leftrightarrow\mathrm{B} \right) \quad \Leftrightarrow \quad \left( \mathrm{A}\wedge\mathrm{B} \right) \vee \left( \neg\mathrm{A}\wedge\neg\mathrm{B} \right), \] jejíž pravá strana je výrok obsahující pouze konjunkce, disjunkci a negace. Můžeme proto sestavit odpovídající diagram:
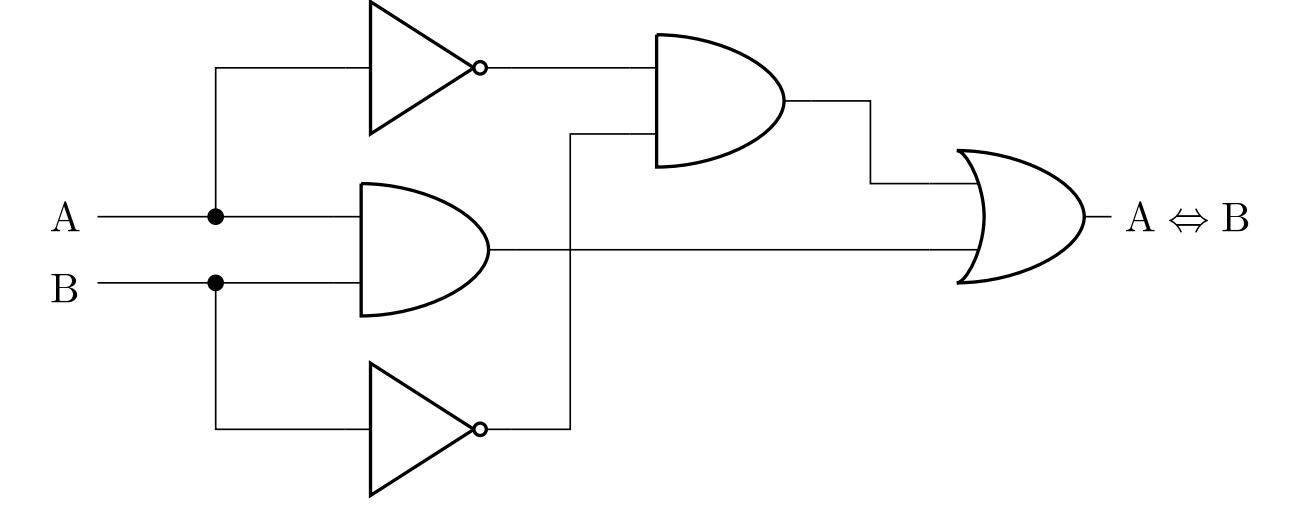
Jedno z dalších možných řešení můžeme dostat využitím de Morganových zákonů a ekvivalentní úpravou předchozího výsledku na výrok \(\left( \mathrm{A}\wedge\mathrm{B} \right) \vee \neg \left( \mathrm{A}\vee\mathrm{B} \right)\). Technickou výhodou tohoto tvaru je menší počet potřebných logických členů při realizaci obvodu.
Úloha 6. Kávový automat po stisku příslušného tlačítka umí připravit tři typy nápojů: lungo, macchiato a kakao. Nápoje se připravují mícháním čtyř ingrediencí (horké vody, mléka, kávového a kakaového koncentrátu), kde každá ingredience má svoji trysku. Navrhněte logický obvod se třemi vstupy (pro každý nápoj jeden) a čtyřmi výstupy (pro ventil každé trysky jeden), jestliže se lungo připravuje z vody a kávového koncentrátu, macchiato z vody, mléka a kávového koncentrátu a kakao z vody a kakaového koncentrátu.
Pro jednoduchost předpokládejme, že nikoho nenapadne zmáčknout více tlačítek najednou, tedy se těmito případy nemusíte zabývat. Ingredience je do kelímku uvolněna právě tehdy, když je na příslušném výstupu logická jednička.
Řešení. Označme \(\mathrm{C}\) (kakao, angl. cocoa), \(\mathrm{L}\) (lungo) a \(\mathrm{M}\) (macchiato) výroky představující stav stisknutí příslušného tlačítka a dále označme \(\mathrm{COC}\) (kakaový koncentrát, angl. cocoa concentrate), \(\mathrm{WA}\) (voda, angl. water), \(\mathrm{COF}\) (kávový koncentrát, angl. coffee concentrate) a \(\mathrm{ML}\) (mléko, angl. milk) výroky představující stav otevření příslušné trysky. Z informací v zadání pak sestavme tabulku pravdivostních hodnot:
| \(\mathrm{C}\) | \(\mathrm{L}\) | \(\mathrm{M}\) | \(\mathrm{COC}\) | \(\mathrm{WA}\) | \(\mathrm{COF}\) | \(\mathrm{ML}\) |
|---|---|---|---|---|---|---|
| \(1\) | \(0\) | \(0\) | \(1\) | \(1\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(0\) | \(0\) | \(1\) | \(1\) | \(0\) |
| \(0\) | \(0\) | \(1\) | \(0\) | \(1\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) |
Řádky, pro něž je v prvních třech sloupcích více než jedna jednička, nebereme v potaz, protože je možné zmáčknout vždy jen jedno tlačítko.
Z tabulky plyne, že ekvivalentní dvojicí výroků je \(\mathrm{COC}\) a \(\mathrm{C}\) a další ekvivalentní dvojicí jsou výroky \(\mathrm{ML}\) a \(\mathrm{M}\). Výrok \(\mathrm{COF}\) je pravdivý právě tehdy, když je pravdivý některý z výroků \(\mathrm{L}\) nebo \(\mathrm{M}\), tedy je ekvivalentní s disjunkcí \(\mathrm{L}\vee\mathrm{M}\). A konečně výrok \(\mathrm{WA}\) je pravdivý právě tehdy, když je některý z trojice výroků \(\mathrm{C}\), \(\mathrm{L}\), \(\mathrm{M}\) pravdivý, tedy je \(\mathrm{WA}\) ekvivalentní s disjunkcí \(\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}\).
Na následujícím obrázku je znázorněn diagram příslušného obvodu - disjunkce \(\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}\) je v něm přitom realizována vnořením dvou členů OR, tj. jako \(\mathrm{C}\vee\left( \mathrm{L}\vee\mathrm{M}\right)\).
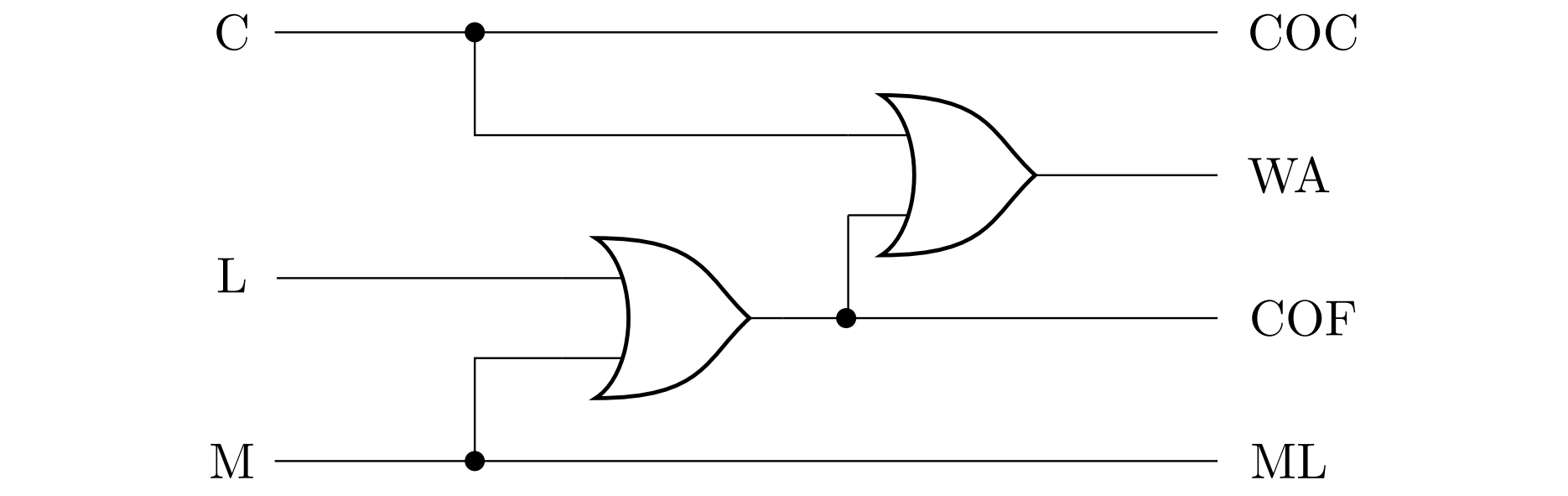
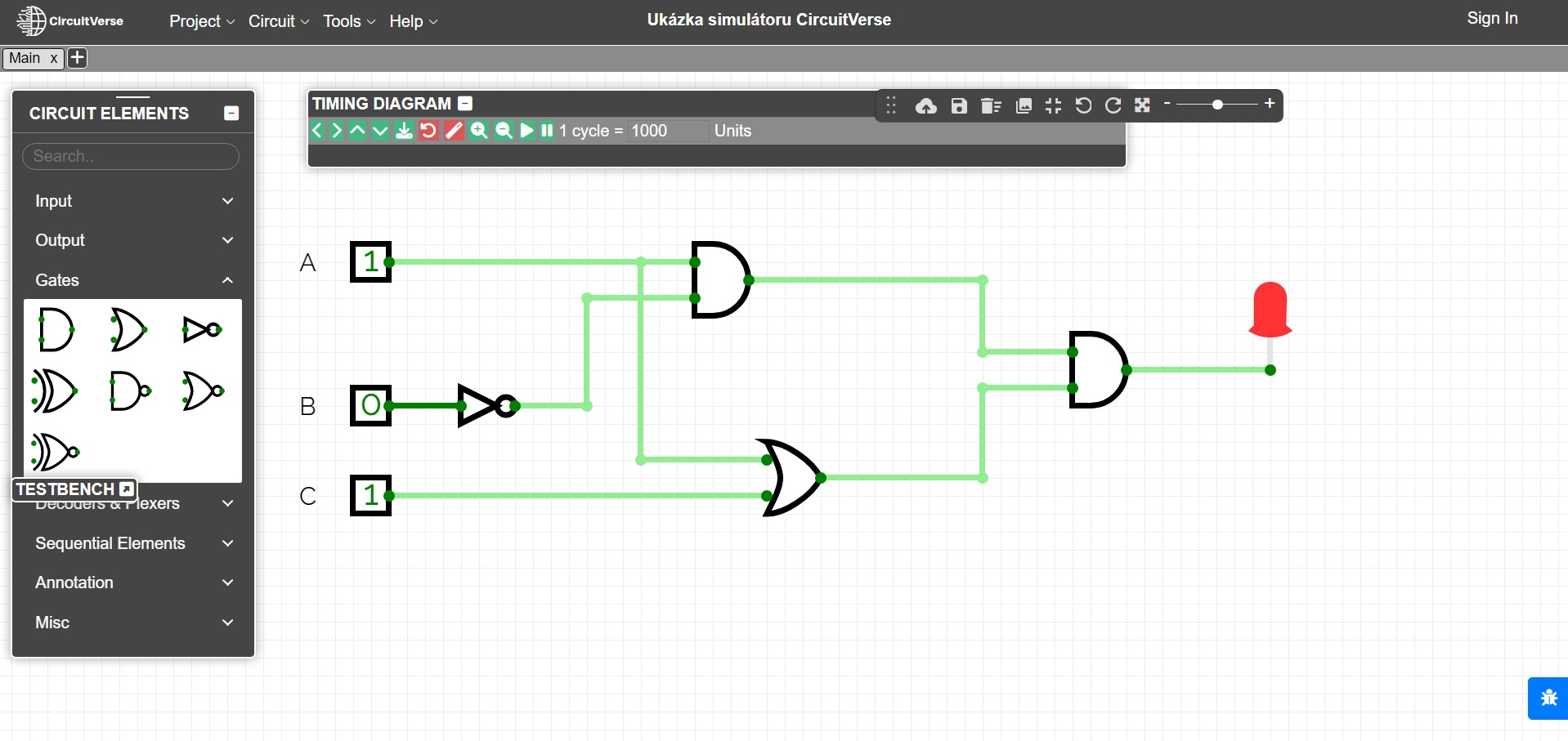
Všechny uvedené úlohy je možné názorně ilustrovat na různých simulátorech logických obvodů, např. online simulátoru CircuitVerse. Na posledním obrázku je v tomto simulátoru modelován obvod z Úlohy 2. K ilustraci je také možné využít specializovaných elektronických stavebnic.
