Sušenie paradajok
 35 min.,
35 min.,  3/3
3/3 Sušenie je považované za jeden z najstarších a zároveň najzdravších spôsobov dlhodobého uchovávania potravín, ktorý predĺži ich trvanlivosť až na jeden rok. Je to spôsob, ako zachovať chuť, vôňu aj farbu potravín. Výhodou je aj to, že usušené potraviny zaberajú oveľa menej miesta. Ide o jednu z najbežnejšie používaných konzervačných metód tak v domácnostiach, ako aj v spracovateľskom priemysle. V domácnostiach sa ovocie, zelenina či huby sušia voľne na slnku, v rúre alebo v sušičke. Komerčné sušenie ovocia prebieha v špecializovaných sušiarňach. Pri sušení je dôležité, aby každý kus bol vystavený stálemu prúdeniu teplého vzduchu, čím sa odparuje voda a znižuje sa vlhkosť. Vlhkosť by mala klesnúť na maximálne \(30\,\%\). Pri tejto vlhkosti je zabránené množeniu mikroorganizmov a plesní bez ohľadu na obalový materiál a teplotu skladovania.
Zadanie
Jedným z typických druhov zeleniny, ktorý sa suší, sú paradajky. Niektorí milovníci talianskej kuchyne ich považujú za malý červený zázrak. Z hľadiska sušenia však paradajky patria medzi najnáročnejšie, keďže sú tvorené z \(94\,\%\) vodou. Všetky percentá v nasledujúcich úlohách sú hmotnostné, teda číselne predstavujú počet gramov zložky v \(100\,\text{g}\) hmoty.
Úloha 1. Ak dôjde v jednom kilograme čerstvých paradajok po sušení k úbytku vody o jeden percentuálny bod, koľko gramov budú paradajky vážiť? Pre zaujímavosť skúste výsledok najprv odhadnúť.
Riešenie. Jeden kilogram čerstvých paradajok je podľa zadania tvorený \(940\,\text{g}\) vody a \(60\,\text{g}\) sušiny. Po sušení predpokladajme, že celková hmotnosť paradajok je \(x\) (v gramoch) a že podiel vody tvorí \(93\,\%\). Keďže sušina zostáva nezmenená, hmotnosť vody je \(x-60\,\text{g}\). Platí teda vzťah \[ \frac{x-60}{x} = \frac{93}{100}, \] ktorý udáva podiel vody na celkovej hmotnosti. Riešením tejto rovnice je \[x=\frac{6000}{7}\doteq 857{,}14\,\text{g}.\]
Úloha 2. Určte predpis a definičný obor funkcie, ktorá pri sušení jedného kilogramu čerstvých paradajok popisuje závislosť aktuálnej hmotnosti paradajok na percentuálnom obsahu vody v nich. Načrtnite graf tejto funkcie.
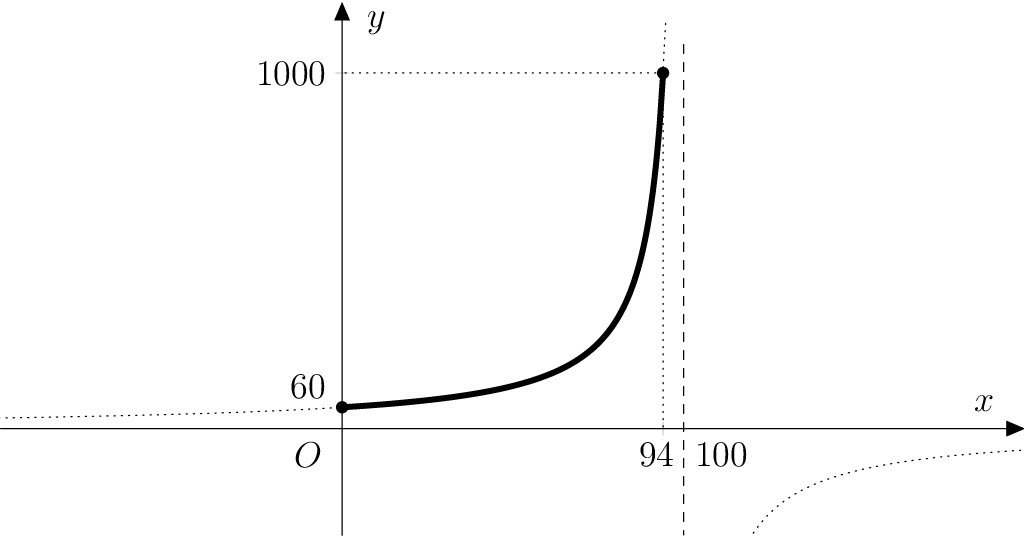
Riešenie. Zo zadanie vieme, že nezávislá premenná \(x\) je percentuálny podiel vody v paradajkách a závislá premenná \(y\) je aktuálna hmotnosť paradajok (v gramoch). Platí \[ \frac{y-60}{y}=\frac{x}{100}. \tag{1} \] Vyjadrením \(y\) získame predpis funkcie \(f\): \[ f\colon y= -\frac{6000}{x-100}. \]
Definičný obor funkcie je uzavretý interval \(\left\langle 0; 94 \right\rangle\), kde hraničné hodnoty zodpovedajú paradajkám úplne zbaveným vody a čerstvým paradajkám s obsahom vody \(94\,\%\). Graf funkcie \(f\) leží na hyperbole, ktorá je posunutým grafom funkcie \(f_0\colon y = -\frac{6000}{x}\) o 100 jednotiek v kladnom smere osi \(x\).
Úloha 3. Ako sa zmení predpis funkcie z predchádzajúcej úlohy, ak budeme sušiť všeobecne \(m\) gramov čerstvých paradajok?
Riešenie. Vyjdeme zo vzťahu \((1)\) z riešenia 2. úlohy, kde číslo \(60\) (hmotnosť sušiny v gramoch) nahradíme výrazom \(\frac{6}{100}m\), pretože sušina tvorí \(6\,\%\) hmotnosti čerstvých paradajok. Vyjadrením premennej \(y\) získame predpis funkcie \(g\) (s parametrom \(m\)) ako \[ g\colon y = -\frac{6m}{x-100}. \tag{2} \]
Úloha 4. Z koľkých kilogramov čerstvých paradajok pripravíme a. jeden kilogram sušených paradajok s \(10\%\) obsahom vody; b. \(500\,\text{g}\) sušených paradajok s \(20\%\) obsahom vody; c. \(250\,\text{g}\) sušených paradajok s \(40\%\) obsahom vody?
Riešenie. Odkážeme sa na funkciu \(g\) z riešenia 3. úlohy, kde hľadáme hodnoty \(m\), pre ktoré graf funkcie \(g\) obsahuje body so súradnicami \([10;1000]\) (v prípade a), bodom so súradnicami \([20;500]\) (v prípade b), bodom \([40;250]\) (v prípade c).
Dosadením týchto súradníc za \(x\) a \(y\) do predpisu \((2)\) a vyriešením vzniknutých lineárnych rovníc dostávame korene \(m_1=15\,000\), \(m_2=\frac{20\,000}{3}\) a \(m_3=2500\). Výsledky sú teda \(15\,\text{kg}\) (pre prípad a), \(\frac{20}{3}\doteq 6{,}67\,\text{kg}\) (pre prípad b) a \(2{,}5\,\text{kg}\) (pre prípad c).
Literatúra
- Richtrmocová, Barbora. Zdravotní a nutriční aspekty sušeného ovoce. Bakalářská práce. Masarykova univerzita, 2018.