Suszenie jest jedną z najstarszych i najzdrowszych metod długoterminowego przechowywania żywności, Wydłuża okres przydatności żywności do spożycia nawet o rok. Jest to sposób na zachowanie smaku, zapachu i koloru żywności. Kolejną zaletą jest to, że suszona żywność zajmuje znacznie mniej miejsca.
Jest to jedna z najczęściej stosowanych metod konserwacji zarówno w gospodarstwach domowych, jak i w przemyśle przetwórczym. W gospodarstwach domowych owoce, warzywa lub grzyby suszy się swobodnie na słońcu, w piekarniku lub w suszarce. Komercyjne suszenie owoców odbywa się następnie w specjalistycznych suszarkach.
Podczas suszenia ważne jest, aby każdy kawałek był wystawiony na stały przepływ ciepłego powietrza, które odparowuje wodę i obniża wilgotność. Wilgotność powinna spaść do maksymalnie 30%. Przy takiej wilgotności zapobiega się rozwojowi mikroorganizmów i pleśni, niezależnie od materiału opakowania i temperatury przechowywania.
Pomidory są jednym z typowych suszonych warzyw. Niektórzy miłośnicy kuchni włoskiej uważają je za mały czerwony cud. Pod względem suszenia, pomidory są jednymi z najbardziej wymagających, ponieważ składają się z 94% wody.
Wszystkie wartości procentowe w poniższych ćwiczeniach wyrażają ułamki masowe, tj. liczbowo reprezentują liczbę gramów składnika w \(100\text{g}\) masy.
Ćwiczenie 1. Jeśli kilogram świeżych pomidorów straci jeden punkt procentowy wody po wysuszeniu, ile gramów będą ważyć pomidory? Dla zabawy spróbuj najpierw odgadnąć odpowiedź.
Rozwiązanie Jeden kilogram świeżych pomidorów składa się z \(940\text{g}\) wody i \(60\text{g}\) substancji resztkowych (zwanych suchą masą). Po wysuszeniu do zawartości wody wynoszącej \(93\%\), oznaczmy nieznaną masę pomidora jako \(x\) (w gramach). Ponieważ sucha masa pozostaje w pomidorze, woda w pomidorze waży teraz \(x-60\text{g}\), tj.
\[ \frac{x-60}{x} = \frac{93}{100}, \]
ponieważ stosunek masy wody do masy całkowitej musi wynosić dokładnie \(93/100\). Rozwiązaniem tego równania jest masa pomidorów
\[x=\frac{6000}{7}\doteq 857{.}14\,\text{g}.\]
Ćwiczenie 2. Wyznacz wzór i dziedzinę funkcji opisującej zależność między rzeczywistą masą pomidorów a procentową zawartością wody zawartą w nich podczas suszenia kilograma świeżych pomidorów. Naszkicuj wykres tej funkcji.
Rozwiązanie: Z zadania wiemy, że zmienną niezależną (oznaczaną jak zwykle przez \(x\)) to procentowa zawartość wody w pomidorach, a zmienna zależna (oznaczana przez \(y\)) to rzeczywista waga pomidorów (w gramach). Zatem
\[ \frac{y-60}{y}=\frac{x}{100}. \tag{1} \]
Stąd, wyrażając \(y\), otrzymujemy wzór na pożądaną funkcję \(f\):
\[ f\colon y= -\frac{6000}{x-100}. \]
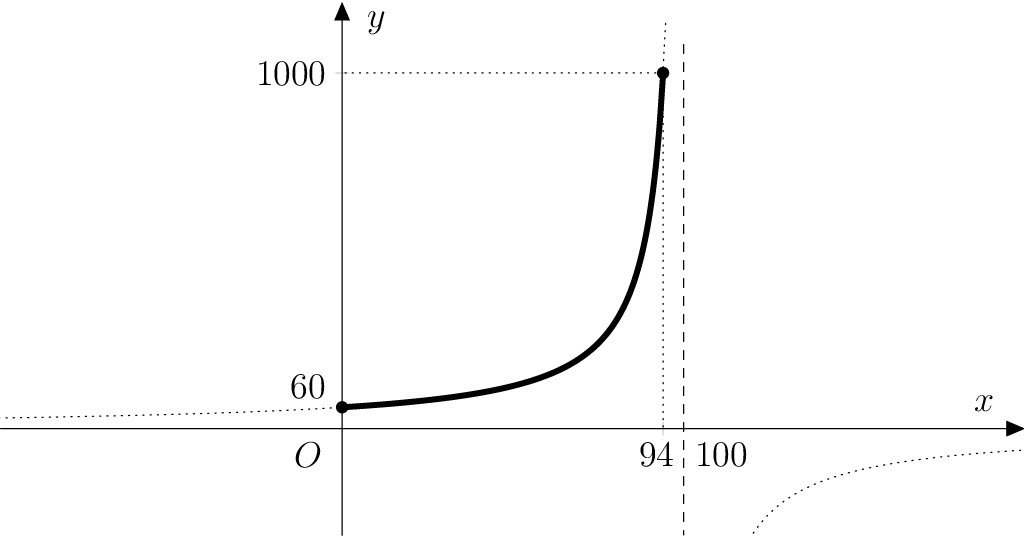
Dziedziną tej funkcji jest zamknięty przedział \(\left\langle 0; 94 \right\rangle\), gdzie wartości graniczne odpowiadają pomidorom całkowicie odwodnionym i świeżym pomidorom o zawartości wody \(94\%\). Wykres funkcji \(f\) leży na hiperboli, która jest przesuniętym wykresem funkcji \(f_0\colon y = -\frac{6000}{x}\) o 100 jednostek w kierunku dodatniej półosi \(x\).
**Ćwiczenie 3. Jak ogólnie zmienia się wzór funkcji z poprzedniego ćwiczenia? jeśli wysuszymy \(m\) gramów świeżych pomidorów?
Rozwiązanie Zacznijmy od równania \((1)\) w rozwiązaniu ćwiczenia 2, gdzie zastępujemy liczbę \(60\) (tj. wagę suchej masy w gramach) ogólnym wyrażeniem \(\frac{6}{100}m\) ,ponieważ sucha masa stanowi \(6\%\) masy świeżych pomidorów. Wyrażając zmienną \(y\), otrzymujemy wzór funkcji \(g\) (z parametrem \(m\)) jako
\[ g\colon y = -\frac{6m}{x-100}. \tag{2} \]
Ćwiczenie 4. Ile kilogramów świeżych pomidorów potrzeba do wyprodukowania
kilograma suszonych pomidorów o zawartości wody wynoszącej \(10\%\);
\(500\,\text{g}\) suszonych pomidorów o zawartości wody \(20\%\);
\(250\,\text{g}\) suszonych pomidorów o zawartości wody \(40\%\)?
Podstawiając kolejno współrzędne tych trzech punktów dla \(x\) i \(y\) do równania \((2)\) i rozwiązując otrzymane równania liniowe, otrzymujemy pierwiastki \(m_1=15\,000\), \(m_2=\frac{20\,000}{3}\) i \(m_3=2500\). Wyniki są zatem następujące \(15\text{kg}\) (dla przypadku a), \(\frac{20}{3}\doteq 6{.}67\text{kg}\) (dla przypadku b) i \(2{.}5\text{kg}\) (dla przypadku c).