Parabolická anténa
 20 min.,
20 min.,  2/3
2/3 Kvalitní anténa je jedním z nejdůležitějších prvků každého radaru. Jedním typem antény je tzv. parabolická anténa. Tato anténa má tvar rotačního paraboloidu (to znamená, že vznikla rotací části paraboly kolem její osy) a slouží nejen k radiolokaci, ale například i k příjmu satelitního televizního vysílání.
Parabolický tvar přijímací antény zajišťuje, že přicházející signály z určitého směru se po odrazu od antény soustřeďují do jednoho bodu, a to do ohniska paraboly, jejíž rotací anténa vznikla. V tomto bodě proto bývá přijímač antény. Pokud je naopak v ohnisku umístěn výstup z vysokofrekvenčního generátoru (zářič), funguje anténa jako vysílací. Energie ze zářiče se po odrazu od paraboloidu soustředí do úzkého proudu mikrovln s rovnoběžnými paprsky.
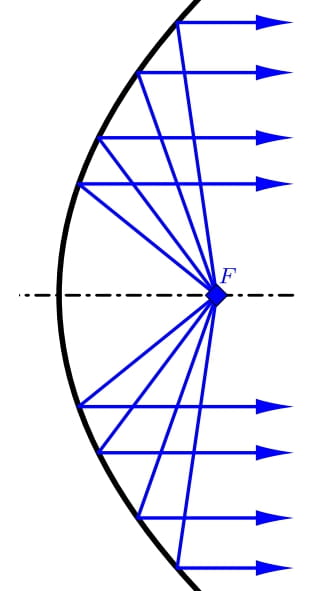
Osovým řezem antény je část paraboly. Ta je charakterizovaná dvěma parametry. Jsou to průměr \(d\) antény a hloubka \(h\) antény, viz obrázek. Tyto dva údaje jsou určující pro polohu ohniska \(F\). Vzdálenost ohniska od vrcholu paraboly označíme \(f\). Poslední důležitou charakteristikou antény je její úhel otevření, který vyjadřuje pod jakým úhlem jsou vidět okraje části paraboly z ohniska. Jeho hodnotu označujeme \(2\varphi\).
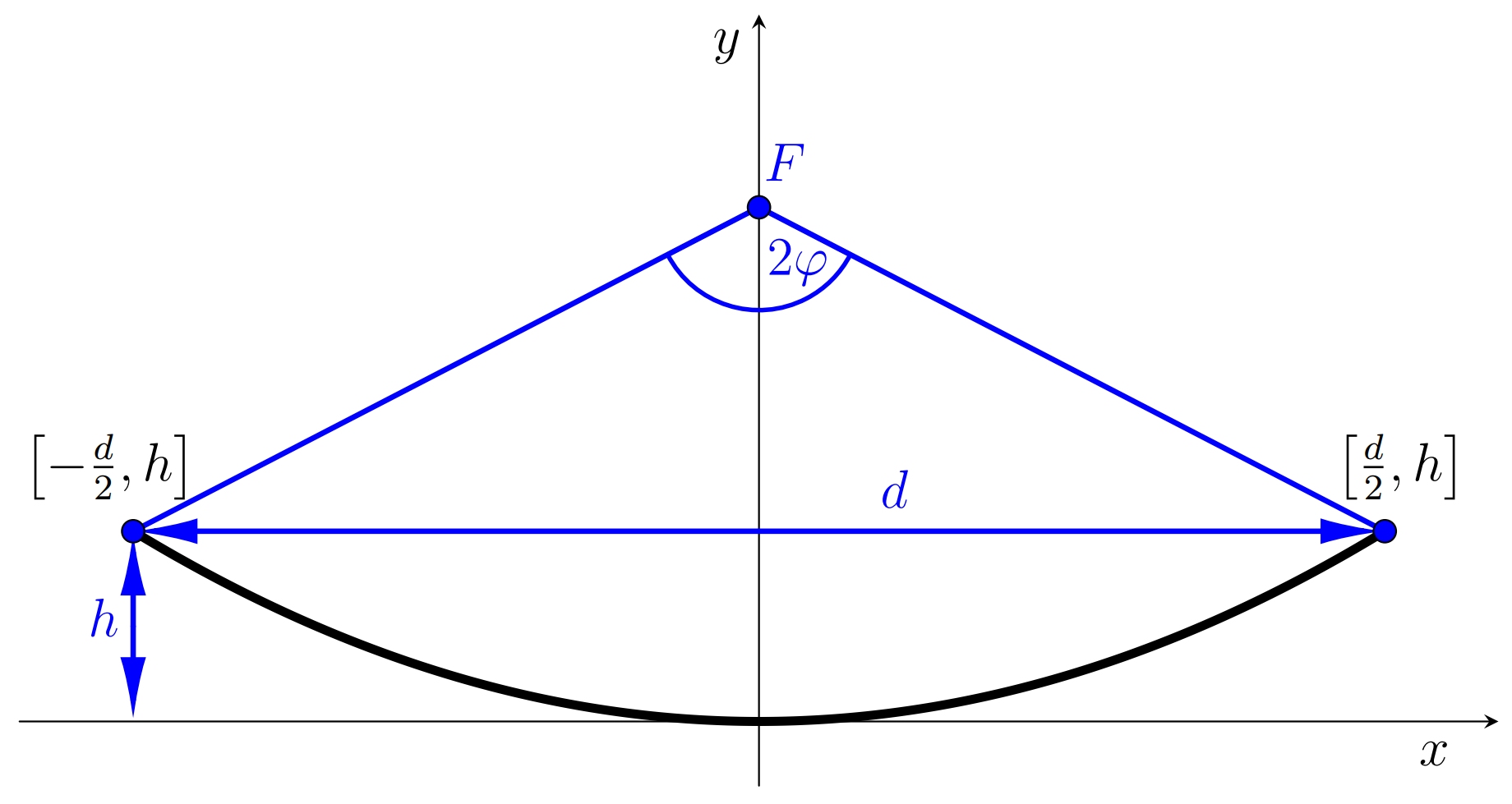
Při výpočtu polohy ohniska je výhodné předpokládat umístění vrcholu paraboly v počátku, kdy osa \(x\) je zároveň tečnou této paraboly v jejím vrcholu. Vrcholová rovnice paraboly je pak \[x^2=2py,\] kde \(p\) je parametr paraboly, tedy vzdálenost ohniska od řídící přímky paraboly. Pro parametr \(p\) platí \(p=2f\).
Zadání
Úloha 1. Máme k dispozici parabolickou anténu s průměrem \(d=120\,\text{cm}\) a hloubkou \(h=20{,}3\,\text{cm}\). Takováto anténa je vhodná pro využití v radioamatérském pásmu \(5{,}76\,\text{GHz}\) (vlnová délka \(5{,}2\,\text{cm}\)). Vypočítejte, kam je nutné umístit přijímač.
Řešení. Aby anténa správně fungovala, musí přijímač ležet v ohnisku parabolické antény. Máme tedy určit polohu ohniska. Vzhledem k umístění paraboly mají krajní body její části souřadnice \(\left[-\frac{d}{2},h\right]\) a \(\left[\frac{d}{2},h\right]\). Navíc oba tyto body musí splňovat vrcholovou rovnici paraboly \(x^2=2py,\) kde parametr \(p\) určuje polohu ohniska, přičemž při našem označení platí \(f=\frac{p}{2}\).
Dosaďme pravý krajní bod do této rovnice a určeme \(p\): \[60^2=2p\cdot 20{,}3.\] Odtud tedy \(p \doteq 88{,}7\,\text{cm}\). Ohnisko leží na ose \(y\) ve vzdálenosti \(f=\frac{p}{2}\doteq44{,}3\,\text{cm}\) od vrcholu paraboly.
Úloha 2. Určete předpis kvadratické funkce (v explicitním tvaru) vyjadřující zakřivení parabolické antény a znázorněte ji (např. v GeoGebře).
Řešení. Z vrcholové rovnice paraboly \(x^2=2\cdot 88{,}7 y\) je nutné vyjádřit souřadnici \(y\). Pro kvadratickou funkci platí \[ y=\frac{1}{177{,}4}x^2. \] Graf kvadratická funkce bude správně zachycovat zakřivení parabolické antény, pokud bude platit, že na obou osách je stejné měřítko.
Úloha 3. Vypočítejte úhel otevření paraboly \(2\varphi\).
Řešení. Pro výpočet otevření paraboly využijeme pravoúhlého trojúhelníka s odvěsnami délky \(f-h\) a \(\frac{d}{2}\).
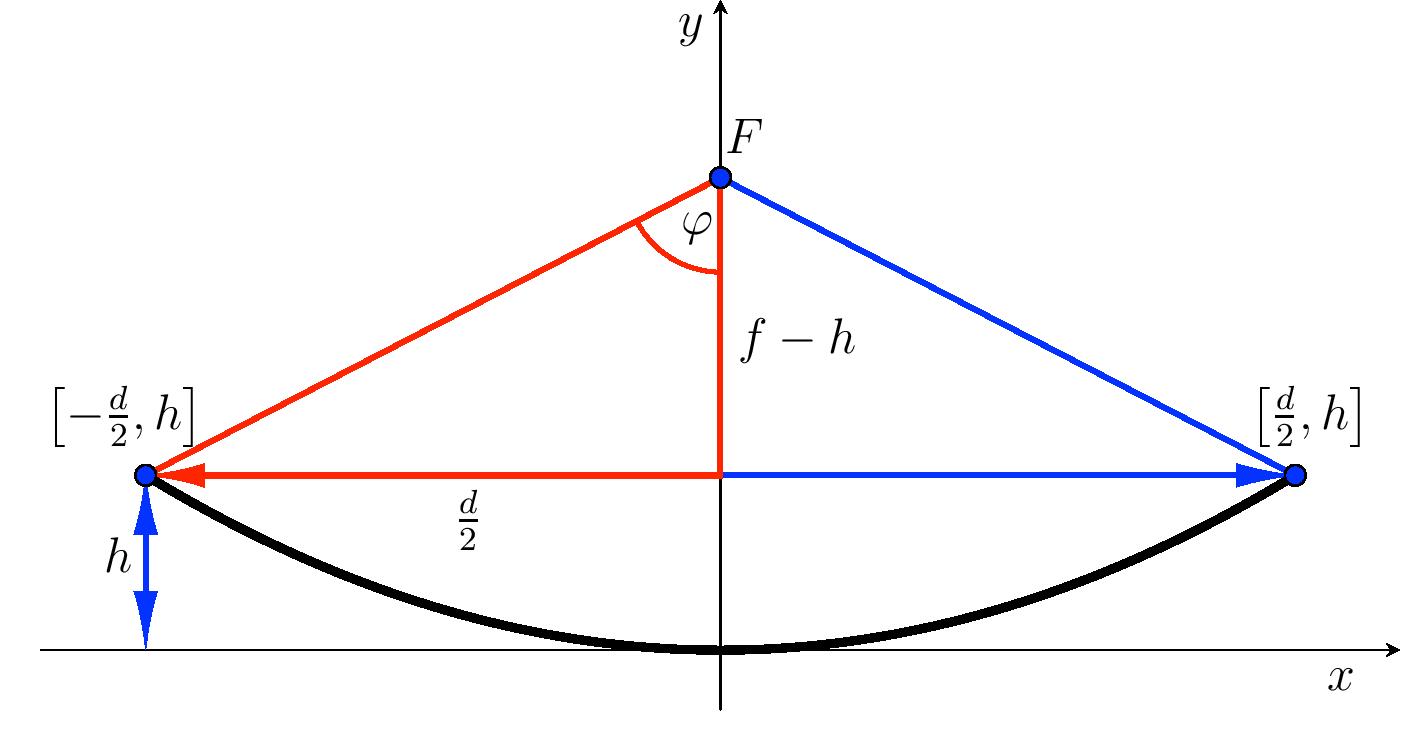
Pro polovinu úhlu otevření platí \[\mathrm{tg}\,\varphi=\frac{\frac{d}{2}}{f-h}=\frac{60}{44{,}3-20{,}3}\quad\Longrightarrow\quad \varphi\doteq 68{,}2^{\circ}.\] Úhel otevření paraboly \(2\varphi\) je \(136{,}4^{\circ}\).
Literatura
- Střihavka, František. Parabolické antény [1994] [online]. Dostupné z https://www.ok2kkw.com/next/ok1ca_1994dish.htm [cit. 30.,10.,2023]
- Kusala, Jaroslav. Radarové antény [online]. Dostupné z https://www.army.cz/images/id_8001_9000/8753/radar/k25.htm [cit. 30.,10.,2023].
- Interactive mathematics. The Parabola [online]. Dostupné z https://www.intmath.com/plane-analytic-geometry/4-parabola.php [cit. 30.,10.,2023].