Dried Tomatoes
 35 min.,
35 min.,  3/3
3/3 Drying is one of the oldest and healthiest methods of long-term food preservation, extending the shelf life of food for up to a year. It is a way to preserve the taste, smell and color of food. Another advantage is that dried foods take up much less space.
It is one of the most commonly used preservation methods both in households and in the processing industry. In households, fruits, vegetables or mushrooms are dried freely in the sun, in an oven, or in a dehydrator. Commercial drying of fruit then takes place in specialized dehydrators.
When drying, it is important that each piece is exposed to a constant flow of warm air, which evaporates the water and lowers the humidity. The humidity should drop to a maximum of \(30\%\). At this humidity, the growth of microorganisms and mold is prevented, regardless of the packaging material and the storage temperature.
Assignment
Tomatoes are one of the typical vegetables that are dried. Some lovers of Italian cuisine consider them a little red miracle. In terms of drying, tomatoes are among the most demanding because they consist of \(94\%\) water.
All percentages in the following exercises are expressing mass fractions, i.e. they numerically represent the number of grams of the component in \(100\,\text{g}\) of mass.
Exercise 1. If a kilogram of fresh tomatoes loses one percentage point of water after drying, how many grams will the tomatoes weigh? Just for fun, try guessing the answer first.
Solution. One kilogram of fresh tomatoes is made up of \(940\,\text{g}\) of water and \(60\,\text{g}\) of residual substances (called dry matter). After drying to a water content of \(93\%\), let us denote the unknown mass of the tomato as \(x\) (in grams). Since the dry matter remains in the tomato, the water in the tomato now weighs \(x-60\,\text{g}\), i.e. \[ \frac{x-60}{x} = \frac{93}{100}, \] since the ratio of the weight of the water to the total weight must be exactly \(93/100\). The solution to this equation is the mass of the tomatoes \[x=\frac{6000}{7}\doteq 857{.}14\,\text{g}.\]
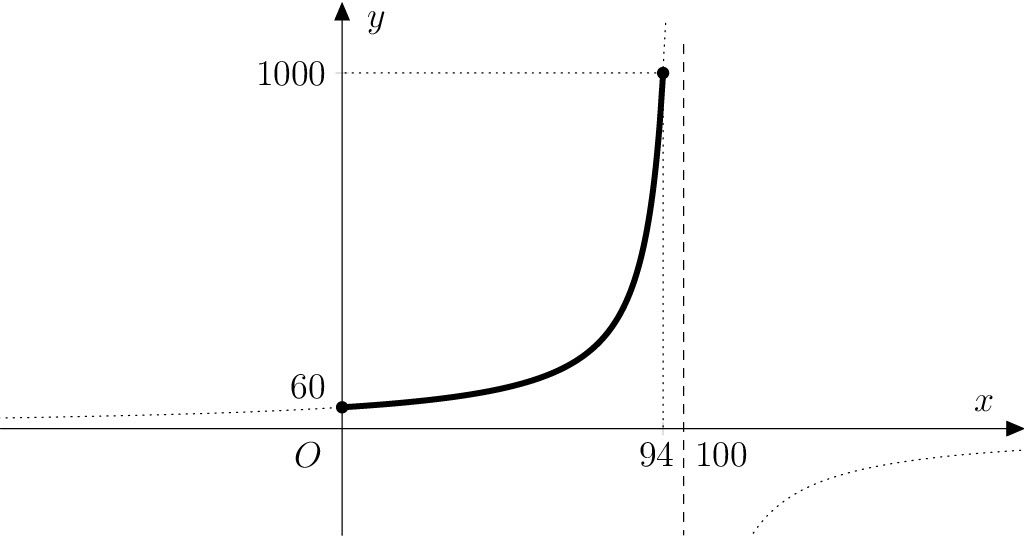
Exercise 2. Determine the formula and the domain of a function that describes the relationship between the actual weight of the tomatoes and the percentage of water contained in them during the drying of one kilogram of fresh tomatoes. Sketch the graph of this function.
Solution. We know from the assignment that the independent variable (denoted as usual by \(x\)) is the percentage of water in the tomatoes, and the dependent variable (denoted by \(y\)) is the actual weight of the tomatoes (in grams). Thus \[ \frac{y-60}{y}=\frac{x}{100}. \tag{1} \] From here, by expressing \(y\), we get the formula for the desired function \(f\): \[ f\colon y= -\frac{6000}{x-100}. \]
The domain of this function is the closed interval \(\left\langle 0; 94 \right\rangle\), where boundary values correspond to tomatoes completely dehydrated and fresh tomatoes with a water content of \(94\%\). The graph of the function \(f\) lies on a hyperbola, which is a shifted graph of the function \(f_0\colon y = -\frac{6000}{x}\) by 100 units in the direction of the positive semi-axis \(x\).
Exercise 3. In general, how does the formula of the function from the previous exercise change if we dry \(m\) grams of fresh tomatoes?
Solution. Let us begin with equation \((1)\) in the solution of Exercise 2, where we replace the number \(60\) (i.e. the weight of the dry matter in grams) by the general expression \(\frac{6}{100}m\), because the dry matter makes up \(6\%\) of the weight of fresh tomatoes. By expressing the variable \(y\), we get the formula of the function \(g\) (with parameter \(m\)) as
\[ g\colon y = -\frac{6m}{x-100}. \tag{2} \]
Exercise 4. How many kilograms of fresh tomatoes are needed to make
- one kilogram of dried tomatoes with a water content of \(10\%\);
- \(500\,\text{g}\) of dried tomatoes with \(20\%\) water content;
- \(250\,\text{g}\) of dried tomatoes with \(40\%\) water content?
Solution. If we refer to the function \(g\) from the solution of Exercise 3, we ask for which \(m\) the graph of the function \(g\) passes through a point with coordinates \([10;1000]\) (in case a), or through a point with coordinates \([20;500]\) (in case b), or through point \([40;250]\) (in case c).
By successively substituting the coordinates of those three points for \(x\) and \(y\) into equation \((2)\) and solving the resulting linear equations, we obtain the roots \(m_1=15\,000\), \(m_2=\frac{20\,000}{3}\) and \(m_3=2500\). The results are therefore \(15\,\text{kg}\) (for case a), \(\frac{20}{3}\doteq 6{.}67\,\text{kg}\) (for case b) and \(2{.}5\,\text{kg}\) (for case c).
Literature
- Richtrmocová, Barbora. Zdravotní a nutriční aspekty sušeného ovoce. Bakalářská práce. Masarykova univerzita, 2018.