Parabolická kalkulačka

Pri surfovaní na internete našla Eva zaujímavý fakt o grafe funkcie \(f\colon y = x^2\), ktorý môže slúžiť ako kalkulačka na násobenie dvoch čísel \(a\) a \(b\).¹ Postup je nasledovný:

1. Na osi \(x\) vyznačime obrazy čísel \(-a\) a \(b\).
2. V týchto bodoch zostrojíme priamky kolmé na os \(x\), ktoré sa pretnú s grafom funkcie \(f\) a vzniknú priesečníky.
3. Priamka prechádzajúca novovytvorenými priesečníkmi pretína os \(y\) v bode, ktorého vzdialenosť od počiatku súradného systému je \(ab\).

Tento postup si môžete vyskúšať v priloženom pracovnom liste, jeho ilustrácia je tiež možná v GeoGebre. Interaktívny applet nájdete na webovej stránke https://www.geogebra.org/m/sj5cjbaf.

Riešenie. Z postupu je zrejmé, že ak obrazy čísel \(-a\) a \(b\) splynú, priamku opísanú v treťom kroku nemožno jednoznačne zostrojiť. Preto daný postup nefunguje, ak platí \(-a=b\). Ukážeme, že okrem tohto prípadu platí postup pre všetky ostatné dvojice čísel \(a\) a \(b\). Podľa postupu zo zadania zostrojme na osi \(x\) body zodpovedajúce číslam \(-a\) a \(b\) , a potom v týchto bodoch zostrojme kolmice na os \(x\). Priesečníky týchto kolmíc s parabolou označme ako \(A\) a \(B\) a priamku \(AB\) potom označime ako \(p\). Priamka \(p\) pretína os \(y\) v bode \(C\), ktorý určuje neznáme číslo \(m\).

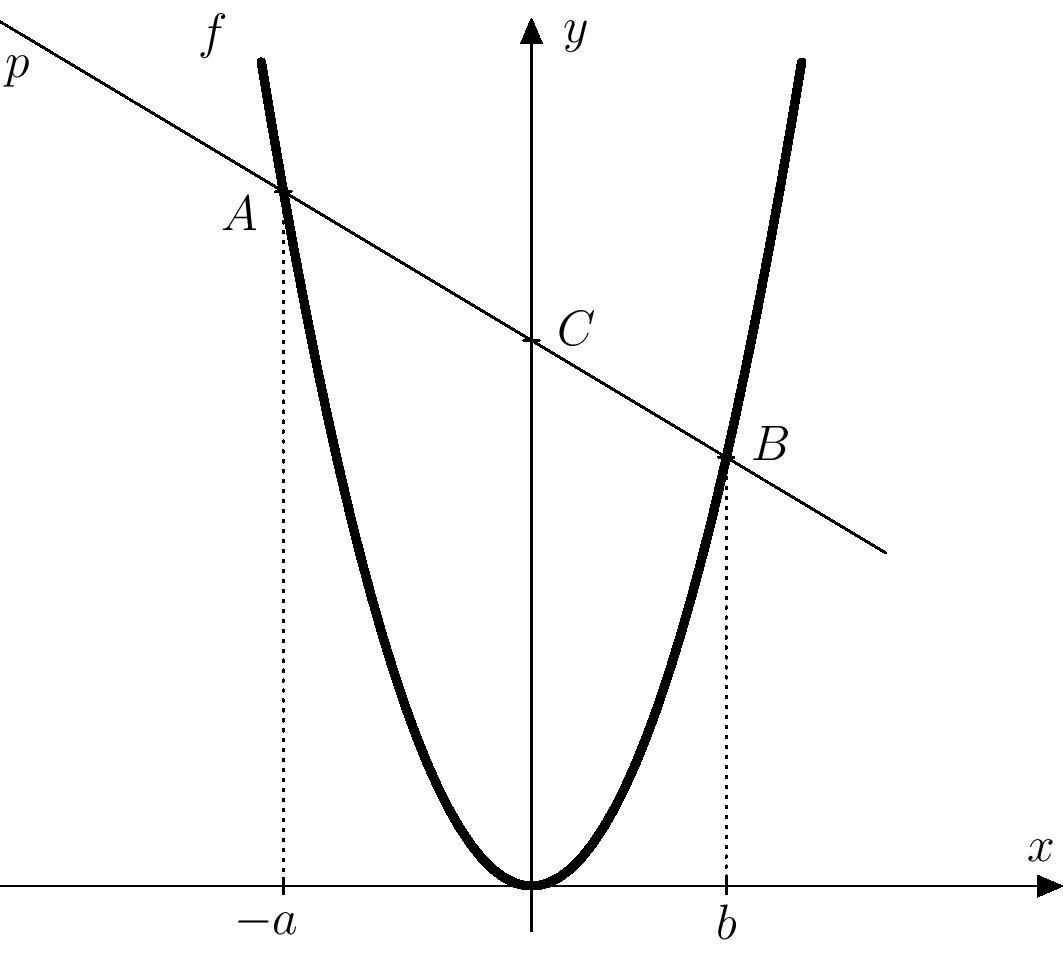
Priamka \(p\) je definovaná dvoma bodmi \(A(-a;a^2)\) a \(B(b;b^2)\), a teda smerový vektor je \[\overrightarrow{u}=\overrightarrow{AB}= [b+a; b^2-a^2].\] Vynásobením vektora \(\overrightarrow{u}\) číslom \(\frac{1}{a+b}\) dostaneme \[\overrightarrow{u}=[1; b-a].\] Túto úpravu môžeme vykonať, pretože v našom prípade \(b\neq a\) a tiež \(b+a\neq0\). Dostávame tak parametrické rovnice \[ \begin{aligned} p\colon X &= B + t\cdot\overrightarrow{u}, t\in\mathbb{R}\\[2mm] p\colon x &= b + t \\ y &= b^2 + t\cdot (b-a), t\in\mathbb{R} \end{aligned} \]

Dosadením súradníc bodu \(C\) do ľavých strán rovníc (t. j. \(x=0\), \(y=m\)) dostaneme sústavu rovníc \[ \begin{aligned} 0 &= b+t\\ m &= b^2+t(b-a) \end{aligned} \] Z prvej rovnice vyjadríme \(t=-b\) a dosadíme do druhej rovnice. Odtiaľ \[ \begin{aligned} m &=b^2+(-b)\cdot(b-a) \\ m &=ab. \end{aligned} \] Toto je výsledok, ktorý sme potrebovali dokázať.