Parabolic calculator

While surfing the Internet, Eva found an interesting fact about the graph of a function \(f\colon y = x^2\) which is that the graph can be used as a calculator to multiply two numbers \(a\) and \(b\).¹ The procedure is as follows:

1. On the \(x\)-axis mark the points corresponding to the numbers \(-a\) and \(b\).
2. At these points, draw lines perpendicular to the \(x\)-axis and construct their intersections with the graph of the function \(f\).
3. The line passing through the newly constructed intersections intersects the \(y\)-axis at a point whose distance from the origin is \(ab\).

You can try the procedure in the attached worksheet, its illustrations is also available in GeoGebra. The interactive applet can be found on the website https://www.geogebra.org/m/sj5cjbaf.

Solution. It is evident from the procedure that if the images of the numbers \(-a\) and \(b\) merge, the line described in the third step cannot be uniquely constructed. Therefore, the given procedure will not work if \(-a=b\) holds. We will show that, besides this case, the procedure holds for all other pairs of numbers \(a\) and \(b\).

Let’s construct, according to the given procedure, on the \(x\)-axis the points corresponding to the numbers \(-a\) and \(b\), and then construct perpendiculars at these points to the \(x\)-axis. Let’s denote the intersections of these perpendiculars with the parabola by \(A\) and \(B\), and let the line \(AB\) be denoted by \(p\). The line \(p\) intersects the \(y\) axis at the point \(C\), which determines the unknown number \(m\).

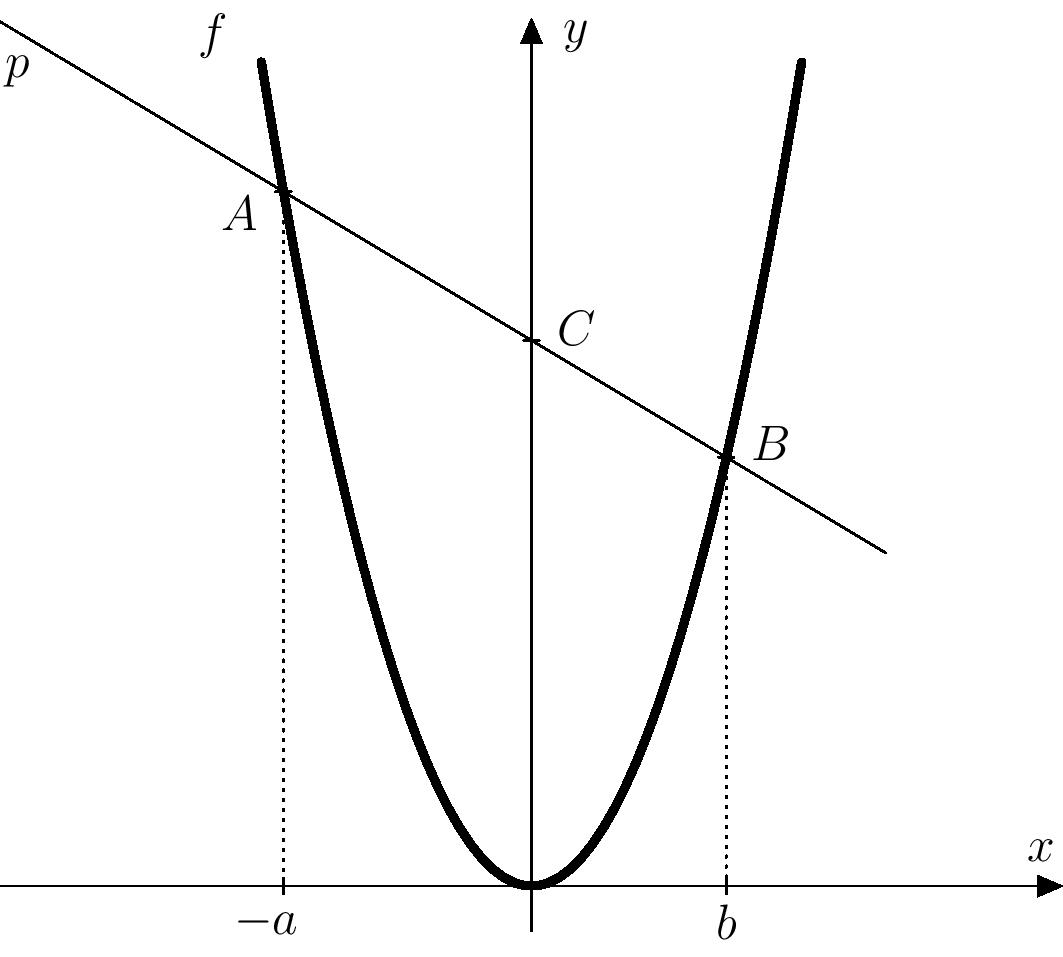
The line \(p\) is defined by the points \(A(-a;a^2)\) and \(B(b;b^2)\), so the direction vector is \[\overrightarrow{u}=\overrightarrow{AB}= [b+a; b^2-a^2].\] By multiplying the vector \(\overrightarrow{u}\) with the number \(\frac{1}{a+b}\) we get \[\overrightarrow{u}=[1; b-a].\] This adjustment can be made since in our case is \(b\neq a\), and so \(b+a\neq0\). Thus, we get the parametric equations \[ \begin{aligned} p\colon X &= B + t\cdot\overrightarrow{u}, t\in\mathbb{R}\\[2mm] p\colon x &= b + t \\ y &= b^2 + t\cdot (b-a), t\in\mathbb{R} \end{aligned} \]

By substituting the coordinates of point \(C\) into the left sides of the equations (i.e. \(x=0\), \(y=m\)) we get the system \[ \begin{aligned} 0 &= b+t\\ m &= b^2+t(b-a) \end{aligned} \] From the first equation, we express \(t=-b\) and substitute it into the second equation. From here \[ \begin{aligned} m &=b^2+(-b)\cdot(b-a) \\ m &=ab. \end{aligned} \] This is the result we needed to prove.