Parabolická kalkulačka

Eva našla při surfování na internetu jednu zajímavost týkající se grafu funkce \(f\colon y = x^2\), který může posloužit jako kalkulačka k vynásobení dvou čísel \(a\) a \(b\).¹ Postup je následující:

1. Na ose \(x\) se vyznačí obrazy čísel \(-a\) a \(b\).
2. V těchto bodech se vztyčí kolmice k ose \(x\) a sestrojí se její průsečíky s grafem funkce \(f\).
3. Přímka procházející právě sestrojenými průsečíky protne osu \(y\) v bodě, jehož vzdálenost od počátku je \(ab\).

Uvedený postup si můžete vyzkoušet v přiloženém pracovním listu, jeho ilustrace je možná také v GeoGebře. Interaktivní applet najdete na stránkách https://www.geogebra.org/m/sj5cjbaf.

Řešení. Z postupu je patrné, že jestliže obrazy čísel \(-a\) a \(b\) splynou, přímku popisovanou ve třetím bodě nebude možné jednoznačně sestrojit. Uvedený postup proto nebude fungovat, bude-li platit \(-a=b\). Ukážeme, že kromě tohoto případu platí postup pro všechny ostatní dvojice čísel \(a\) a \(b\).

Sestrojme na ose \(x\) dle postupu ze zadání obraz čísla \(-a\) a \(b\) a dále vztyčme v těchto bodech kolmice k ose \(x\). Průsečíky těchto kolmic s parabolou označme \(A\) a \(B\), přímku \(AB\) pak označme jako \(p\). Přímka \(p\) protíná osu \(y\) v bodě \(C\), který určuje neznámé číslo \(m\).

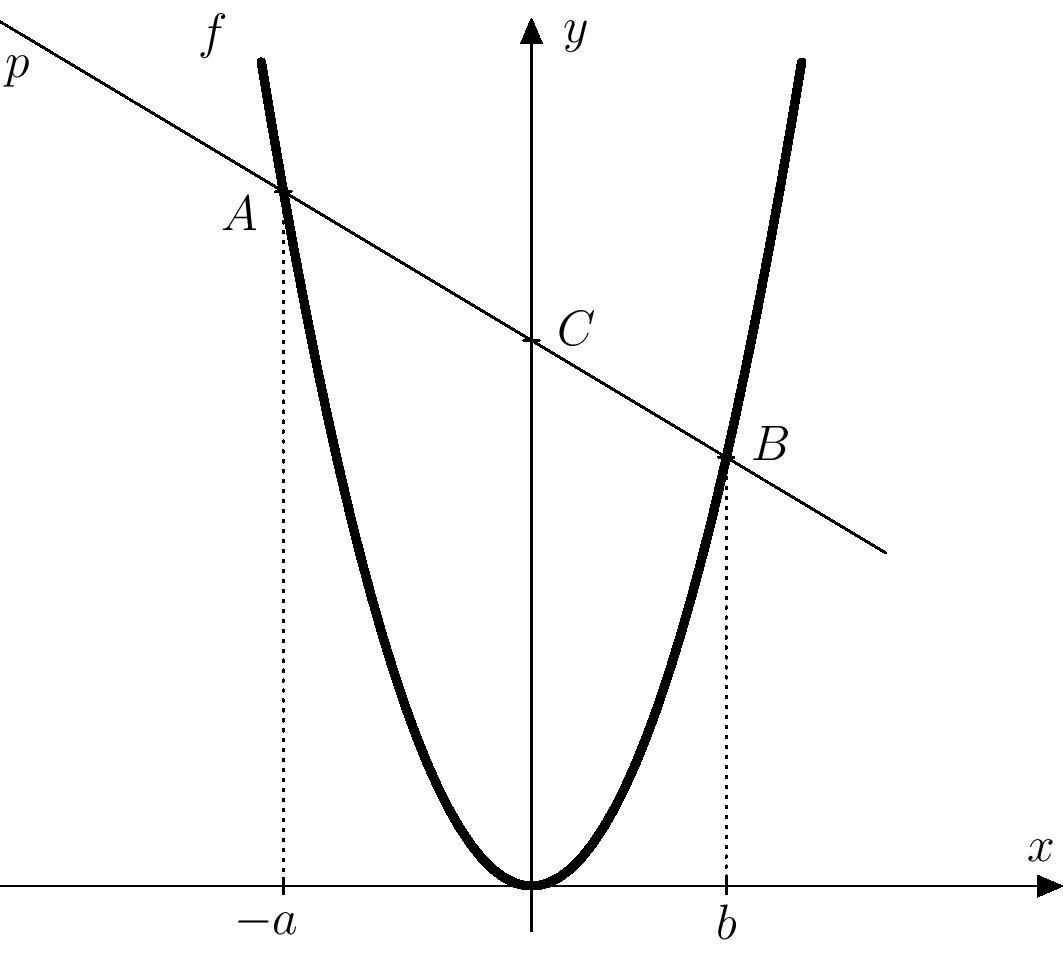
Přímka \(p\) je dána dvěma body \(A[-a;a^2]\) a \(B[b;b^2]\), tedy směrový vektor je \[\overrightarrow{u}=\overrightarrow{AB}= (b+a; b^2-a^2).\] Vynásobením vektoru \(\overrightarrow{u}\) číslem \(\frac{1}{a+b}\) dostaneme \[\overrightarrow{u}=(1; b-a).\] Tuto úpravu je možné provést, neboť pro náš případ \(b\neq a\) je \(b+a\neq0\). Dostáváme tak parametrické rovnice

\[ \begin{aligned} p\colon X &= B + t\cdot\overrightarrow{u}, t\in\mathbb{R}\\ p\colon x &= b + t \\ y &= b^2 + t\cdot (b-a), t\in\mathbb{R} \end{aligned} \]

Dosazením souřadnic bodu \(C\) do levých stran rovnic (tj. \(x=0\), \(y=m\)) dostaneme soustavu

\[ \begin{aligned} 0 &= b+t\\ m &= b^2+t(b-a) \end{aligned} \]

Z první rovnice vyjádříme \(t=-b\) a dosadíme do druhé rovnice. Odsud

\[ \begin{aligned} m &=b^2+(-b)\cdot(b-a) \\ m &=ab, \end{aligned} \]

což jsme měli dokázat.