Kalkulator paraboliczny

Podczas surfowania po Internecie Eva znalazła interesujący fakt dotyczący wykresu funkcji \(f\colon y = x^2\), który polega na tym, że wykres może być użyty jako kalkulator do pomnożenia dwóch liczb \(a\) i \(b\).¹ Procedura jest następująca:

1. Na osi \(x\) zaznacz punkty odpowiadające liczbom \(-a\) i \(b\).
2. W tych punktach narysuj linie prostopadłe do osi \(x\) i skonstruuj skonstruować ich przecięcia z wykresem funkcji \(f\).
3. Linia przechodząca przez nowo skonstruowane punkty przecięcia przecina oś \(y\) w punkcie, którego odległość od od początku wynosi \(ab\).

Procedurę można wypróbować w załączonym arkuszu, jego ilustracje są również dostępne w programie GeoGebra. Interaktywny aplet można znaleźć na stronie internetowej https://www.geogebra.org/m/sj5cjbaf.

Rozwiązanie. Z procedury wynika, że jeśli obrazy liczb \(-a\) i \(b\) łączą się, linia opisana w trzecim kroku nie może być jednoznacznie skonstruowana. Dlatego podana procedura nie zadziała, jeśli \(-a=b\). My pokażemy, że poza tym przypadkiem, procedura działa dla wszystkich innych par liczb \(a\) i \(b\).

Skonstruujmy, zgodnie z podaną procedurą, na osi \(x\) punkty odpowiadające liczbom \(-a\) i \(-b\), a następnie skonstruujmy w tych punktach proste prostopadłe do osi \(x\). Oznaczmy przecięcia tych prostopadłych z parabolą przez \(A\) i \(B\), a linię prostą \(AB\) oznaczmy przez \(p\). Prosta \(p\) przecina oś \(y\) w punkcie \(C\), który wyznacza nieznaną liczbę \(m\).

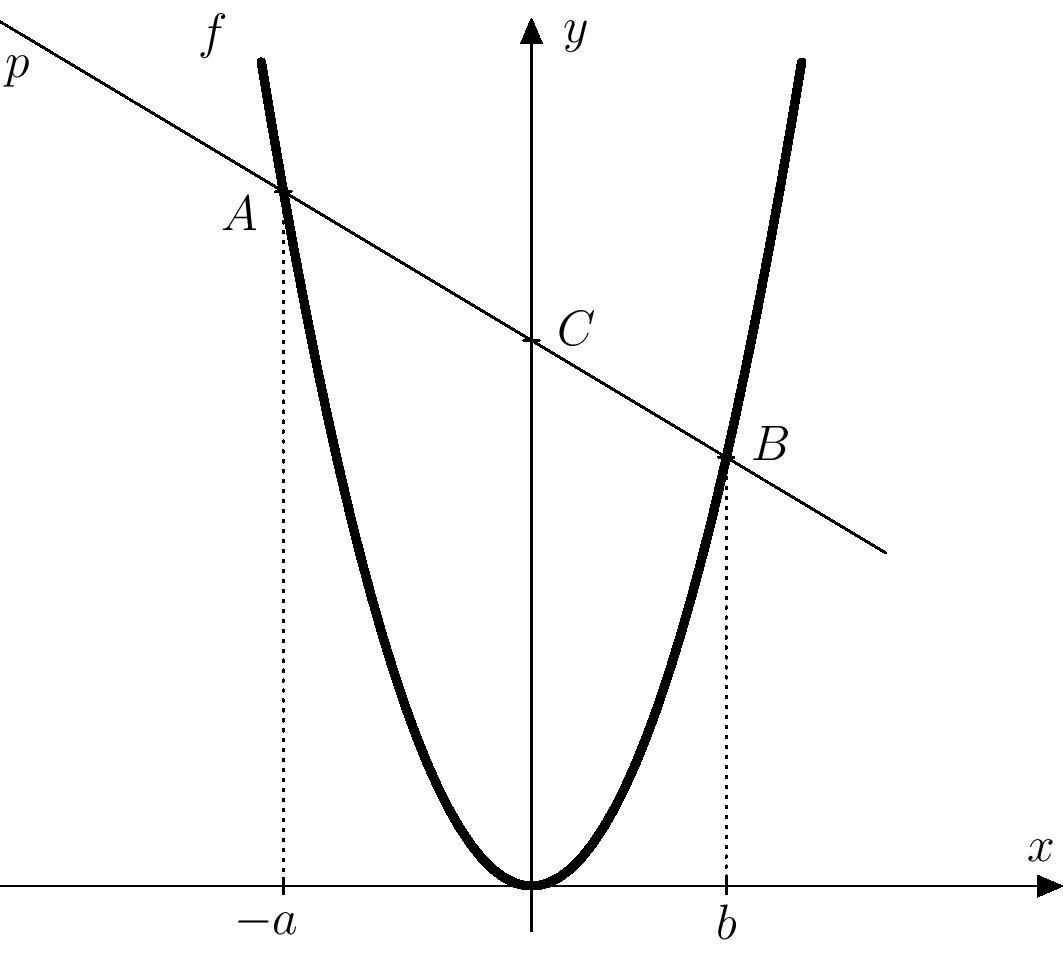
Prosta \(p\) jest określona przez punkty \(A(-a;a^2)\) i \(B(b;b^2)\), więc wektor kierunku to \[\overrightarrow{u}=\overrightarrow{AB}= [b+a; b^2-a^2].\] Mnożąc wektor \(\overrightarrow{u}\) przez liczbę \(\frac{1}{a+b}\) otrzymujemy \[\overrightarrow{u}=[1; b-a].\] Korektę tę można wykonać, ponieważ w naszym przypadku \(b\neq a\), a więc \(b+a\neq0\). W ten sposób otrzymujemy równania parametryczne

\[ \begin{aligned} p\colon X &= B + t\cdot\overrightarrow{u}, t\in\mathbb{R}\\ p\colon x &= b + t \\ y &= b^2 + t\cdot (b-a), t\in\mathbb{R} \end{aligned} \]

Podstawiając współrzędne punktu \(C\) po lewej stronie równań (tj. \(x=0\), \(y=m\)) otrzymujemy układ

\[ \begin{aligned} 0 &= b+t\\ m &= b^2+t(b-a) \end{aligned} \]

Z pierwszego równania mamy \(t=-b\) i podstawiamy je do drugiego równania. Stąd

\[ \begin{aligned} m &=b^2+(-b)\cdot(b-a) \\ m &=ab. \end{aligned} \]

Jest to wynik, który musieliśmy udowodnić.