Calculadora de parábola

Navegando por Internet, Eva ha encontrado un dato interesante sobre la gráfica de una función \(f\colon y = x^2\) y es que la gráfica se puede utilizar como calculadora para multiplicar dos números \(a\) y \(b\).¹ El procedimiento es el siguiente:

1. En el eje \(x\) marca los puntos correspondientes a los números \(-a\) y \(b\).
2. En estos puntos, traza rectas perpendiculares al eje \(x\) y construye sus intersecciones con la gráfica de la función \(f\).
3. La recta que pasa por las intersecciones recién construidas interseca al eje \(y\) en un punto cuya distancia al origen es \(ab\).

Puedes probar el procedimiento en la hoja de trabajo adjunta, sus ilustraciones también están disponibles en GeoGebra. El applet interactivo se encuentra en el sitio web: https://www.geogebra.org/m/sj5cjbaf.

Solución. Del procedimiento se deduce que si las imágenes de los números \(-a\) y $b se fusionan, la recta descrita en el tercer paso no se puede construir de forma única. Por lo tanto, el procedimiento dado no funcionará si \(-a=b\) se cumple. Demostraremos que, además de este caso, el procedimiento es válido para todos los demás pares de números \(a\) y \(b\).

Construyamos, según el procedimiento dado, en el eje \(x\) los puntos correspondientes a los números \(-a\) y \(-b\), y luego construyamos perpendiculares en estos puntos al eje \(x\). Denotamos las intersecciones de estas perpendiculares con la parábola por \(A\) y \(B\), y la recta \(AB\) por \(p\). La recta \(p\) corta al eje \(y\) en el punto \(C\), que determina la incógnita \(m\).

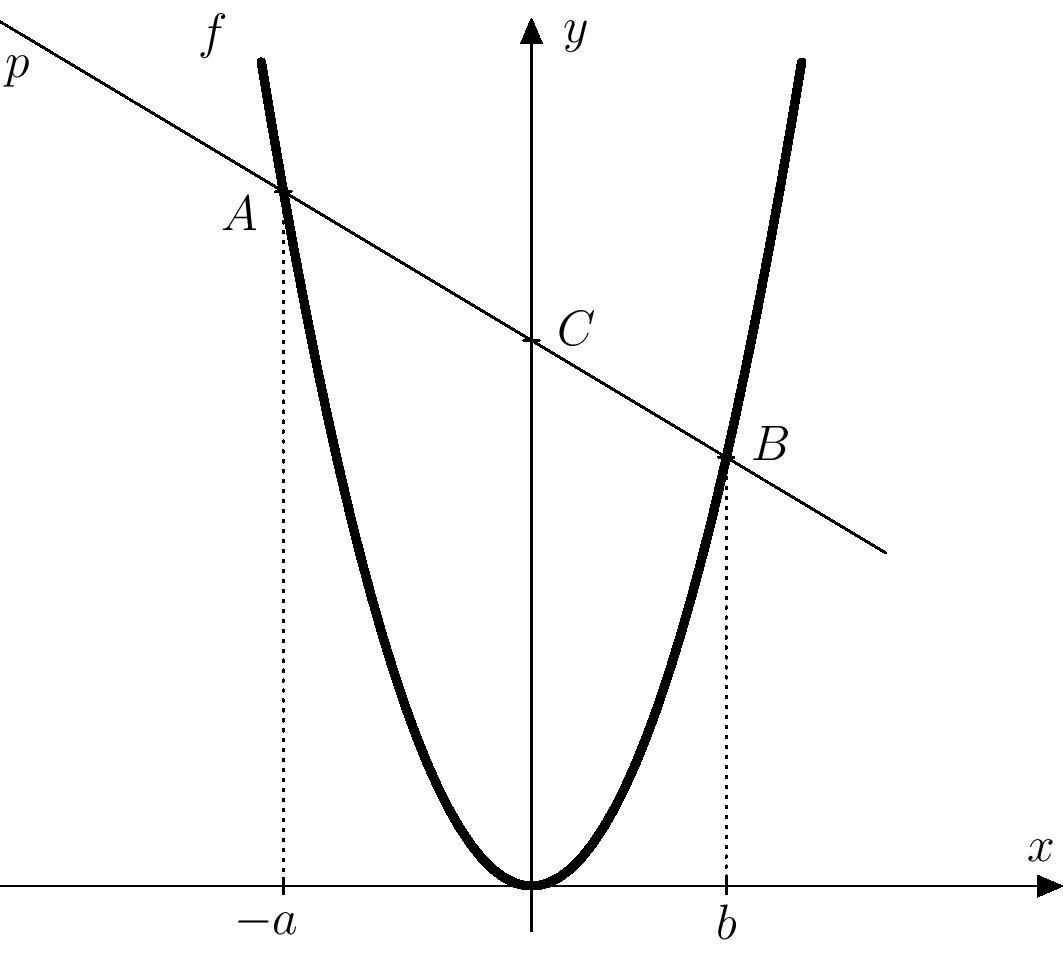
La recta \(p\) está definida por los puntos \(A(-a;a^2)\) y \(B(b;b^2)\), por lo que el vector de dirección es \[\overrightarrow{u}=\overrightarrow{AB}= [b+a; b^2-a^2].\] Multiplicando el vector \(\overrightarrow{u}\) por el número \(\frac{1}{a+b}\) obtenemos \[\overrightarrow{u}=[1; b-a].\] Este ajuste se puede hacer ya que en nuestro caso es \(b\neq a\), y por tanto \(b+a\neq0\). Así, obtenemos las ecuaciones paramétricas \[ \begin{aligned} p\colon X &= B + t\cdot\overrightarrow{u}, t\in\mathbb{R}\\[2mm] p\colon x &= b + t \\ y &= b^2 + t\cdot (b-a), t\in\mathbb{R} \end{aligned} \]

Sustituyendo las coordenadas del punto \(C\) en los lados izquierdos de las ecuaciones (es decir, \(x=0\), \(y=m\)) obtenemos el sistema \[ \begin{aligned} 0 &= b+t\\ m &= b^2+t(b-a) \end{aligned} \] A partir de la primera ecuación, expresamos \(t=-b\) y la sustituimos en la segunda ecuación. A partir de aquí \[ \begin{aligned} m &=b^2+(-b)\cdot(b-a) \\ m &=ab. \end{aligned} \] Este es el resultado que necesitábamos demostrar.