Prievozník sa musí dostať zo svojho doku na jednom brehu rieky do druhého, ktorý sa nachádza na opačnej strane rieky \(500\ \text{m}\) po prúde. Rieka je medzi brehmi priama a široká \(100\ \text{m}\). Rýchlosť prúdu je \(2\ \text{m}/\text{s}\). Taktiež vieme, že prievozníkova loď pláva vzhľadom na vodu rýchlosťou \(12\text{km}/\text{h}\).
Úloha 1. Prievozník sa chce dostať priamo z jedného doku na brehu rieky na druhý. Podarí sa mu to, ak loď nasmeruje pod určitým uhlom a bude tento smer udržiavať. O aký uhol by mal prievozník stočiť svoju loď, aby išiel priamo do druhého doku na opačnom brehu rieky?
Riešenie. Označme bodmi \(A\) a \(B\) východiskový a cieľový bod. Následne bod \(P\) ako pätu kolmice z bodu \(B\) na opačný breh rieky. Označme tiež vektory rýchlosti prúdu, rýchlosti lode vzhľadom na vodu a výslednej rýchlosti lode (rýchlosti lode voči zemskému povrchu) pričom všetky majú začiatočné body v bode \(A\) a koncové body určené nasledovne (pozri obrázok):
Pričom platí,že \(K\in AB\) a podľa pravidla pre sčítanie vektorov je štvoruholník \(MALK\) rovnobežník. Našou úlohou je určiť uhol \(KAL\), ktorý označíme \(\alpha\).
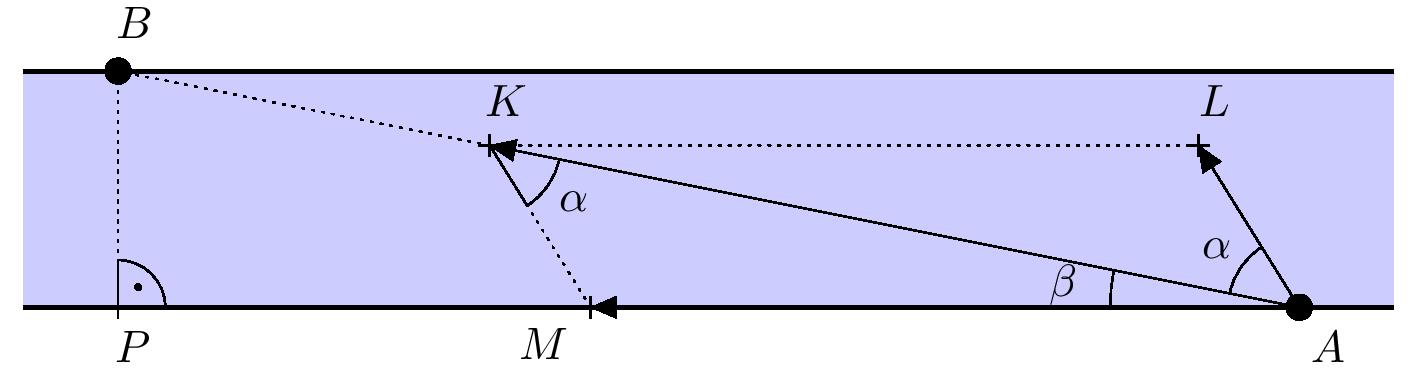
Označme ďalej \(\lvert \sphericalangle MAK \rvert = \beta\), potom \(\lvert \sphericalangle MAL \rvert = \alpha + \beta\). Zo zadania vieme \(|BP|=100\ \text{m}\) a \(|AP|=500\ \text{m}\). Využitím funkcie tangens v pravouhlom trojuholníku \(PAB\) dostaneme \(\beta = \arctan\frac{1}{5} \approx 11^{\circ}19'\).
Každý rovnobežník je rozdelený svojou uhlopriečkou na dva zhodné trojuholníky, preto platí \(\lvert \sphericalangle AKM \rvert= \lvert \sphericalangle KAL \rvert = \alpha\). K výpočtu \(\alpha\) využijeme sínusovú vetu v trojuholníku \(AKM\). Po prevode dĺžok strán na rovnaké jednotky (v našom prípade kilometre), dostaneme konkrétne \(|KM|=12\ \text{km}\) a \(|AM|=2\cdot 3,6=7,2\ \text{km}\). Vyjadríme teraz \(\alpha\) zo sínusovej vety: \[ \begin{aligned} \frac{|KM|}{\sin \beta} &= \frac{|AM|}{\sin \alpha}\\[2mm] \sin \alpha &= \frac{|AM|}{|KM|}\cdot \sin\beta \qquad \Rightarrow \qquad \alpha = \arcsin \left( \frac{|AM|}{|KM|}\cdot \sin\beta \right) \end{aligned} \] Po dosazení konkrétnych hodnôt dostáváme \(\alpha \approx 6^{\circ}45'\). Preto musí prievozník otočiť svoju loď približne o \(7^{\circ}\) doprava od priameho smeru k cieľu.
Úloha 2. Ak digitálne hodiny na lodi ukazujú 11:00 v momente odchodu (nezobrazujú sekundy), aký čas budú hodiny ukazovať, keď loď dorazí do druhého doku?
Riešenie. Najprv určme vzdialenosť medzi dvoma dokmi pomocou Pytagorovej vety v pravouhlom trojuholníku \(ABP\):
\[ \begin{aligned} |AB| &= \sqrt{|AP|^2 + |BP|^2}\\ |AB| &= \sqrt{0,5^2 + 0,1^2}\\ |AB| &\approx 0,51\ \text{km}. \end{aligned} \]
Teraz musíme určit rýchlosť lode vzhľadom k zemskému povrchu, ktorá sa rovná dĺžke úsečky \(AK\). Môžeme ju určit napríklad pomocou kosínusovej vety v trojuholníku \(AKM\). Vnútorný uhol \(\lvert \sphericalangle AMK \rvert =\gamma\) má veľkosť \(180^{\circ}-\alpha - \beta \approx 161^{\circ}56'\). Teraz pre \(|AK|\) môžme zapísať: \[ \begin{aligned} |AK| &= \sqrt{|KM|^2 + |AM|^2 - 2\cdot |KM| \cdot |AM| \cdot \cos \gamma}\\ |AK| &= \sqrt{12^2 + 2^2 - 2\cdot 12 \cdot 2 \cdot \cos(161^{\circ}56')}\\ |AK| &\approx 19,0\ \text{km} \end{aligned} \]
Loď tak prejde dráhu \(0,51\ \text{km}\) priemernou rýchlosťou \(19\ \text{km}/\text{h}\). Výpočtom: \[ \begin{aligned} t &= \frac{\text{s}}{\text{v}}\\ t &= \frac{0,51}{19}\ \text{h}\\ \end{aligned} \] zistíme, že to bude približne 97 sekúnd. Preto budú po príchode do cieľa hodiny ukazovať 11:01 alebo 11:02.