Prom musi dostać się ze swojej przystani na jednym brzegu rzeki do drugiej, która znajduje się na przeciwległym brzegu, \(500 \text{m}\) w dół rzeki. Rzeka między dokami jest prosta i \(100 \text{m}\) szeroka. Prędkość prądu wynosi \(2\text{m}/\text{s}\). Wiemy również, że łódź przewoźnika porusza się z prędkością \(12\ \text{km}/\text{h}\) względem wody.
Zadanie 1. Prom chce przepłynąć bezpośrednio z jednego doku do drugiego. Może to osiągnąć, ustawiając łódź pod kątem w poprzek rzeki i utrzymując ten kierunek. O jaki kąt powinien zawrócić prom, aby popłynąć prosto do drugiego doku?
Rozwiązanie. Oznaczmy przez \(A\) i \(B\) punkt początkowy i docelowy. Oznaczmy również przez \(P\) podnóże linii prostopadłej z punktu \(B\) do przeciwległego brzegu rzeki. Następnie zaznaczamy wektory prędkości prądu, prędkości łodzi względem wody, oraz wynikową prędkość łodzi (prędkość łodzi względem dna rzeki), wszystkie z ich punktami początkowymi w punkcie A i punktami końcowymi w następujący sposób (patrz rysunek):
Ponieważ \(K\in AB\), naszym zadaniem jest określenie kąta \(KAL\), który oznaczymy przez \(alfa\). Zgodnie z regułą dodawania wektorów czworokąt \(MALK\) jest równoległobokiem.
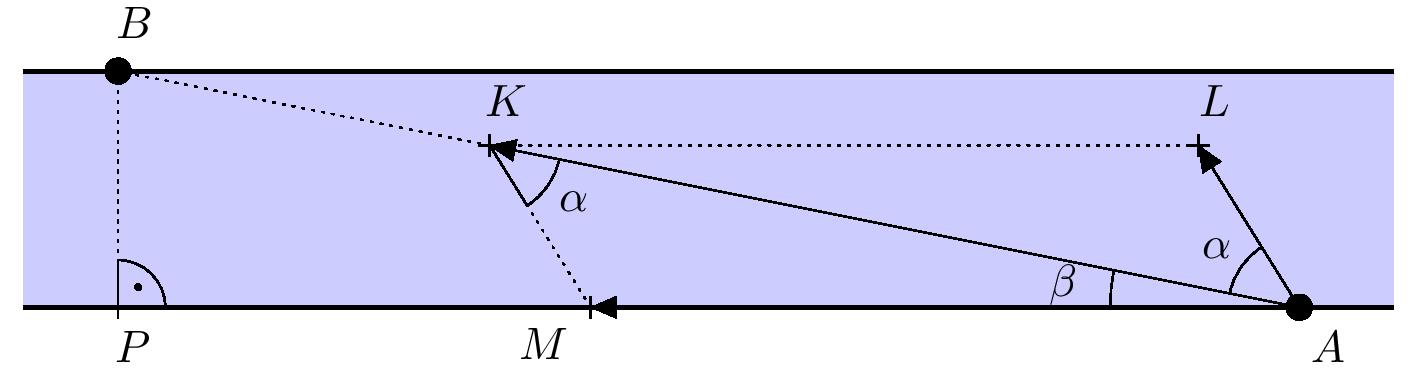
Dalej, oznaczmy \(\lvert \sphericalangle MAK \rvert = \beta\). Następnie \(\lvert \sphericalangle MAL \rvert = \alpha + \beta\). Z tego wynika, że \(|BP|=100\ \text{m}\) i \(|AP|=500\ \text{m}\). Korzystając z funkcji stycznej w trójkącie prostokątnym \(PAB\) otrzymujemy \(\beta = \arctan\frac{1}{5} \approx 11^{\circ}19'\).
Ponieważ równoległobok jest dzielony przez swoją przekątną na dwa przystające trójkąty, to \(\lvert \sphericalangle AKM \rvert= \lvert \sphericalangle KAL \rvert = \alpha\). Aby obliczyć \(\alpha\), wykorzystujemy prawo sinusów dla trójkąta \(AKM\). Po przekonwertowaniu długości boków na wspólną jednostkę (km w naszym rozwiązaniu), otrzymujemy konkretnie \(|KM|=12\text{km}\) i \(|AM|=2\cdot 3.6=7.2\text{km}\). Teraz wyrażamy \(\alpha\) z prawa sinusów:
\[ \begin{aligned} \frac{|KM|}{\sin \beta} &= \frac{|AM|}{\sin \alpha}\\[2mm] \sin \alpha &= \frac{|AM|}{|KM|}\cdot \sin\beta \qquad \Rightarrow \qquad \alpha = \arcsin \left( \frac{|AM|}{|KM|}\cdot \sin\beta \right) \end{aligned} \] Po podstawieniu wartości otrzymujemy \(\alpha \approx 6^{\circ}45'\). W związku z tym przewoźnik musi obrócić swoją łódź o około \(7^{\circ}\). w prawo od bezpośredniego kursu do miejsca docelowego.
Zadanie 2. Jeśli zegar cyfrowy na łodzi pokazuje 11:00 w momencie wypłynięcia (bez pokazywania sekund), jaką godzinę pokaże zegar w momencie przybycia łodzi do drugiego doku?
Rozwiązanie. Najpierw określmy odległość między dwoma dokami, korzystając z twierdzenia Pitagorasa w trójkącie prostokątnym \(ABP\):
\[ \begin{aligned} |AB| &= \sqrt{|AP|^2 + |BP|^2}\\ |AB| &= \sqrt{0.5^2 + 0.1^2}\\ |AB| &\approx 0.51\ \text{km}. \end{aligned} \]
Teraz określamy wielkość wypadkowej prędkości łodzi względem dna rzeki, która jest równa długości odcinka linii \(AK\). Można to wyznaczyć na przykład korzystając z prawa cosinusów w trójkącie \(AKM\). Oznaczamy kąt wewnętrzny \(\lvert \sphericalangle AMK \rvert =\gamma\), który mierzy \(180^{\circ}-\alpha - \beta \approx 161^{\circ}56'\). Następnie dla \(|AK|\) możemy napisać:
\[ \begin{aligned} |AK| &= \sqrt{|KM|^2 + |AM|^2 - 2\cdot |KM| \cdot |AM| \cdot \cos \gamma}\\ |AK| &= \sqrt{12^2 + 2^2 - 2\cdot 12 \cdot 2 \cdot \cos(161^{\circ}56')}\\ |AK| &\approx 19.0\ \text{km} \end{aligned} \] Łódź pokonuje bezpośrednią trasę o długości \(0,51\ \text{km}\) ze średnią prędkością \(19\ \text{km}/\text{h}\), co zajmuje: \[ \begin{aligned} t &= \frac{\text{pokonany dystans}}{\text{średnia prędkość}}\\ t &= \frac{0.51}{19}\ \text{h}\\ \end{aligned} \]
czyli około 97 sekund. Dlatego zegar pokaże 11:01 lub 11:02 po przybyciu do doku docelowego.