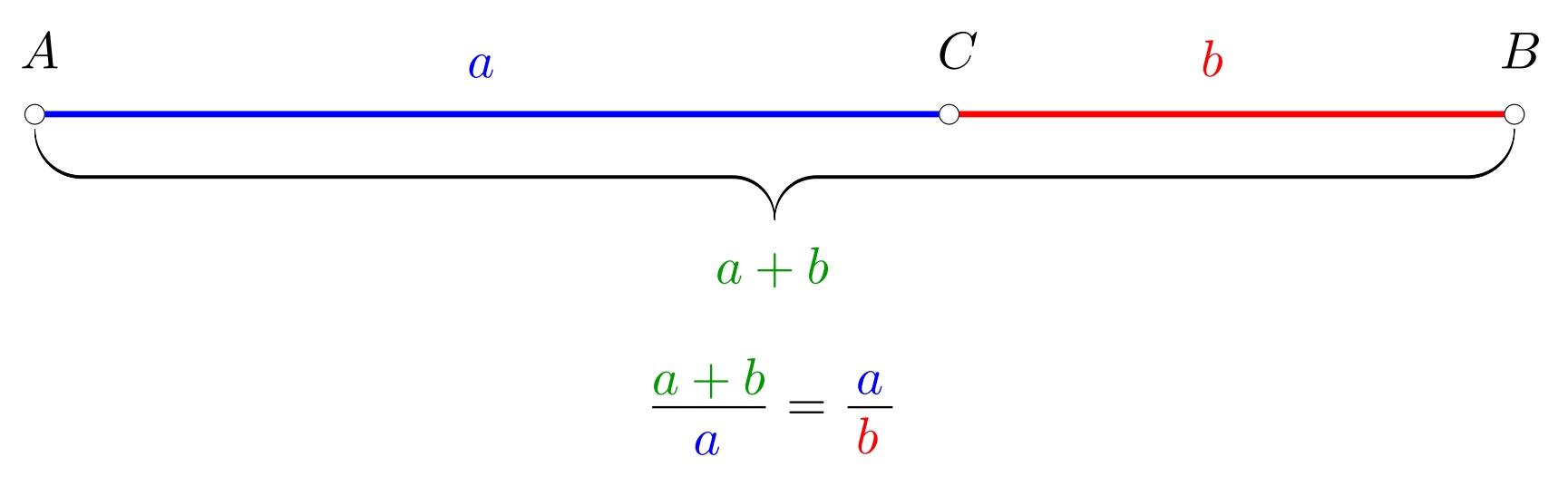
Mějme úsečku \(AB\) a na ní bod \(C\). Řekneme, že bod \(C\) dělí úsečku \(AB\) v poměru zlatého řezu, jestliže pro délky uvažovaných úseček platí vztah \[\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.\] Tento poměr se často značí řeckým písmenem \(\varphi\) a má hodnotu přibližně \(1{,}618\).
Pěkným příkladem využití zlatého řezu v běžném životě je platební karta. Ta má tvar tzv. zlatého obdélníka, jehož strany splňují poměr zlatého řezu. Zlatý obdélník je oblíbený tvar díky jeho vyváženému vzhledu; není ani příliš dlouhý, ani příliš široký.
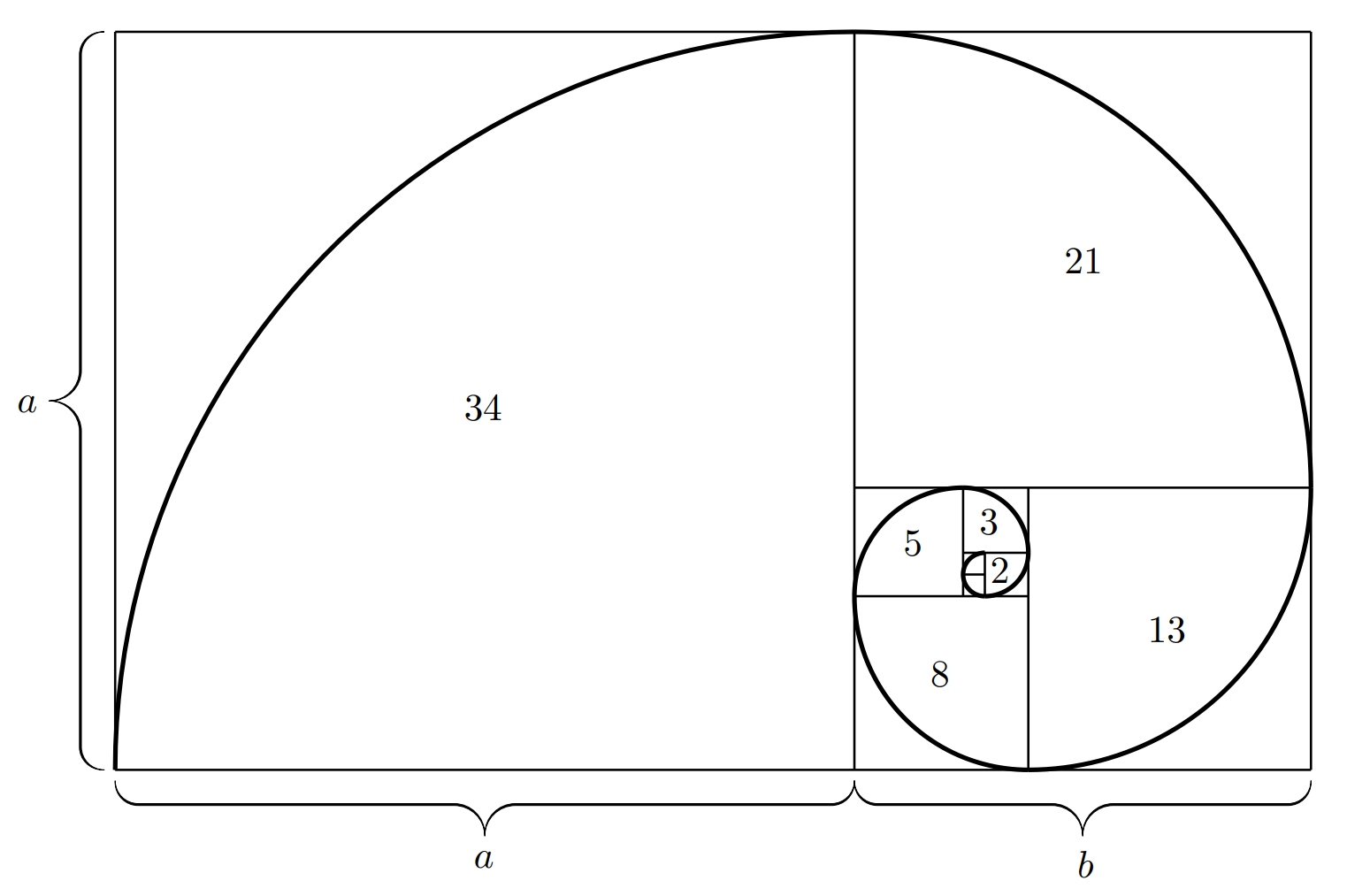
Zlatý řez úzce souvisí s Fibonacciho posloupností. Členy Fibonacciho posloupnosti jsou čísla \(1\), \(1\), \(2\), \(3\), \(5\), \(8\), \(13\), \(21\), \(34\), \(55\), …, kde každý další člen posloupnosti získáme součtem předchozích dvou členů. Jednotlivé prvky této posloupnosti označujeme také jako Fibonacciho čísla. A jaká je souvislost mezi Fibonacciho posloupností a zlatým řezem? Platí, že limita poměrů dvou po sobě jdoucích členů této posloupnosti je rovna právě zlatému řezu \(\varphi\).
Pokud sestrojíme čtverce, jejichž délky stran odpovídají právě Fibonacciho číslům, je možné je pěkně uspořádat vedle sebe do tvaru zlatého obdélníka tak, jak je vidět na obrázku. Do každého čtverce pak můžeme vepsat čtvrtkružnici a dostáváme tzv. zlatou spirálu. Zlatá spirála je speciálním případem logaritmické spirály.
V přírodě se zlatý řez objevuje právě ve formě Fibonacciho posloupnosti. Můžeme ho najít v uspořádání listů na stoncích. Listy vyrůstají nad sebou tak, aby si navzájem nestínily, přechod od jednoho listu k dalšímu má charakter šroubovitého výstupu kolem stonku. Podobné uspořádání můžeme najít u šupin borové šišky, semen slunečnice nebo u kůry ananasu. Logaritmickou spirálu najdeme také ve schránkách měkkýšů či ve svinutém lístku kapradiny. Tento tvar dále mají tornáda, cyklóny i galaxie.
Zlatý řez je hojně využíván v umění pro dosažení esteticky působivých a harmonických kompozic. Malíři a fotografové používají tento poměr k určení umístění klíčových prvků ve svých obrazech. Architekti často integrují poměr zlatého řez do návrhů budov.
Nekonečný řetězový zlomek je výraz typu \[x = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \ddots}}},\] kde \(a_0\) je celé číslo a čísla \(a_i\) jsou kladná přirozená čísla pro \(i\in\mathbb{N}\). Řetězový zlomek může být i v konečném tvaru.
Zlatý řez lze vyjádřit nekonečným řetězovým zlomkem \[\varphi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}.\]
Úloha 1. Vypočítejte přibližné hodnoty zlatého řezu pomocí následujících konečných řetězových zlomků
Řešení.
Úloha 2. Vypočtěte přesnou hodnotu zlatého poměru \(\varphi\).
Řešení. Předpokládejme, že úsečka \(AB\) má délku \(1\). Tuto úsečku rozdělíme bodem \(C\) v poměru zlatého řezu. Potom platí \[\varphi=\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.\] Označme \(x=|AC|\), tedy \(x\) bude délka delšího úseku úsečky \(AB\). Potom pro délku úsečky \(BC\) platí \(|BC|=1-x\) a tím získáme vztah \[\frac{1}{x} = \frac{x}{1-x},\tag{1}\] který má smysl pro \(x\neq0 \text{ a } x\neq1\). Tyto krajní hodnoty však nemusíme vyšetřovat, protože poměr zlatého řezu zcela jistě nesplňují. Úpravou (1) dostaneme kvadratickou rovnici \[x^2 + x - 1 = 0,\] jejíž kořeny jsou \[x_{1,2} = \frac{-1 \pm \sqrt{5}}{2}.\] V našem případě \(x\) je délka úsečky, proto záporná hodnota \(x\) nemá smysl. Máme tedy jediné vyhovující řešení rovnice (1) \[x_1 = \frac{-1 + \sqrt{5}}{2}.\] Nyní můžeme vypočítat hodnotu zlatého řezu \(\varphi\): \[\varphi=\frac{|AB|}{|AC|}=\frac{1}{x} = \frac{1}{\frac{-1 + \sqrt{5}}{2}}=\frac{2}{\sqrt{5}-1}.\] Usměrněním zlomku pak dostaneme \[\varphi=\frac{\sqrt{5}+1}{2}\doteq1{,}618.\]
Úloha 3. Řešte rovnici inspirovanou zlatým řezem v konečném řetězovém zlomku \[ x = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{x}}}. \]
Řešení.
Nejprve rovnici postupně zjednodušíme. \[ \begin{aligned} x &= 1 + \cfrac{1}{1 + \cfrac{1}{\frac{x+1}{x}}}\qquad\text{pro }x\neq0\\ x &= 1 + \cfrac{1}{1 + \cfrac{x}{x+1}}\qquad\text{pro }x\neq-1\\ x &= 1 + \cfrac{1}{\frac{x+1+x}{x+1}}\\ x &= 1 + \frac{x+1}{2x+1}\\ x &= \frac{3x+2}{2x+1}\\ \end{aligned} \]
Za podmínky \(x\neq -\frac12\) odsud úpravou získáme kvadratickou rovnici \[2x^2 - 2x - 2 = 0.\] Její kořeny jsou \[x_{1,2} = \frac{1 \pm \sqrt{5}}{2}.\] Všimněte si, že jedním z řešení je opět zlatý řez.