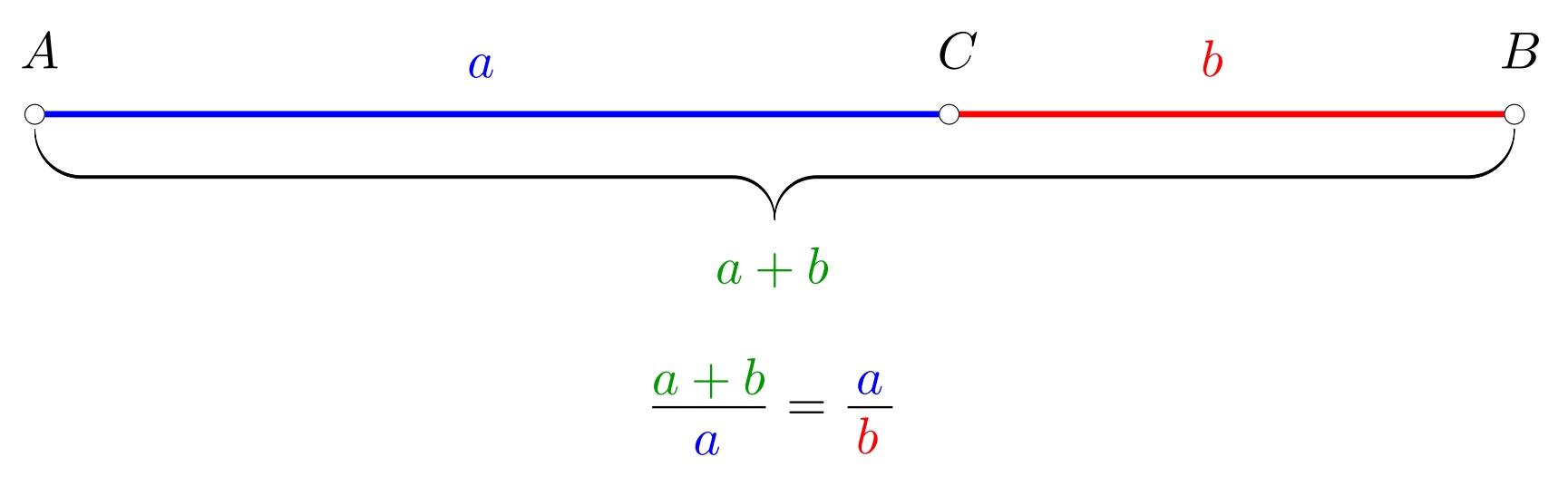
Sea un segmento de recta \(AB\) y un punto \(C\) que se encuentra sobre él. Decimos que el punto \(C\) divide el segmento \(AB\) en la proporción áurea, si las longitudes de los segmentos satisfacen la ecuación \[\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.\] Esta proporción se denota frecuentemente con la letra griega \(\varphi\) y tiene un valor aproximado de \(1{.}618\).
Un buen ejemplo del uso de la proporción áurea en la vida cotidiana es la tarjeta de crédito. Tiene la forma del llamado rectángulo áureo, cuyos lados satisfacen la proporción áurea. El rectángulo áureo es una forma popular por su aspecto equilibrado; no es ni demasiado largo ni demasiado ancho.
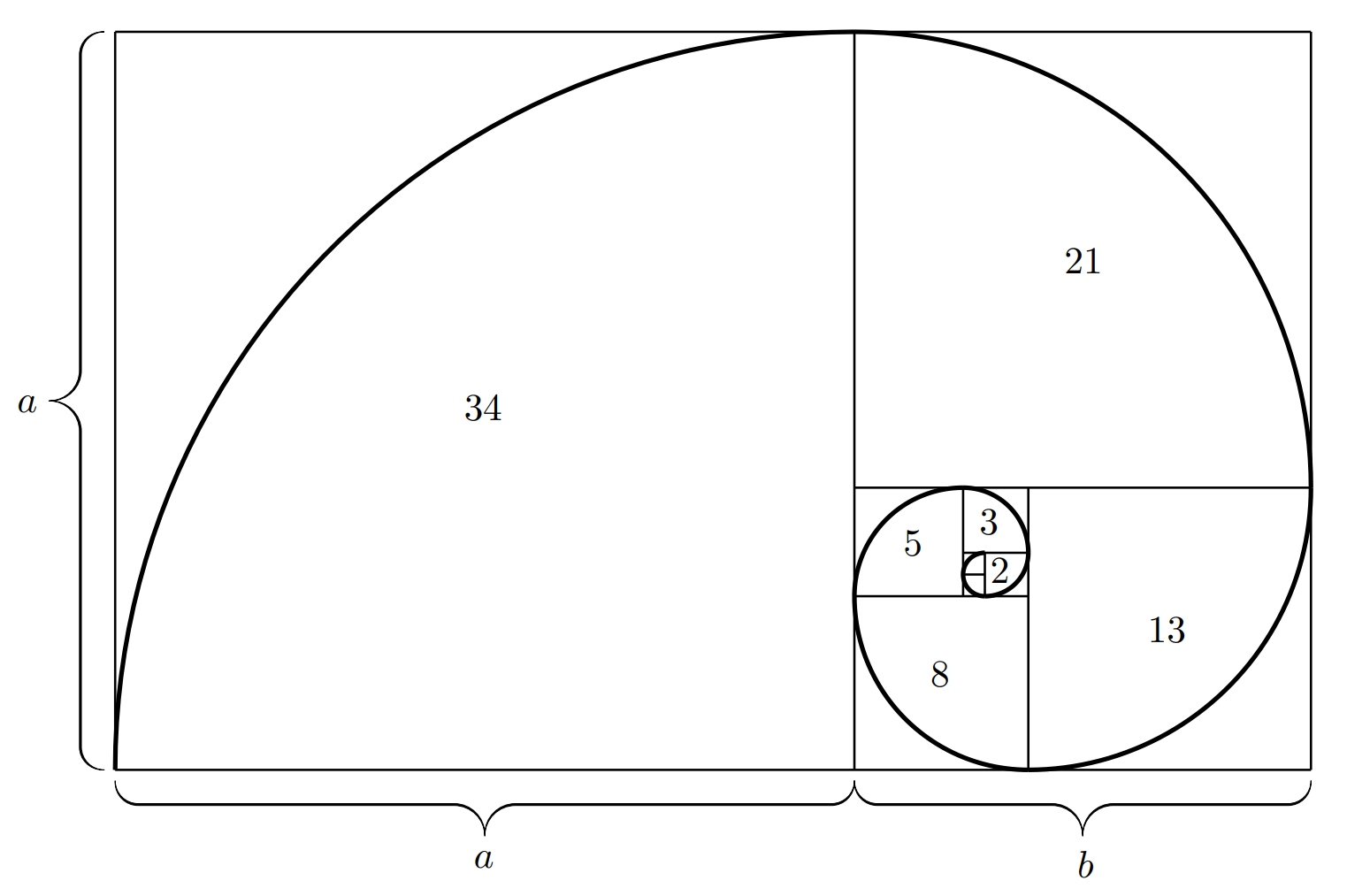
La proporción áurea está estrechamente relacionada con la sucesión de Fibonacci. Los términos de la sucesión de Fibonacci son números \(1\), \(1\), \(2\), \(3\), \(5\), \(8\), \(13\), \(21\), \(34\), \(55\), …, donde cada término es la suma de los dos anteriores. También nos referimos a los términos individuales de esta sucesión como números de Fibonacci. ¿Cuál es la relación entre la sucesión de Fibonacci y la proporción áurea? Se cumple que el límite del cociente entre dos términos consecutivos de esta sucesión es igual a la proporción áurea \(\varphi\).
Si construimos cuadrados cuyas longitudes laterales correspondan exactamente a los números de Fibonacci, es posible disponerlos bien uno junto a otro en forma de rectángulo áureo, como se muestra en la figura. A continuación, podemos inscribir un cuarto de círculo en cada cuadrado y obtenemos la llamada espiral áurea. La espiral áurea es un caso especial de la espiral logarítmica.
En la naturaleza, la proporción áurea aparece en forma de secuencia de Fibonacci. Podemos encontrarla en la disposición de las hojas en los tallos. Las hojas crecen una encima de otra para no hacerse sombra, la transición de una hoja a la siguiente tiene el carácter de un crecimiento en espiral alrededor del tallo. Se encuentran disposiciones similares en las escamas de la piña, las semillas del girasol o la cáscara de la piña. La espiral logarítmica también se encuentra en las conchas de los moluscos o en el helecho fiddlehead. Los tornados, los ciclones y las galaxias también tienen esta forma.
La proporción áurea se utiliza ampliamente en el arte para lograr composiciones estéticamente impactantes y armoniosas. Los pintores y fotógrafos utilizan esta proporción para determinar la ubicación de los elementos clave en sus obras. Los arquitectos suelen integrar la proporción áurea en el diseño de edificios.
Una fracción continua infinita es una expresión de la forma \[x = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \ddots}}},\] donde \(a_0\) es un número entero y los números \(a_i\) son números naturales positivos para \(i \in \mathbb{N}\). Una fracción continua también puede ser finita.
La proporción áurea puede expresarse mediante la fracción continua \[\varphi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}.\]
Ejercicio 1. Calcula valores aproximados de la proporción áurea mediante fracciones continuas finitas
Solución.
Ejercicio 2. Calcula el valor exacto de la proporción áurea \(\varphi\).
Solución. Supongamos que el segmento de recta \(AB\) tiene una longitud de \(1\). Dividimos este segmento por el punto \(C\) en la proporción áurea. Entonces tenemos: \[\varphi=\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.\] Denotemos \(x = |AC|\), es decir, \(x\) es la longitud del segmento más largo del segmento \(AB\). Entonces, para la longitud del segmento \(BC\) se cumple que \(|BC| = 1 - x\), y así obtenemos la ecuación: \[\frac{1}{x} = \frac{x}{1-x},\tag{1}\] la cual está definida para \(x \neq 0 \text{ y } x \neq 1\). Sin embargo, no necesitamos considerar estos valores extremos, ya que ciertamente no corresponden a la proporción áurea. Al manipular la ecuación (1), obtenemos una ecuación cuadrática.
\[x^2 + x - 1 = 0,\] cuyas raíces son \[x_{1,2} = \frac{-1 \pm \sqrt{5}}{2}.\] En nuestro caso, \(x\) es la longitud del segmento de recta; por lo tanto, un valor negativo de \(x\) no es válido. Así, tenemos la única solución satisfactoria de la ecuación (1) \[x_1 = \frac{-1 + \sqrt{5}}{2}.\] Ahora podemos calcular el valor de la sección áurea \(\varphi\): \[\varphi=\frac{|AB|}{|AC|}=\frac{1}{x} = \frac{1}{\frac{-1 + \sqrt{5}}{2}}=\frac{2}{\sqrt{5}-1}.\] Racionalizando el denominador obtenemos \[\varphi=\frac{\sqrt{5}+1}{2}\doteq1{.}618.\]
Ejercicio 3. Soluciona una ecuación inspirada en la proporción áurea en una fracción continua finita \[ x = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{x}}}. \]
Solución.
Simplifiquemos la ecuación paso a paso. \[ \begin{aligned} x &= 1 + \cfrac{1}{1 + \cfrac{1}{\frac{x+1}{x}}}\qquad\text{for }x\neq0\\ x &= 1 + \cfrac{1}{1 + \cfrac{x}{x+1}}\qquad\text{for }x\neq-1\\ x &= 1 + \cfrac{1}{\frac{x+1+x}{x+1}}\\ x &= 1 + \frac{x+1}{2x+1}\\ x &= \frac{3x+2}{2x+1}\\ \end{aligned} \]
Bajo la condición \(x \neq -\frac{1}{2}\) obtenemos una ecuación cuadrática. \[2x^2 - 2x - 2 = 0.\] Sus soluciones son \[x_{1,2} = \frac{1 \pm \sqrt{5}}{2}.\] Observa que una de las soluciones es, nuevamente, la proporción áurea.