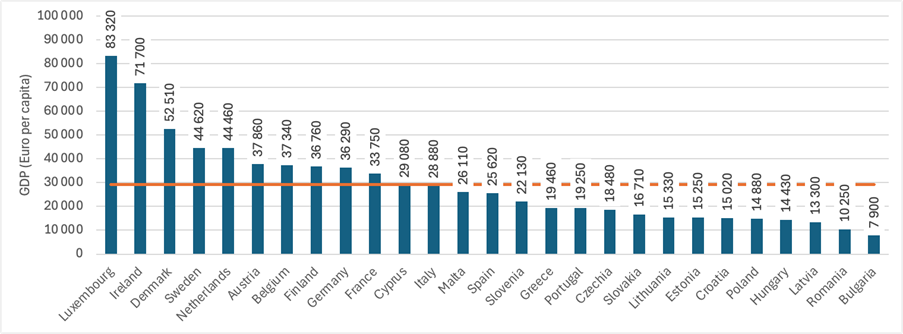
Hrubý domácí produkt (HDP, v angličtině GDP) je peněžním vyjádřením celkové hodnoty statků a služeb nově vytvořených v daném období na určitém území [1]. V makroekonomii se HDP používá jako ukazatel pro určování výkonnosti ekonomiky států. Můžeme jej tedy použít například pro srovnání výkonnosti jednotlivých států Evropské unie v roce 2023 (viz. Obr. 1).
Dalším využitím je sledování výkonnosti států v průběhu času. Podívejme se nyní například na to, jak se vyvíjelo HDP Evropské unie přepočtené na osobu v letech 2020 až 2023, kdy Evropská unie měla 27 členských států (viz Obr. 1). Časovou řadu (zdroj dat: [2]), která tento vývoj dokládá, vidíme na Obr. 2. (zdroj dat: Eurostat, https://ec.europa.eu/eurostat/databrowser/view/sdg_08_10/default/table, 17. 12. 2024)
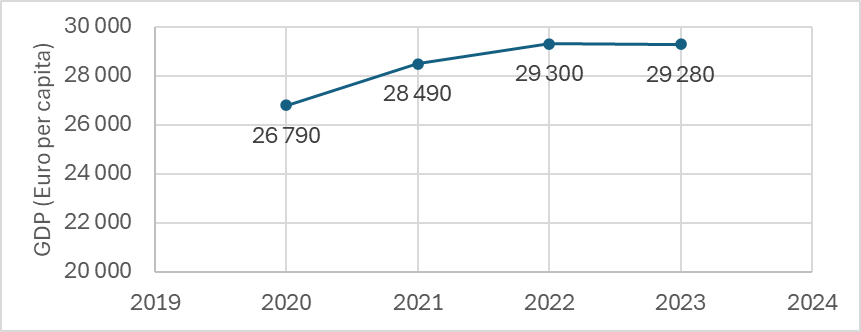
Časová řada, kterou vývoj HDP představuje, je tzv. intervalovou časovou řadou, tj. časovou řadou, jejíž údaje závisí na délce intervalu, který je sledován (v tomto případě na délce daného roku).
Nechť časovým okamžikům \(t_1,\,t_2,\,\ldots\,t_n\) odpovídají hodnoty časové řady \(y_1,\,y_2,\,\ldots\,y_n\).
Základní charakteristikou, kterou pro popis této časové řady používáme, je její průměr.
Průměr intervalové časové řady (\(\bar{y}\)) vypočteme jako prostý aritmetický průměr \[\bar{y} = \frac{y_1 + y_2 + \dots + y_n}{n}. \tag{1}\]
Kromě průměru nás mnohdy zajímají základní míry dynamiky časových řad, které umožňují charakterizovat základní rysy jejich “chování”.
Absolutní přírůstky (\(\Delta y_t\)) Nejjednodušší mírou dynamiky je absolutní přírůstek, který nám říká „o kolik“ se změnila časová řada mezi jednotlivými okamžiky. \[\Delta y_t = y_t - y_{t-1}, \quad t = 2,\,3, \,\dots,\, n.\tag{2}\]
Průměrný absolutní přírůstek (\(\bar{\Delta}\)) nám říká „o kolik“ se průměrně změnila časová řada za období mezi dvěma měřeními během sledovaného období.
Součet absolutních přírůstků vyjadřuje celkovou změnu časové řady za sledované období („o kolik“ se změnila časová řada mezi časy \(t_1\) a \(t_n\)): \[ \Delta y_2 + \Delta y_3 + \dots + \Delta y_n = (y_2 - y_1) + (y_3 - y_2) + \dots + (y_n - y_{n-1}) = y_n - y_1. \]
Průměrný absolutní přírůstek proto určíme jako aritmetický průměr absolutních přírůstků:
\[ \bar{\Delta} = \frac{\Delta y_2 + \Delta y_3 + \dots + \Delta y_n}{n-1} = \frac{y_n - y_1}{n-1}.\tag{3} \]
Všimněme si, že pro výpočet stačí znát počáteční hodnotu \(y_1\), koncovou hodnotu \(y_n\) a počet hodnot \(n\).
Koeficienty růstu (tempa růstu, \(k_t\)) Další mírou dynamiky časových řad jsou tzv. koeficienty růstu, nazývané taky tempa růstu. Koeficienty růstu udávají „kolikrát“ se změnila časová řada mezi jednotlivými časovými okamžiky
\[k_t = \frac{y_t}{y_{t-1}}, \quad t = 2,\,3,\, \dots,\, n.\tag{4}\]
Průměrný koeficient růstu (\(\bar{k}\)) nám říká „kolikrát“ se průměrně změnila časová řada mezi dvěma měřeními během sledovaného období.
V tomto případě je celkový koeficient růstu („kolikrát“ se změnila časová řada mezi časy \(t_1\) a \(t_n\)) nikoliv součtem, ale součinem dílčích koeficientů růstu \[ k_2 \cdot k_3 \cdot \ldots \cdot k_n = \frac{y_2}{y_1} \cdot \frac{y_3}{y_2} \cdot \ldots \cdot \frac{y_n}{y_{n-1}} = \frac{y_n}{y_1}. \] Průměrný koeficient růstu tedy určíme jako geometrický průměr dílčích koeficientů růstu \[\bar{k} =\sqrt[n-1]{k_2 \cdot k_3 \cdot \ldots \cdot k_n} =\sqrt[n-1]{\frac{y_n}{y_1}}.\tag{5}\]
Podobně jako při výpočtu průměrného absolutního přírůstku, i v tomto případě stačí pro výpočet znát počáteční hodnotu \(y_1\), koncovou hodnotu \(y_n\) a počet hodnot \(n\).
Relativní přírůstky (\(\delta_t\)): Chceme-li vědět „o kolik procent“ se změnila časová řada mezi jednotlivými okamžiky, použijeme relativní přírůstky, které snadno určíme pomocí koeficientů růstu:
\[ \delta_t = \frac{\Delta y_t}{y_{t-1}} \cdot 100 = \frac{y_t - y_{t-1}}{y_{t-1}} \cdot 100 = \left(\frac{y_t}{y_{t-1}} - 1\right) \cdot 100 = (k_t - 1) \cdot 100, \quad t = 2,\,3,\, \dots,\, n. \tag{6} \]
Stačí si uvědomit, že víme-li například, že cena výrobků vzrostla \(1{,}5\) krát, víme, že vzrostla o \(50\% \,(=(1{,}5-1)\cdot100\%)\).
Průměrný relativní přírůstek (\(\bar{\delta}\)) Udává, o kolik procent se průměrně změnila časová řada za období mezi dvěma měřeními během sledovaného období. Vypočteme jej pomocí průměrného koeficientu růstu: \[\bar{\delta} = (\bar{k} - 1) \times 100.\tag{7}\]
Poznámka Součet (součin) dílčích relativních přírůstků není roven celkovému relativnímu přírůstku („o kolik procent“ se změnila časová řada mezi časy \(t_1\) a \(t_n\)), proto pro výpočet průměrného relativního přírůstku nelze použít aritmetický ani geometrický průměr dílčích relativních přírůstků.
Nyní se pokusíme o základní popis časové řady prezentující vývoj HDP (v eurech na osobu), kterou najdeme na Obr. 2.
Úloha 1. Určete průměrné roční HDP (v eurech na osobu) Evropské unie v letech 2020 až 2023.
Řešení Jak bylo uvedeno ve vztahu (1), průměrné roční HDP určíme jako prostý aritmetický průměr analyzované časové řady
\[ \bar{y} = \frac{y_1 + y_2 + y_3 + y_4}{4} = \frac{26\,790 + 28\,490 + 29\,300 + 29\,280}{4} \approx 28\,465. \]
V letech 2023-2024 bylo průměrné roční HDP Evropské unie \(28\,465\) eur na osobu.
Úloha 2. Určete meziroční přírůstky HDP (v eurech na osobu) Evropské unie v letech 2020 až 2023 a odpovídající průměrný meziroční přírůstek HDP za toto období.
Řešení. Meziroční přírůstky HDP nám říkají „o kolik“ se meziročně změnilo HDP. Určíme je proto jako absolutní přírůstky dle vztahu (2), viz Tab. 1.
Tab 1: Základní míry dynamiky vývoje HDP v Evropské unii (přepočteno na osobu) v letech 2020 - 2023 (I)
| rok | HDP (Euro/osoba) | Meziroční přírůstky HDP (Euro/osoba) |
|---|---|---|
| 2020 | \(26\,790\) | — |
| 2021 | \(28\,490\) | \(28\,490 - 26\,790 = 1\,700\) |
| 2022 | \(29\,300\) | \(29\,300 - 28\,490 = 810\) |
| 2023 | \(29\,280\) | \(28\,280 - 29\,300 = -20\) |
| průměr | \(28\,465\) | \(830\) |
Průměrný meziroční přírůstek nyní můžeme dle vztahu (3) určit jako aritmetický průměr meziročních přírůstků nebo pouze pomocí počáteční a koncové hodnoty analyzované časové řady:
\[
\bar{\Delta} = \frac{\Delta y_2 + \Delta y_3 + \Delta y_4}{4-1} = \frac{1\,700 + 810 + (-20)}{3} = 830
\] nebo
\[
\bar{\Delta} = \frac{y_4 - y_1}{4-1} = \frac{29\,280 - 26\,790}{3} = 830.
\]
V letech 2020 až 2023 rostlo v Evropské unii HDP ročně v průměru o \(830\) Eur na osobu.
Průměrný přírůstek lze interpretovat rovněž tak, že pokud by se od roku 2020 (počáteční stav) HDP měnilo každý rok o 830 Eur na osobu (průměrný přírůstek), v roce 2023 by HDP odpovídalo uvedenému koncovému stavu.
Předpokládejme, že víme, že v letech 2020-2023 byl průměrný roční přírůstek HDP \(830\) Eur na osobu a v roce 2020 bylo HDP \(26\,790\) Eur na osobu. Vzhledem k tomu, že v daném období proběhly 3 meziroční změny, můžeme říci, že v roce 2023 bylo HDP
\[ 26\,790+3\cdot830=29\,280 \,\text{(Eur na osobu}). \]
Úloha 3. Určete meziroční tempa růstu HDP Evropské unie v letech 2020 až 2023 a odpovídající průměrné tempo růstu HDP za toto období.
Řešení. Meziroční tempa růstu HDP nám říkají „kolikrát“ se meziročně změnilo HDP. Určíme je proto jako koeficienty růstu dle vztahu (4), viz Tab. 2.
Tab. 2: Základní míry dynamiky vývoje HDP v Evropské unii (přepočteno na osobu) v letech 2020 - 2023 (II)
| rok | HDP (Euro/osoba) | Meziroční přírůstky HDP (Euro/osoba) | Tempo růstu (-) |
|---|---|---|---|
| 2020 | \(26\,790\) | — | — |
| 2021 | \(28\,490\) | \(1\,700\) | \(\frac{28\,490}{26\,790} \approx 1{,}063\) |
| 2022 | \(29\,300\) | \(810\) | \(\frac{29\,300}{28\,490} \approx 1{,}028\) |
| 2023 | \(29\,280\) | \(-20\) | \(\frac{29\,280}{29\,300} \approx 0{,}999\) |
| průměr | \(28\,465\) | \(830\) | — |
Průměrné meziroční tempo růstu nyní můžeme dle vztahu (5) určit jako geometrický průměr meziročních temp růstů nebo pouze pomocí počáteční a koncové hodnoty analyzované časové řady:
\[ \bar{k} = \sqrt[n-1]{k_2 \cdot k_3 \cdot k_4} = \sqrt[3]{1{,}063 \cdot 1{,}028 \cdot 0{,}999} \approx 1{,}030 \]
nebo
\[ \bar{k} = \sqrt[n-1]{\frac{y_4}{y_1}} = \sqrt[3]{\frac{29\,280}{26\,790}} \approx 1{,}030 \]
V letech 2020 až 2023 bylo v Evropské unii průměrné meziroční tempo růstu HDP (Eur na osobu) \(1{,}030\), tj. HDP (Eur na osobu) rostlo meziročně v průměru o \(3.0\%\).
Poznámka Budeme-li počítat průměrné tempo růstu jako geometrický průměr dílčích koeficientů růstu uvedených v Tab. 2, budeme pracovat se zaokrouhlenými údaji a vnášet tak do výpočtu chybu s tímto související. Proto doporučujeme pro výpočet používat raději pouze počáteční a koncové hodnoty analyzované časové řady.
Průměrné tempo růstu lze interpretovat rovněž tak, že pokud by se od roku 2020 (počáteční stav) HDP zvyšovalo každý rok \(1{,}030\) krát (průměrné tempo růstu), v roce 2023 by HDP odpovídalo uvedenému koncovému stavu.
Předpokládejme, že víme, že v letech 2020-2023 bylo průměrné tempo růstu HDP cca \(1{,}030\) a v roce 2020 bylo HDP \(26\,790\) Eur na osobu. Vzhledem k tomu, že v daném období proběhly 3 meziroční změny, můžeme říci, že v roce 2023 bylo HDP cca
\[ 26\,790\cdot 1{,}030^3≈29\,274 \, \text{(Eur na osobu)}. \]
Protože jsme v našem výpočtu použili zaokrouhlenou hodnotu průměrného tempa růstu, dopustili jsme se chyby. Vzhledem k tomu, že skutečnou hodnotu HDP v roce 2023 známe (a příklad jsme řešili pouze jako ilustrační), můžeme určit velikost chyby, které jsme se dopustili. V tomto případě jsme skutečnou hodnotu HDP v roce 2023 (\(29\,280\) Eur na osobu) podhodnotili o \(6\) Eur na osobu, tj. o \(0{,}02\%\).
Úloha 4. Určete meziroční relativní přírůstky HDP Evropské unie v letech 2020 až 2023 a odpovídající průměrný relativní přírůstek HDP za toto období.
Řešení Tento úkol jsme již vyřešili v rámci interpretace temp růstů zjištěných v úloze 3. Říkáme-li, že v roce 2021 vzrostlo HDP meziročně \(1{,}063\) krát, je to totéž jako když budeme tvrdit, že v roce 2021 vzrostlo HDP meziročně o \(6.3\%\).
To tvrdí i vztahy (6) a (7), které uvádějí, jak souvisí relativní přírůstek v procentech (resp. průměrný relativní přírůstek v procentech) a tempo růstu (resp. průměrné tempo růstu).
Výsledky jsou uvedeny v Tab. 3.
Tab. 3: Základní míry dynamiky vývoje HDP v Evropské unii (přepočteno na osobu) v letech 2020 - 2023 (III)
| rok | HDP (Euro/osoba) | Meziroční přírůstky HDP (Euro/osoba) | Tempo růstu (-) | Relativní přírůstek (%) |
|---|---|---|---|---|
| 2020 | \(26\,790\) | — | — | — |
| 2021 | \(28\,490\) | \(1\,700\) | \(1{,}063\) | \(6{,}3\) |
| 2022 | \(29\,300\) | \(810\) | \(1{,}028\) | \(2{,}8\) |
| 2023 | \(29\,280\) | \(-20\) | \(0{,}999\) | \(-0{,}1\) |
| průměr | \(28\,465\) | \(830\) | \(1{,}030\) | \(3{,}0\) |