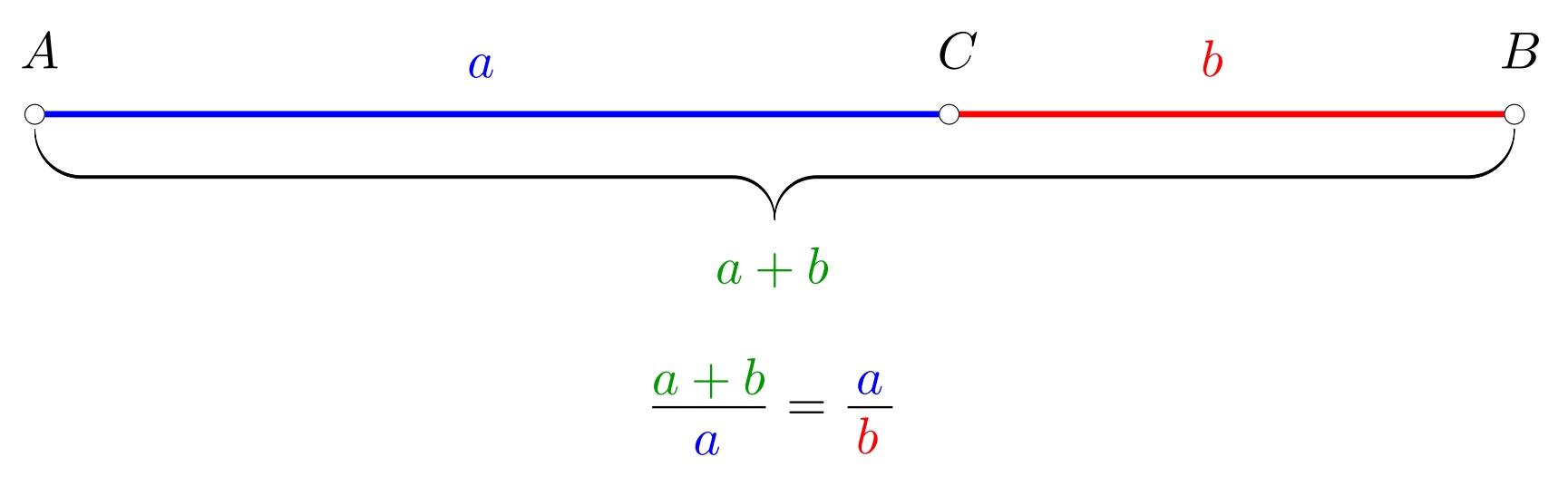
Mamy odcinek \(AB\) i punkt \(C\), który na nim leży. Mówimy, że punkt \(C\) dzieli odcinek \(AB\) w złotym podziale, jeśli długości odcinków spełniają równanie \[\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.\] Współczynnik ten jest często oznaczany grecką literą \(\varphi\) i ma wartość około \(1{.}618\).
Dobrym przykładem zastosowania złotego podziału w życiu codziennym jest karta kredytowa. Ma ona kształt tak zwanego złotego prostokąta, którego boki spełniają zasadę złotego podziału. Złoty prostokąt jest popularnym kształtem ze względu na jego zrównoważony wygląd; nie jest ani za długi, ani za szeroki.
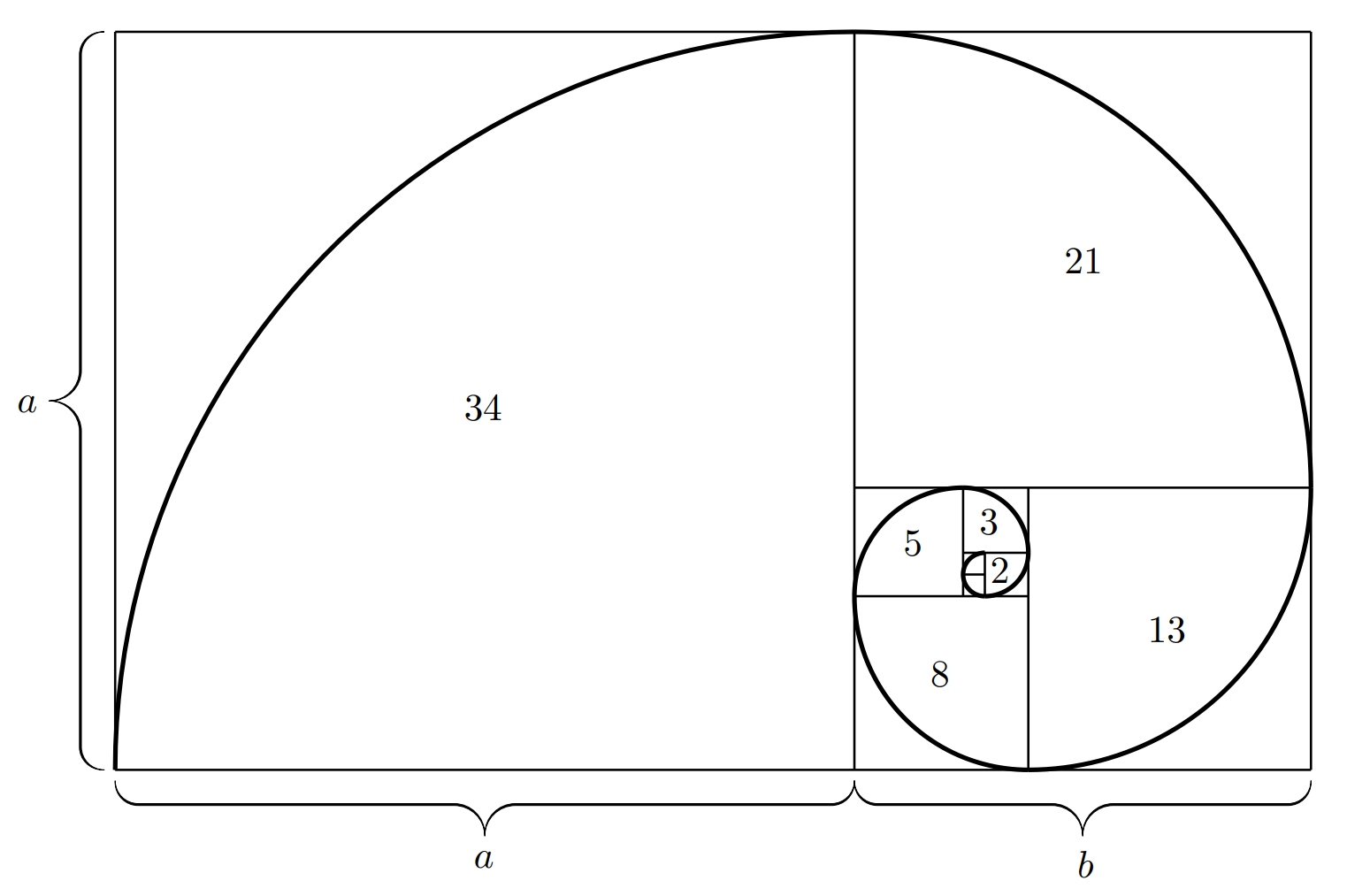
Złota proporcja jest ściśle związana z ciągiem Fibonacciego. Wyrazy ciągu Fibonacciego są liczbami \(1\), \(1\), \(2\), \(3\), \(5\), \(8\), \(13\), \(21\), \(34\), \(55\), …,gdzie każdy termin jest sumą dwóch poprzednich. Poszczególne wyrazy tego ciągu nazywamy również liczbami Fibonacciego. Jaki jest związek między ciągiem Fibonacciego a złotą proporcją? Jest tak, że granica stosunku dwóch kolejnych wyrazów tego ciągu tego ciągu jest równa złotej proporcji \(\varphi\).
Jeśli skonstruujemy kwadraty, których długości boków odpowiadają dokładnie liczbom Fibonacciego, można je ładnie ułożyć obok siebie w kształcie złotego prostokąta, jak pokazano na rysunku. Następnie możemy wpisać ćwierć koła w każdy kwadrat i otrzymamy tzw. złotą spiralę. Złota spirala jest szczególnym przypadkiem spirali logarytmicznej.
W naturze złota proporcja występuje w postaci ciągu Fibonacciego. Możemy ją znaleźć w układzie liści na łodygach. Liście rosną jeden nad drugim, dzięki czemu nie zacieniają się nawzajem, przejście od jednego liścia do następnego ma charakter spiralnego wzrostu wokół łodygi. Podobny układ występuje w łuskach szyszek sosnowych, nasionach słonecznika lub skórce ananasa. Spirala logarytmiczna występuje również w muszlach mięczaków lub w paproci. Tornada, cyklony i galaktyki również mają ten kształt.
Złota proporcja jest szeroko stosowana w sztuce w celu uzyskania estetycznych i harmonijnych kompozycji. i harmonijnych kompozycji. Malarze i fotografowie używają tego współczynnika do określania rozmieszczenia kluczowych elementów w swoich pracach. Architekci często uwzględniają złotą proporcję w projektach budynków.
Nieskończony ułamek ciągły jest wyrażeniem postaci \[x = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \ddots}}},\] gdzie \(a_0\) jest liczbą całkowitą, a liczby \(a_i\) są dodatnimi liczbami naturalnymi dla \(i\in\mathbb{N}\). Ułamek ciągły może być również skończony.
Złotą proporcję można wyrazić za pomocą ułamka ciągłego \[\varphi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}.\]
Zadanie 1. Oblicz przybliżone wartości złotej proporcji przy użyciu skończonych ułamków ciągłych
Rozwiązanie.
Zadanie 2. Oblicz dokładną wartość złotego podziału \(\varphi\).
Rozwiązanie. Załóżmy, że odcinek \(AB\) ma długość \(1\). Podzielimy ten odcinek przez punkt \(C\) w złotym podziale. Wtedy otrzymujemy \[\varphi=\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.\] Oznaczmy \(x=|AC|\), tzn. \(x\) jest długością dłuższego odcinka linii \(AB\). Wtedy \(|BC|=1-x\) zachodzi dla długości odcinka \(BC\) i w ten sposób otrzymujemy równanie \[\frac{1}{x} = \frac{x}{1-x},\tag{1}\]. który jest zdefiniowany dla \(x\neq0 \text{ i } x\neq1\). Nie musimy jednak brać pod uwagę tych skrajnych wartości, ponieważ z pewnością nie odpowiadają one złotej proporcji. Manipulując (1), otrzymujemy równanie kwadratowe \[x^2 + x - 1 = 0,\]. którego pierwiastkami są \[x_{1,2} = \frac{-1 \pm \sqrt{5}}{2}.\] W naszym przypadku, \(x\) jest długością odcinka linii; dlatego ujemna wartość \(x\) nie jest prawidłowa. Mamy więc jedyne satysfakcjonujące rozwiązanie równania (1) \[x_1 = \frac{-1 + \sqrt{5}}{2}.\] Teraz możemy obliczyć wartość złotego podziału \(\varphi\): \[\varphi=\frac{|AB|}{|AC|}=\frac{1}{x} = \frac{1}{\frac{-1 + \sqrt{5}}{2}}=\frac{2}{\sqrt{5}-1}.\] Skracając mianownik otrzymujemy wówczas \[\varphi=\frac{\sqrt{5}+1}{2}\doteq1{.}618.\]
Zadanie 3. Rozwiąż równanie inspirując się złotą proporcją w skończonym ułamku ciągłym \[ x = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{x}}}. \]
Rozwiązanie.
Uprośćmy równanie krok po kroku. \[ \begin{aligned} x &= 1 + \cfrac{1}{1 + \cfrac{1}{\frac{x+1}{x}}}\qquad\text{for }x\neq0\\ x &= 1 + \cfrac{1}{1 + \cfrac{x}{x+1}}\qquad\text{for }x\neq-1\\ x &= 1 + \cfrac{1}{\frac{x+1+x}{x+1}}\\ x &= 1 + \frac{x+1}{2x+1}\\ x &= \frac{3x+2}{2x+1}\\ \end{aligned} \]
Pod warunkiem \(x\neq -\frac12\) otrzymujemy równanie kwadratowe \[2x^2 - 2x - 2 = 0.\] Jego pierwiastki to \[x_{1,2} = \frac{1 \pm \sqrt{5}}{2}.\] Zauważ, że jednym z rozwiązań jest ponownie złota proporcja.