Zlatý rez a reťazový zlomok

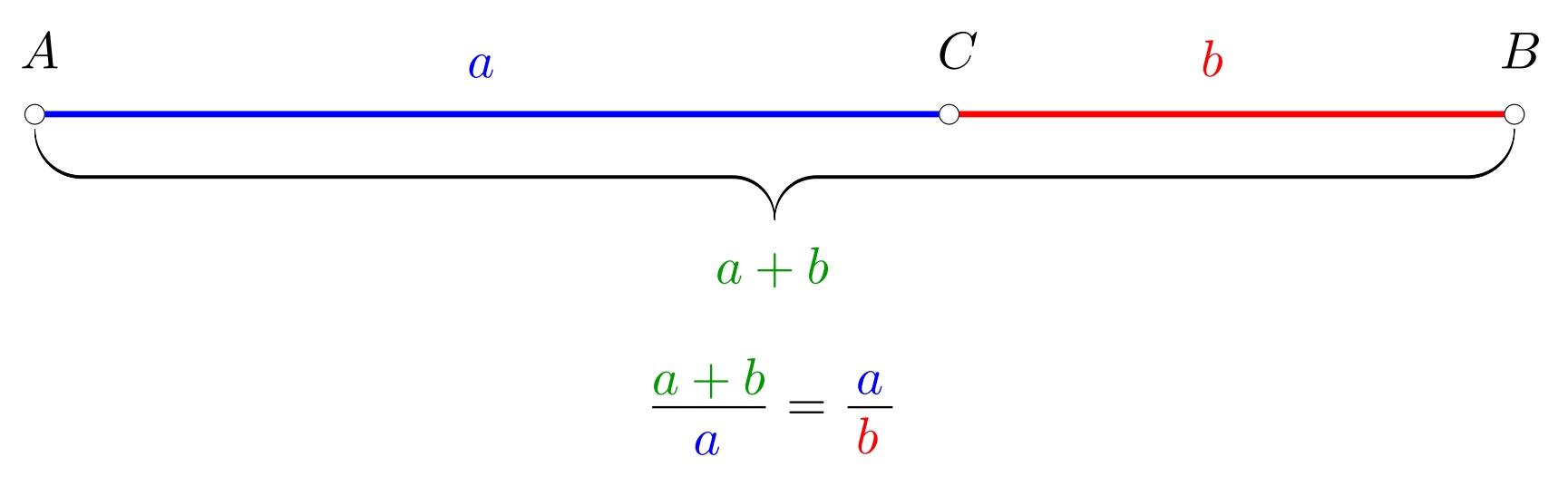
40 min., 1/3

Majme úsečku \(AB\) a bod \(C\), ktorý na nej leží. Bod \(C\) rozdeľuje úsečku \(AB\) v zlatom reze, ak dĺžky úsekov spĺňajú rovnicu \[\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.\] Tento pomer sa často označuje gréckym písmenom \(\varphi\) a má hodnotu približne \(1{,}618\).

Zlatý rez sa v bežnom živote využíva napríklad pri platobných kartách. Tie majú tvar tzv. zlatého obdĺžnika, ktorého strany spĺňajú pomer zlatého rezu. Zlatý obdĺžnik je obľúbený pre svoj vyvážený vzhľad – nie je ani príliš dlhý, ani príliš široký.

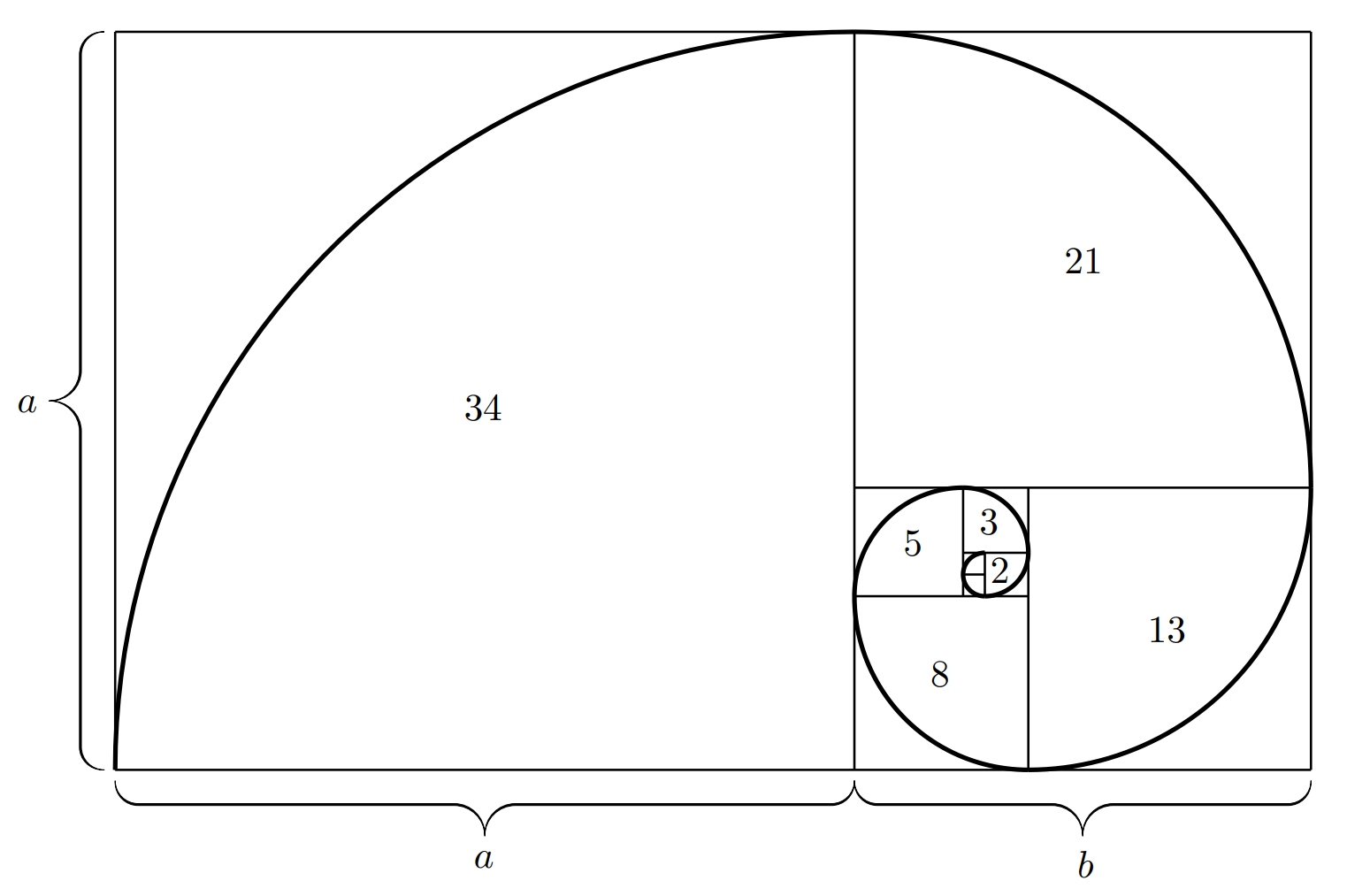
Zlatý rez úzko súvisí s Fibonacciho postupnosťou. Členy tejto postupnosti sú čísla \(1\), \(1\), \(2\), \(3\), \(5\), \(8\), \(13\), \(21\), \(34\), \(55\), …, kde každý ďalší člen postupnosti získame súčtom dvoch predchádzajúcich členov. Jednotlivé členy tejto postupnosti nazývame Fibonacciho čísla. Aká je súvislosť medzi Fibonacciho postupnosťou a zlatým rezom? Platí, že limita podielu dvoch po sebe idúcich členov tejto postupnosti sa rovná zlatému rezu \(\varphi\). Ak zostrojíme štvorce, ktorých strany majú dĺžky zodpovedajúce práve Fibonacciho číslam, môžeme ich pekne usporiadať vedľa seba do tvaru zlatého obdĺžnika ako môžme vidieť na obrázku. Do každého štvorca môžeme vpísať štvrtinu kružnice a získame tzv. zlatú špirálu. Zlatá špirála je špeciálnym prípadom logaritmickej špirály.

V prírode sa zlatý rez objavuje vo forme Fibonacciho postupnosti. Nájdeme ho v usporiadaní listov na stonke – listy rastú jeden nad druhým tak, aby sa navzájom netienili, pričom prechod z jedného listu na druhý má charakter špirálovitého rastu okolo stonky. Podobné usporiadanie nájdeme v šupinách šišky, semenách slnečnice alebo v kôre ananásu. Logaritmická špirála sa vyskytuje aj v ulitách mäkkýšov či v mladých listoch papradí. Tento tvar tiež majú tornáda, cyklóny a galaxie.

Zlatý rez sa často využíva v umení na dosiahnutie esteticky pôsobiacich a harmonických kompozíciach. Maliari a fotografi používajú tento pomer na určenie umiestnenia kľúčových prvkov vo svojich dielach. Architekti často integrujú zlatý rez do návrhov budov.

Nekonečný reťazový zlomok

Nekonečný reťazový zlomok je výraz typu \[x = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \ddots}}},\] kde \(a_0\) je celé číslo a čísla \(a_i\) sú kladné prirozené čísla pre \(i\in\mathbb{N}\). Reťazový zlomok môže byť aj konečný.

Zlatý rez môžeme vyjadriť nekonečným reťazovým zlomkom \[\varphi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}.\]

Riešenie.

1. \[1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}= 1 + \cfrac{1}{1 + \cfrac{1}{2}}= 1 + \cfrac{1}{\frac{3}{2}}=\frac{5}{3}\doteq1{,}67\]
2. \[1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1}}}}=1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{2}}}=1 + \cfrac{1}{1 + \cfrac{1}{\frac{3}{2}}}=1 + \cfrac{1}{\frac{5}{3}}=\frac{8}{5}=1{,}6\]

Riešenie. Predpokladajme, že úsečka \(AB\) má dĺžku \(1\). Túto úsečku rozdelíme bodom \(C\) v zlatom reze. Potom platí \[\varphi=\frac{|AB|}{|AC|}=\frac{|AC|}{|CB|}.\] Označme \(x = |AC|\), teda \(x\) je dĺžka dlhšieho úseku úsečky \(AB\). Potom \(|BC| = 1 - x\) a dostávame rovnicu \[\frac{1}{x} = \frac{x}{1-x},\tag{1}\] ktorá je definovaná pre \(x\neq0 \text{ a } x\neq1\). Tieto krajné hodnoty nemusíme vyšetrovať, pretože určite pomer zlatého rezu nespĺňajú. Úpravou (1) dostaneme kvadratickú rovnicu \[x^2 + x - 1 = 0,\] ktorej korene sú \[x_{1,2} = \frac{-1 \pm \sqrt{5}}{2}.\] Keďže \(x\) je dĺžka úseku, záporná hodnota neprichádza do úvahy. Jediné vyhovujúce riešenie rovnice (1) je \[x_1 = \frac{-1 + \sqrt{5}}{2}.\] Teraz môžeme vypočítať hodnotu zlatého rezu \(\varphi\): \[\varphi=\frac{|AB|}{|AC|}=\frac{1}{x} = \frac{1}{\frac{-1 + \sqrt{5}}{2}}=\frac{2}{\sqrt{5}-1}.\] Usmernením zlomku potom dostaneme \[\varphi=\frac{\sqrt{5}+1}{2}\doteq1{,}618.\]

Riešenie. Zjednodusíme rovnicu krok za krokom. \[ \begin{aligned} x &= 1 + \cfrac{1}{1 + \cfrac{1}{\frac{x+1}{x}}}\qquad\text{pre }x\neq0\\ x &= 1 + \cfrac{1}{1 + \cfrac{x}{x+1}}\qquad\text{pre }x\neq-1\\ x &= 1 + \cfrac{1}{\frac{x+1+x}{x+1}}\\ x &= 1 + \frac{x+1}{2x+1}\\ x &= \frac{3x+2}{2x+1}\\ \end{aligned} \]

Za podmienky \(x\neq -\frac12\) dostaneme kvadratickú rovnicu \[2x^2 - 2x - 2 = 0.\] Jej korene sú \[x_{1,2} = \frac{1 \pm \sqrt{5}}{2}.\] Všimnime si, že jedno z riešení je opäť zlatý rez.

Literatúra

• Wikipedia. Golden ratio [online]. Dostupné z https://en.wikipedia.org/wiki/Golden_ratio [cit. 10.,11.,2023].
• Wikipedia. Řetězový zlomek [online]. Dostupné z https://cs.wikipedia.org/wiki/Řetězový_zlomek [cit. 10.,11.,2023].