Which of the routes between Lisbon and Washington shown on the map is shorter?
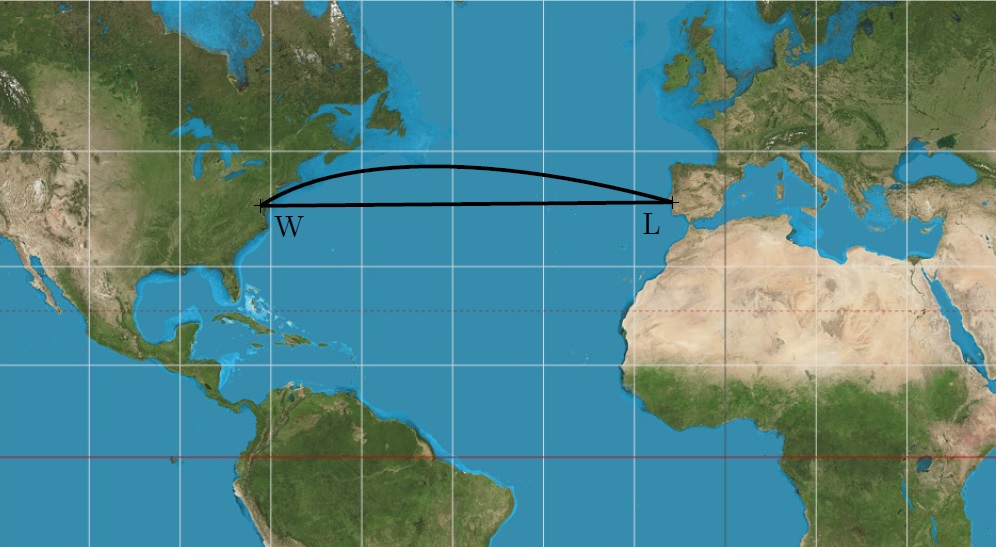
This seemingly simple question has a surprising answer, as you will see in this exercise. The shorter route is the arc, the longer one is the line segment. The reason is the distortion of the distances in the selected representation of the Earth’s surface. We see that the line segment \(LW\) on the map is approximately parallel to the geographic parallels on the Earth, so it actually corresponds to an arc on a circle that closely resembles a parallel (see the circle \(k\) with the center \(O\) in the figure).
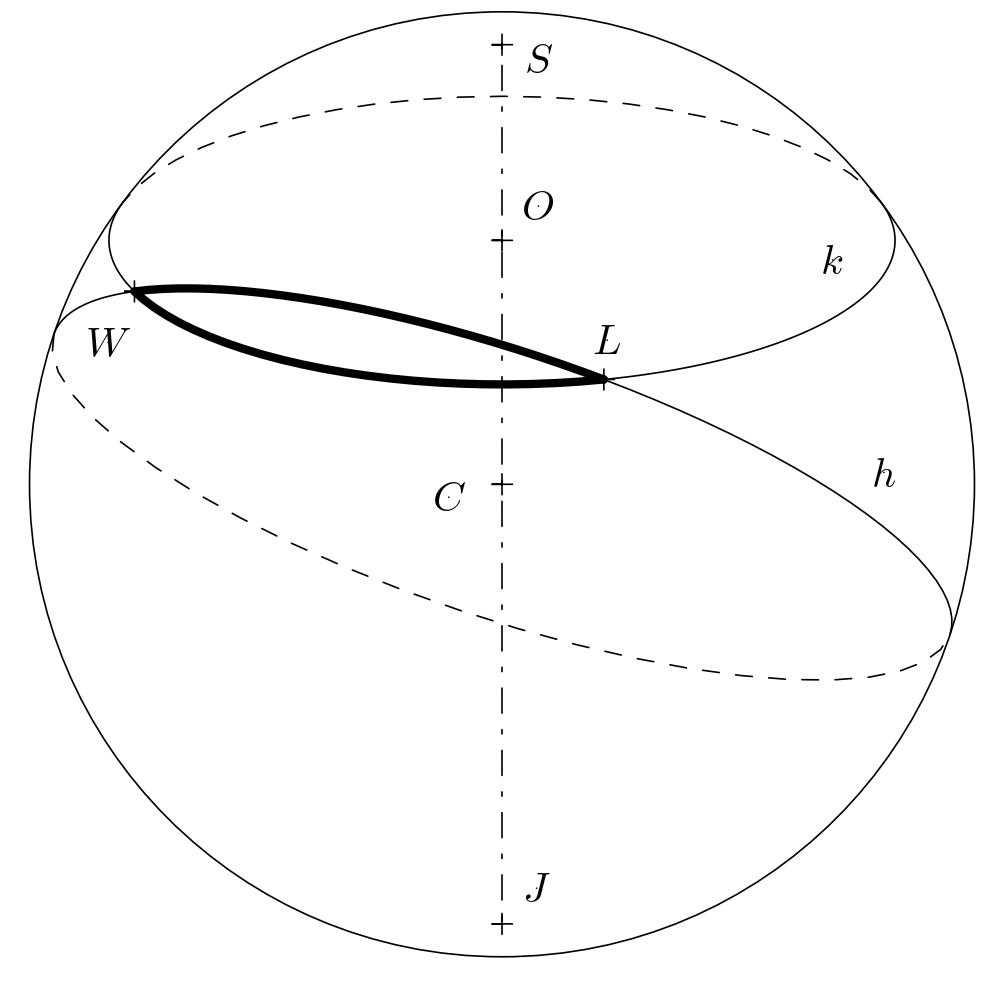
However, on the spherical surface (which we will consider to be the Earth’s surface in this task), the shortest distance is another arc. This arc is a part of a circle \(h\) whose center \(C\) is the center of the Earth. We refer to such paths as orthodromes and call all circles with this property great circles. How many kilometers do we save by traveling along an orthodrome? The answer to this question has to be calculated.
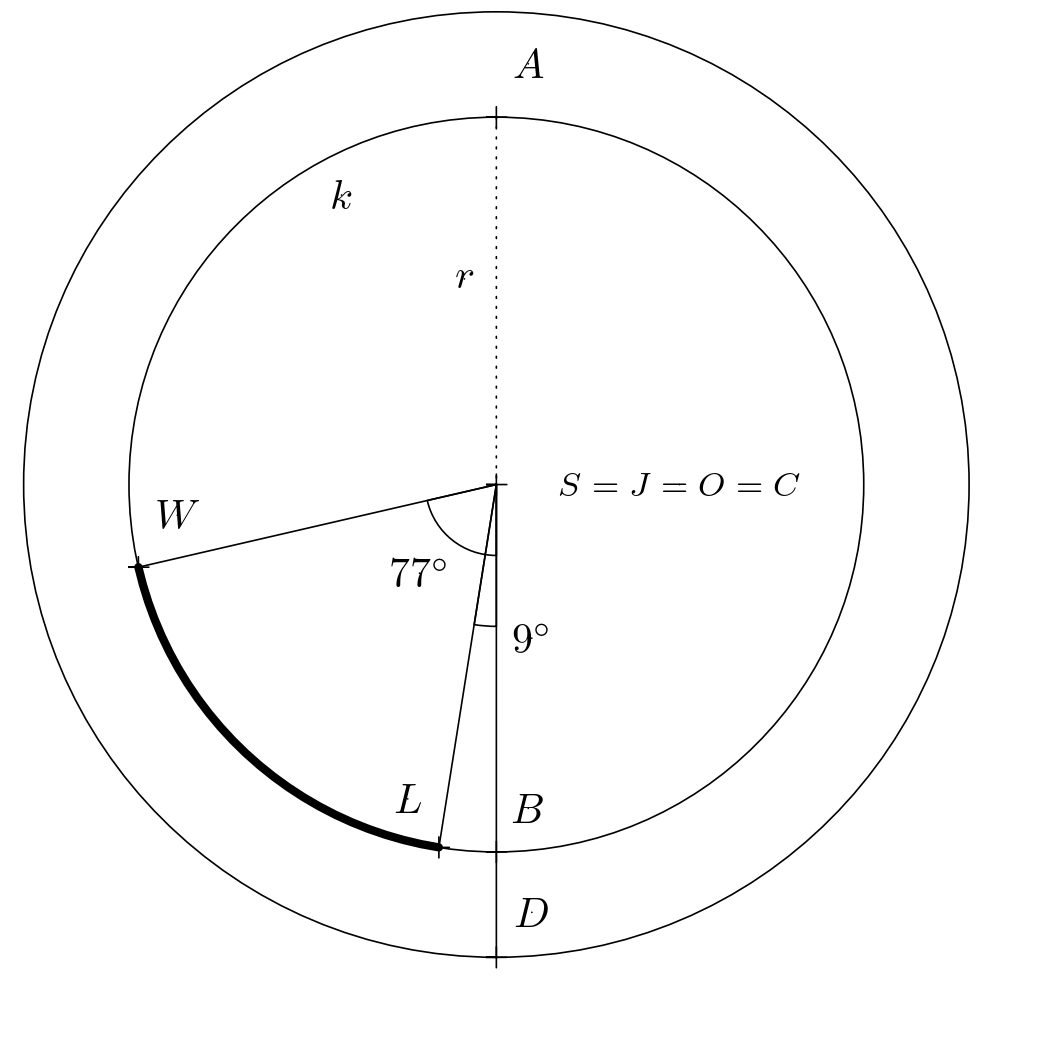
Exercise. Lisbon and Washington are located at approximately the same parallel (about \(39^{\circ}\) north latitude). How many kilometers does an airplane save by traveling on an orthodromic path compared to traveling on a parallel path? Lisbon is located at approximately \(9^{\circ}\) west longitude. Washington is located at \(77^{\circ}\) west longitude. Let us assume that the Earth is a sphere with center \(C\) and radius \(6,371\,\text{km}\) and that the plane flies at an average altitude of \(10\,\text{km}\) (take-off and landing are not taken into account). Therefore, in all considerations, we will work with a sphere of radius \(\varrho=6,381\,\text{km}\).
Solution. First, let’s determine how many kilometers the plane will cover while traveling along the parallel. Let us denote the parallel at \(39^{\circ}\) north latitude as a circle \(k\) with center \(O\) and radius \(r\). In an appropriate orthogonal projection of the globe (see the figure, where \(S\) and \(J\) are the poles), this circle appears as a chord \(AB\) with center \(O\).
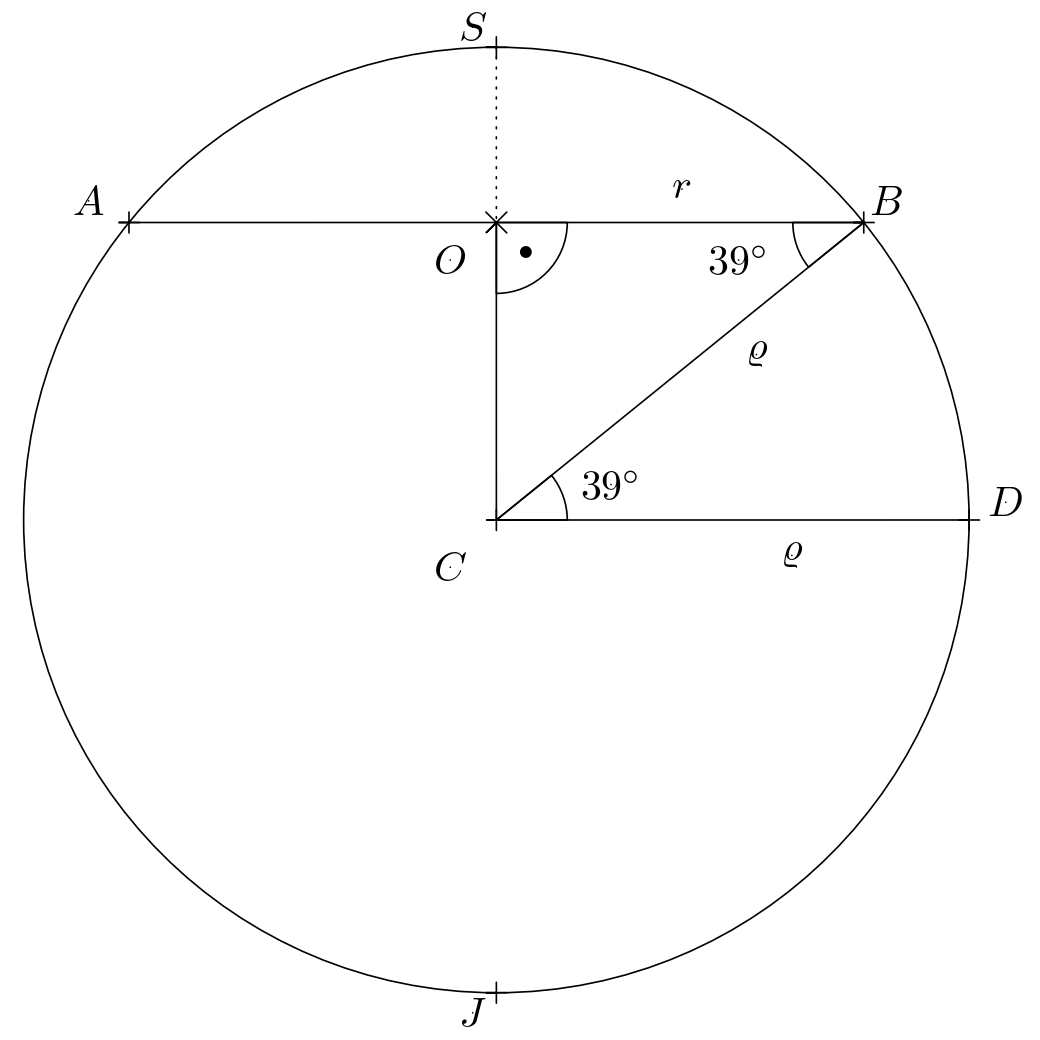
The figure shows the equality \(\lvert\sphericalangle CBO\rvert = \lvert\sphericalangle BCD\rvert\) (the angles are alternating) and by using the cosine function in the right-angled triangle \(BSO\) we get \(r=\varrho\cdot \cos 39^{\circ}\).
The trajectory of the plane moving along the parallel (in the figure below, the plane’s trajectory is represented by the shorter arc \(LW\)) is determined using direct proportion: the whole circle \(k\) has a length of \(2\pi r =2\pi\varrho\cdot\cos 39^{\circ} \,\text{km}\), i.e. the length of the shorter arc \(LW\) is equal to \[ \frac{(77-9)}{360}\cdot 2\pi\varrho\cdot \cos 39^{\circ} \doteq 5,885{.}4\,\text{km}. \]
Now, we determine how many kilometers the airplane covers while moving along the orthodrome. This is essentially the distance between two points on an imaginary sphere with the radius of \(\varrho=6,381\,\text{km}\). The figure shows that the orthodrome between points \(L\) and \(W\) is an arc of a certain great circle \(h\) with an unknown central angle \(\varphi\). We need to determine the measure of this angle.
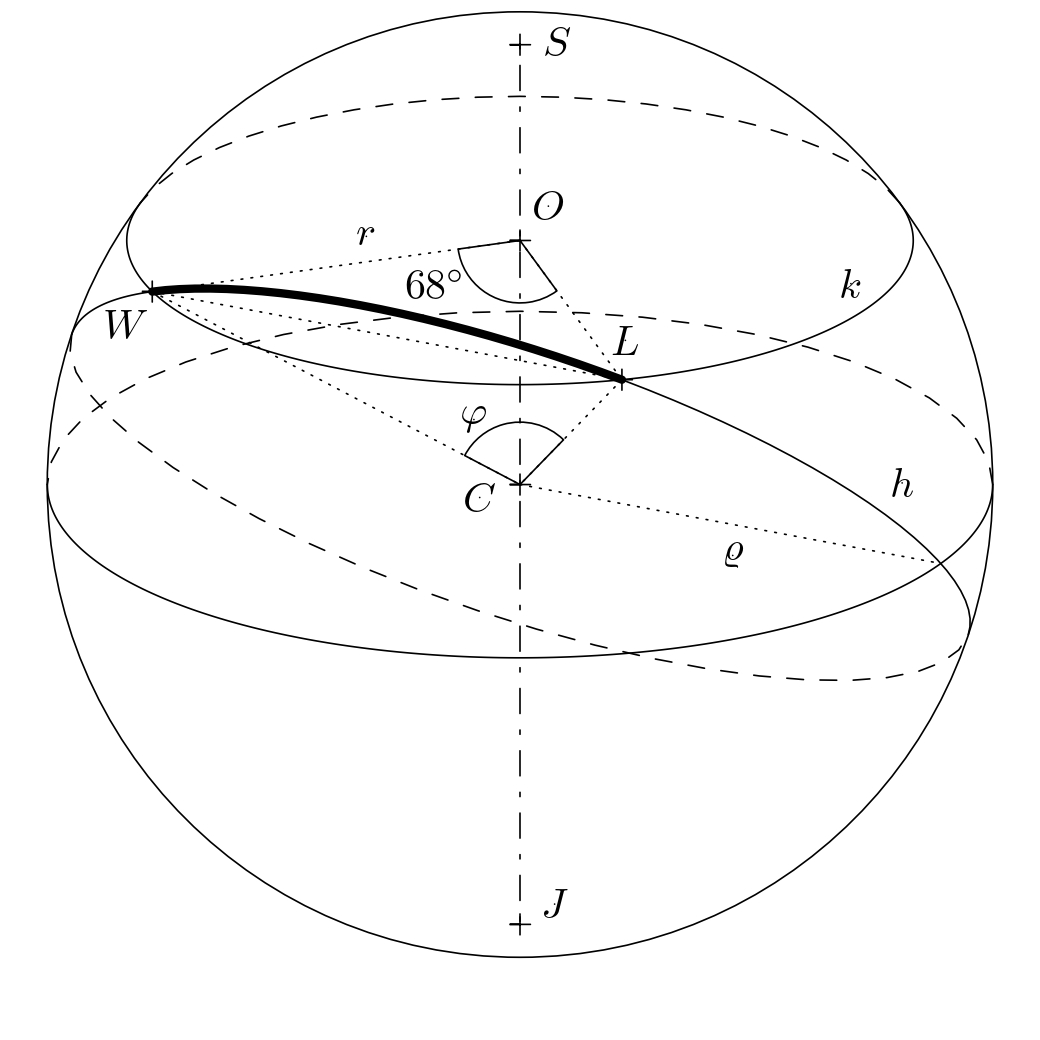
Let us consider an isosceles triangle \(OWL\), which we bisect with the height to the base \(LW\) into two congruent right triangles. In either of these two triangles, then the equation \(\frac{|LW|}{2}=r\cdot \sin 34^{\circ}\) holds, and thus \(|LW|=2r\cdot\sin 34^{\circ}\). If we follow similar reasoning for the isosceles triangle \(CWL\), we get the equality \(|LW|=2\varrho \cdot \sin\frac{\varphi}{2}\). By comparing the right sides of both derived equalities, we calculate the required angle \(\varphi\):
\[ 2r\sin34^{\circ} = 2\varrho \sin\frac{\varphi}{2} \]
\[ \sin\frac{\varphi}{2} = \frac{r\sin34^{\circ}}{\varrho} = \frac{\varrho \cos39^{\circ}\sin 34^{\circ}}{\varrho} = \cos 39^{\circ}\sin 34^{\circ} \]
\[ \frac{\varphi}{2}= \arcsin \left( \cos 39^{\circ}\sin 34^{\circ} \right) \doteq 25^{\circ}45' \quad \Rightarrow \quad \varphi \doteq 51^{\circ}30'. \]
We determine the trajectory of the airplane traveling along the orthodrome similarly as in the case of a parallel line using direct proportion. The length of the whole circle \(h\) is equal to \(2\pi\varrho\). Then, for the length of the shorter arc \(LW\), the following calculation applies
\[ \frac{51{,}5}{360}\cdot 2\pi\varrho \doteq 5,735{.}5 \,\text{km}. \]
We see that the two trajectories differ by approximately \(150 \,\text{km}\).
