Která z cest mezi Lisabonem a Washingtonem znázorněných na mapě je kratší?
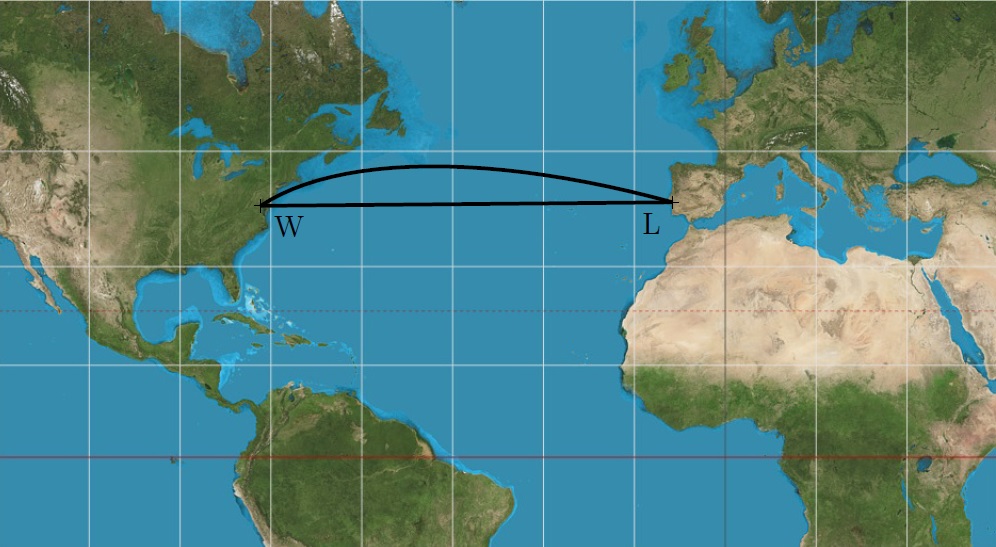
Zdánlivě jednoduchý dotaz má, jak si ověříte v této úloze, překvapivou odpověď. Kratší trasa je oblouk, delší je úsečka. Důvodem je zkreslení vzdáleností ve zvoleném zobrazení zemského povrchu. Vidíme, že úsečka \(LW\) na mapě je přibližně rovnoběžná s geografickými rovnoběžkami na Zemi, tedy ve skutečnosti odpovídá oblouku na kružnici, která se velmi podobá rovnoběžce (viz kružnice \(k\) se středem \(O\) na obrázku).
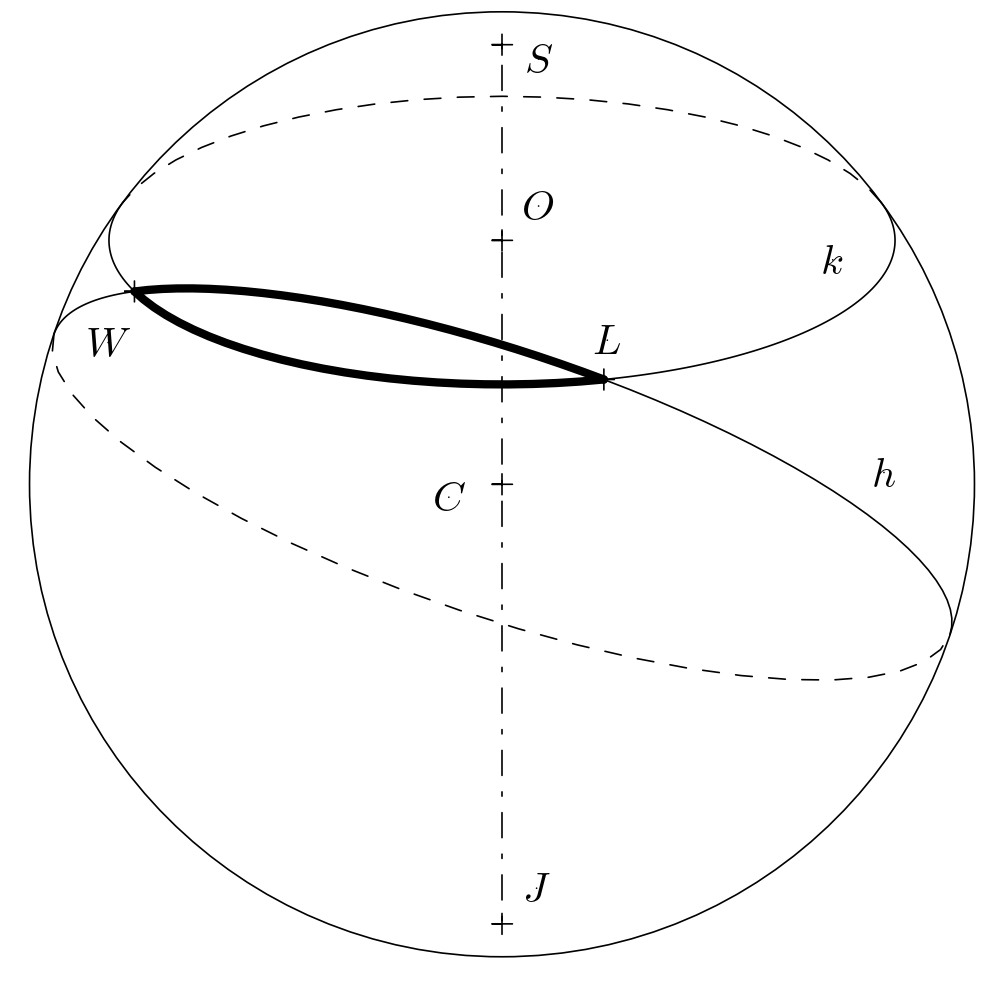
Na kulovém povrchu (který budeme v této úloze považovat za povrch Země) je však nejkratší vzdálenost jiný oblouk. Tento oblouk leží na kružnici \(h\), jejíž střed \(C\) je středem Země. Takové spojnice označujeme jako ortodromy a všechny kružnice s uvedenou vlastností nazýváme hlavními kružnicemi. O kolik kilometrů si však cestou po ortodromě polepšíme? Odpověď na tuto otázku je již potřeba spočítat.
Úloha. Lisabon i Washington se nachází přibližně na stejné rovnoběžce (asi \(39^{\circ}\) severní šířky). O kolik kilometrů méně uletí letadlo pohybující se po ortodromě oproti cestě po rovnoběžce? Lisabon se nachází na přibližně \(9^{\circ}\) západní délky, Washington na \(77^{\circ}\) západní délky. Předpokládejme, že je Země koulí se středem \(C\) a poloměrem \(6\ 371\,\text{km}\) a že letadlo letí v průměrné výšce \(10\,\text{km}\) (vzlet a přistání brát do úvahy nebudeme). Proto budeme ve všech úvahách pracovat s koulí o poloměru \(\varrho=6\ 381\,\text{km}\).
Řešení. Určeme nejdříve, kolik kilometrů urazí letadlo při cestě po rovnoběžce. Označme rovnoběžku na \(39^{\circ}\) severní šířky jako kružnici \(k\) se středem \(O\) a poloměrem \(r\). Ve vhodném pravoúhlém průmětu zeměkoule (viz obrázek, kde \(S\) a \(J\) jsou póly) se řečená kružnice zobrazí jako úsečka \(AB\) se středem \(O\).
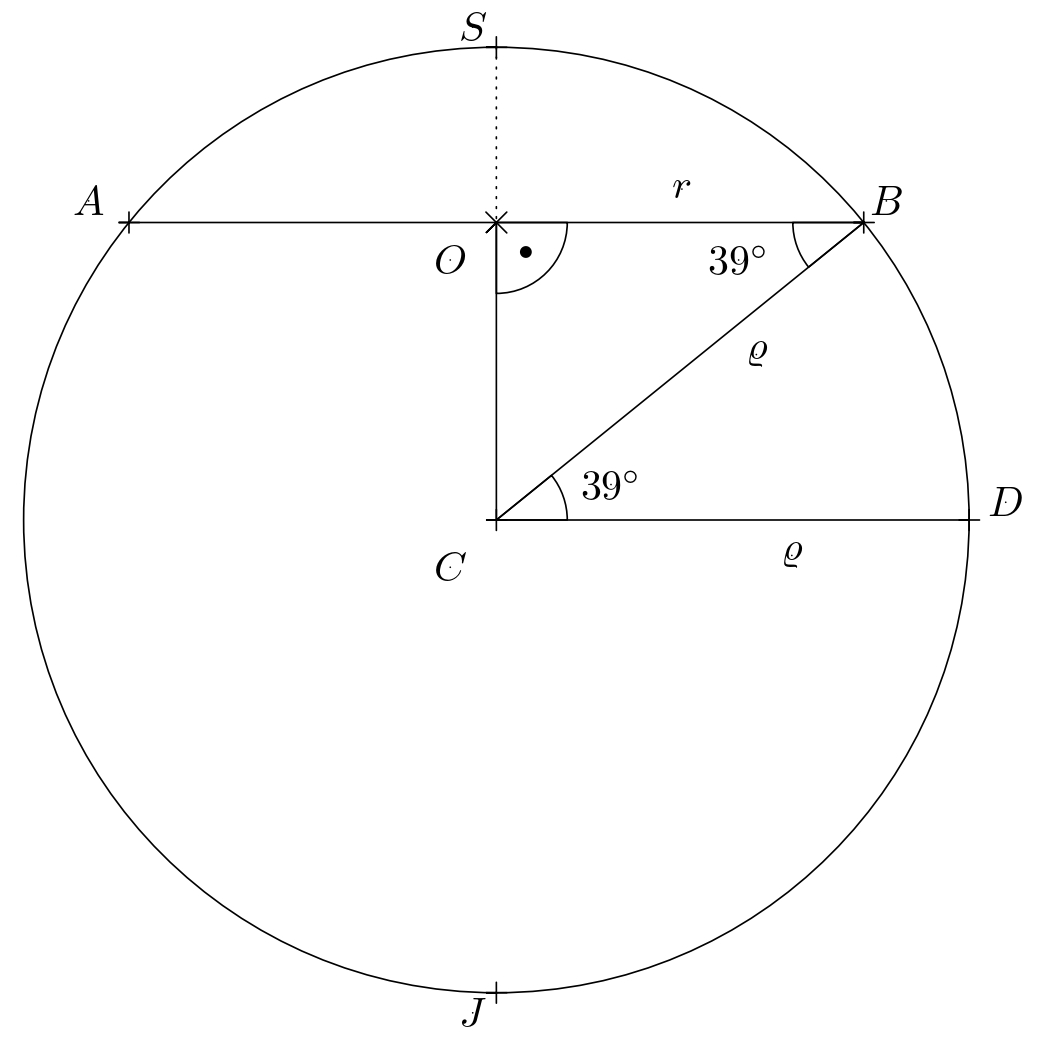
Z obrázku je zřejmá rovnost \(\lvert\sphericalangle CBO\rvert = \lvert\sphericalangle BCD\rvert\) (úhly jsou střídavé) a užitím funkce kosinus v pravoúhlém trojúhelníku \(BSO\) dostáváme \(r=\varrho\cdot \cos 39^{\circ}\).
Dráhu letadla pohybujícího se po rovnoběžce (v obrázku níže je trajektorie letadla znázorněná kratším obloukem \(LW\)) určíme přímou úměrou. Celá kružnice \(k\) má délku \(2\pi r =2\pi\varrho\cdot\cos 39^{\circ} \,\text{km}\), tedy délka kratšího oblouku \(LW\) je rovna \[ \frac{(77-9)}{360}\cdot 2\pi\varrho\cdot \cos 39^{\circ} \doteq 5\ 885{,}4\,\text{km}. \]
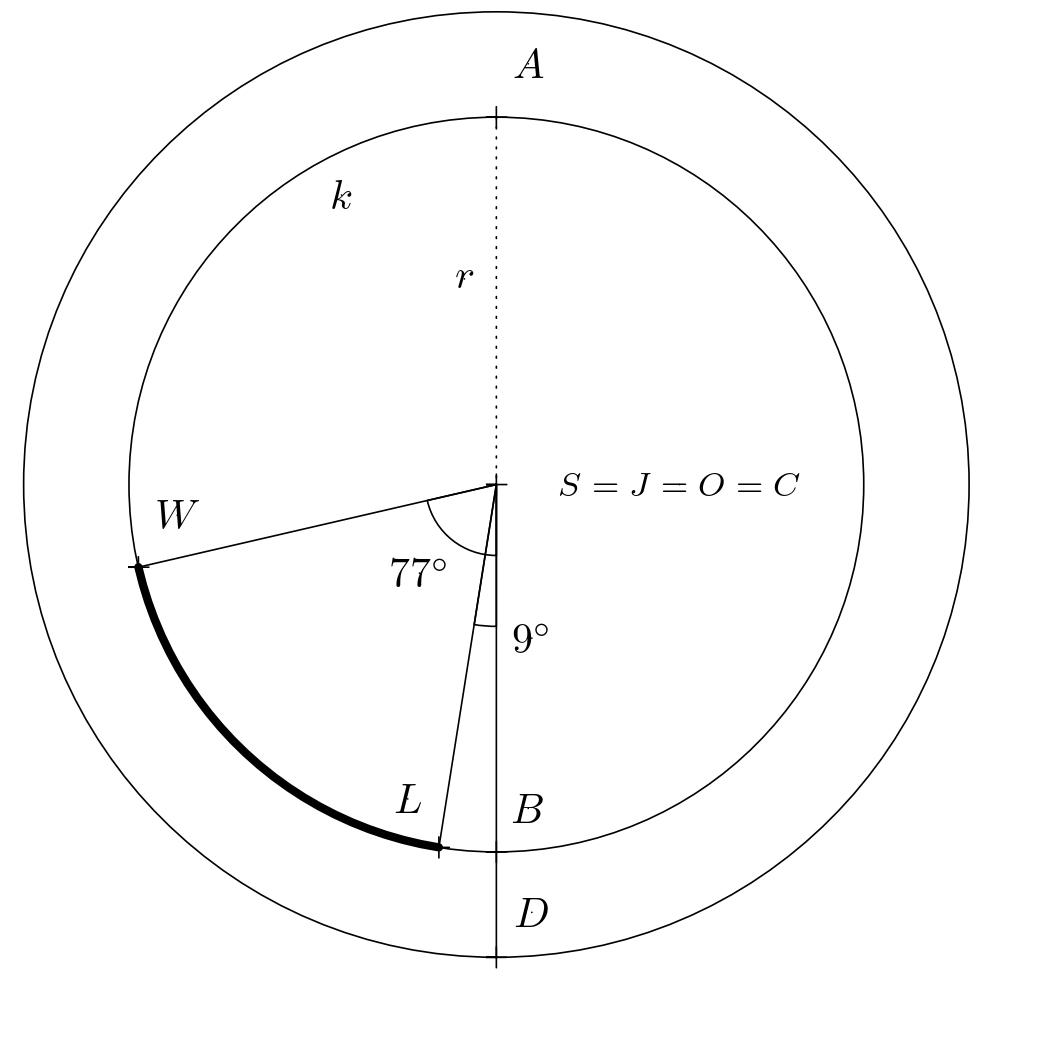
Nyní zjistíme, kolik kilometrů uletí letadlo pohybující se po ortodromě. Jedná se vlastně o vzdálenost dvou bodů na pomyslné sféře o poloměru \(\varrho=6\ 381\,\text{km}\). Na obrázku lze vidět, že ortodroma mezi body \(L\) a \(W\) je obloukem jisté hlavní kružnice \(h\) s neznámým středovým úhlem \(\varphi\). Tento úhel musíme určit.
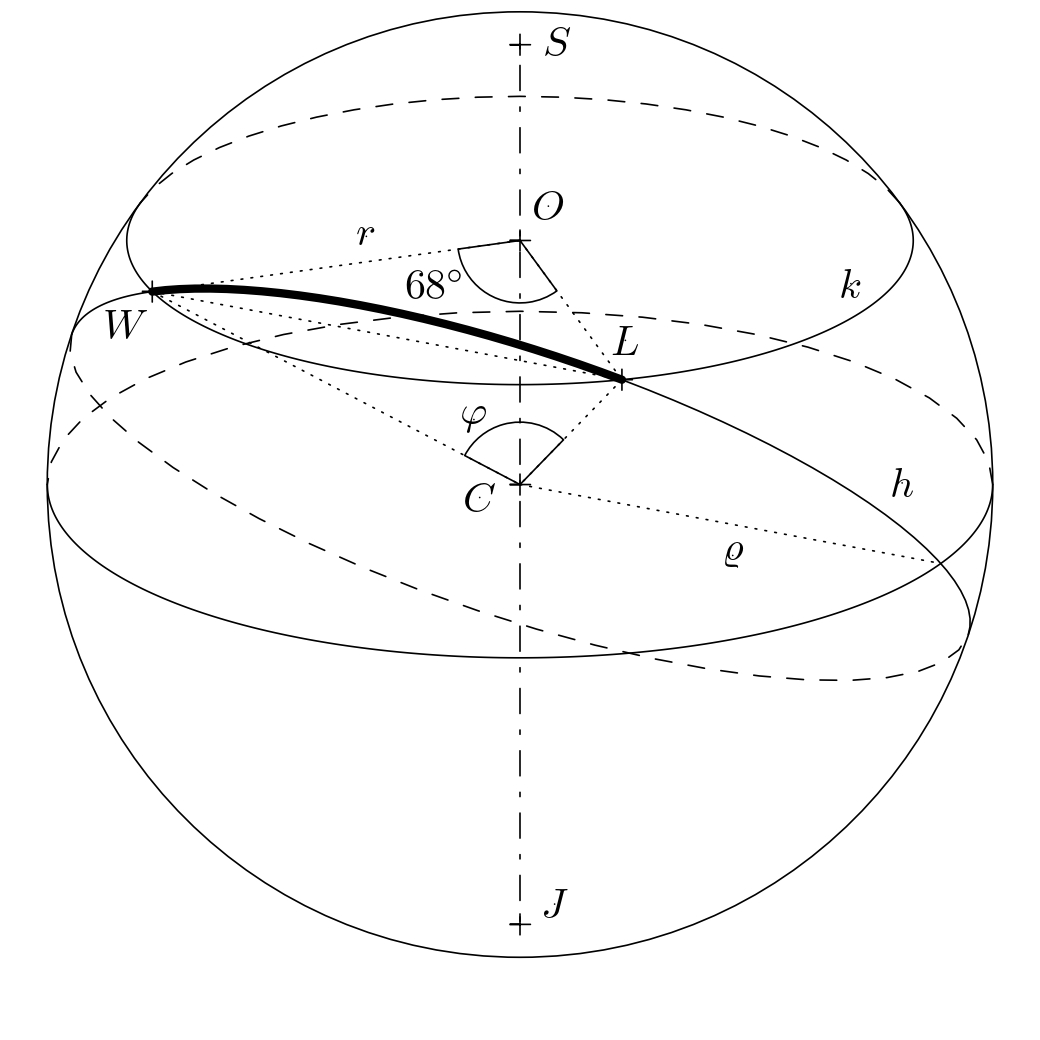
Uvažme rovnoramenný trojúhelník \(OWL\), který rozpůlíme výškou na základnu \(LW\) na dva shodné pravoúhlé trojúhelníky. V libovolném z těchto dvou trojúhelníků pak platí \(\frac{|LW|}{2}=r\cdot \sin 34^{\circ}\), a tedy \(|LW|=2r\cdot\sin 34^{\circ}\). Pokud provedeme podobnou úvahu pro rovnoramenný trojúhelník \(CWL\), dostáváme rovnost \(|LW|=2\varrho \cdot \sin\frac{\varphi}{2}\). Porovnáním pravých stran obou odvozených rovností vypočítáme hledaný úhel \(\varphi\):
\[ 2r\sin34^{\circ} = 2\varrho \sin\frac{\varphi}{2} \]
\[ \sin\frac{\varphi}{2} = \frac{r\sin34^{\circ}}{\varrho} = \frac{\varrho \cos39^{\circ}\sin 34^{\circ}}{\varrho} = \cos 39^{\circ}\sin 34^{\circ} \]
\[ \frac{\varphi}{2}= \arcsin \left( \cos 39^{\circ}\sin 34^{\circ} \right) \doteq 25^{\circ}45' \quad \Rightarrow \quad \varphi \doteq 51^{\circ}30'. \]
Dráhu letadla pohybujícího se po ortodromě určíme podobně jako v případě rovnoběžky přímou úměrou. Délka celé kružnice \(h\) je rovna \(2\pi\varrho\), pro délku kratšího oblouku \(LW\) pak platí
\[ \frac{51{,}5}{360}\cdot 2\pi\varrho \doteq 5\ 735{,}5 \,\text{km}. \]
Vidíme, že se obě dráhy liší přibližně o \(150 \,\text{km}\).
