¿Cuál de las rutas entre Lisboa y Washington que se muestran en el mapa es más corta?
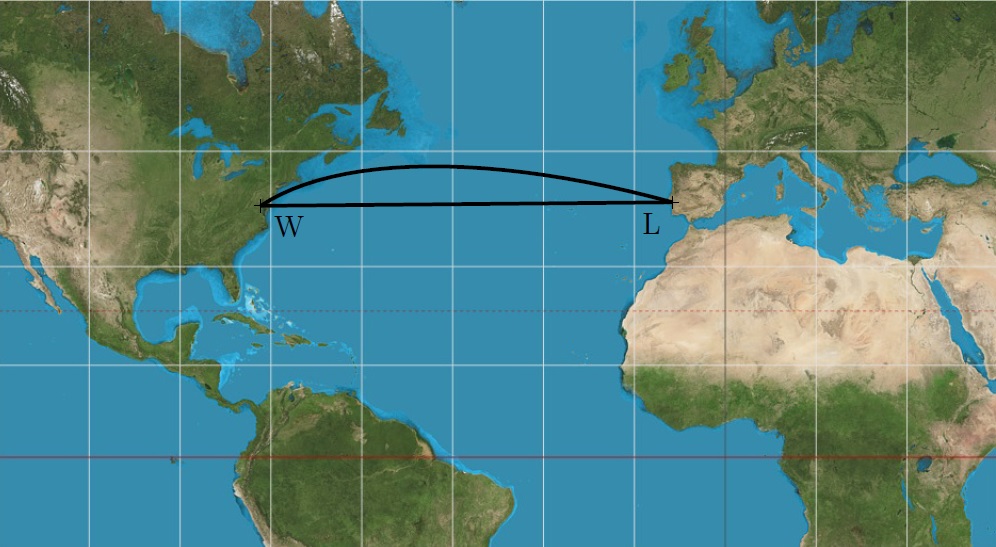
Esta pregunta aparentemente sencilla tiene una respuesta sorprendente, como verás en este ejercicio. La ruta más corta es el arco, la más larga es el segmento de línea. La razón es la distorsión de las distancias en la representación seleccionada de la superficie terrestre. Vemos que el segmento de línea \(LW\) en el mapa es aproximadamente paralelo a los paralelos geográficos de la Tierra, por lo que en realidad corresponde a un arco de un círculo que se asemeja mucho a un paralelo (ver el círculo \(k\) con centro \(O\) en la figura).
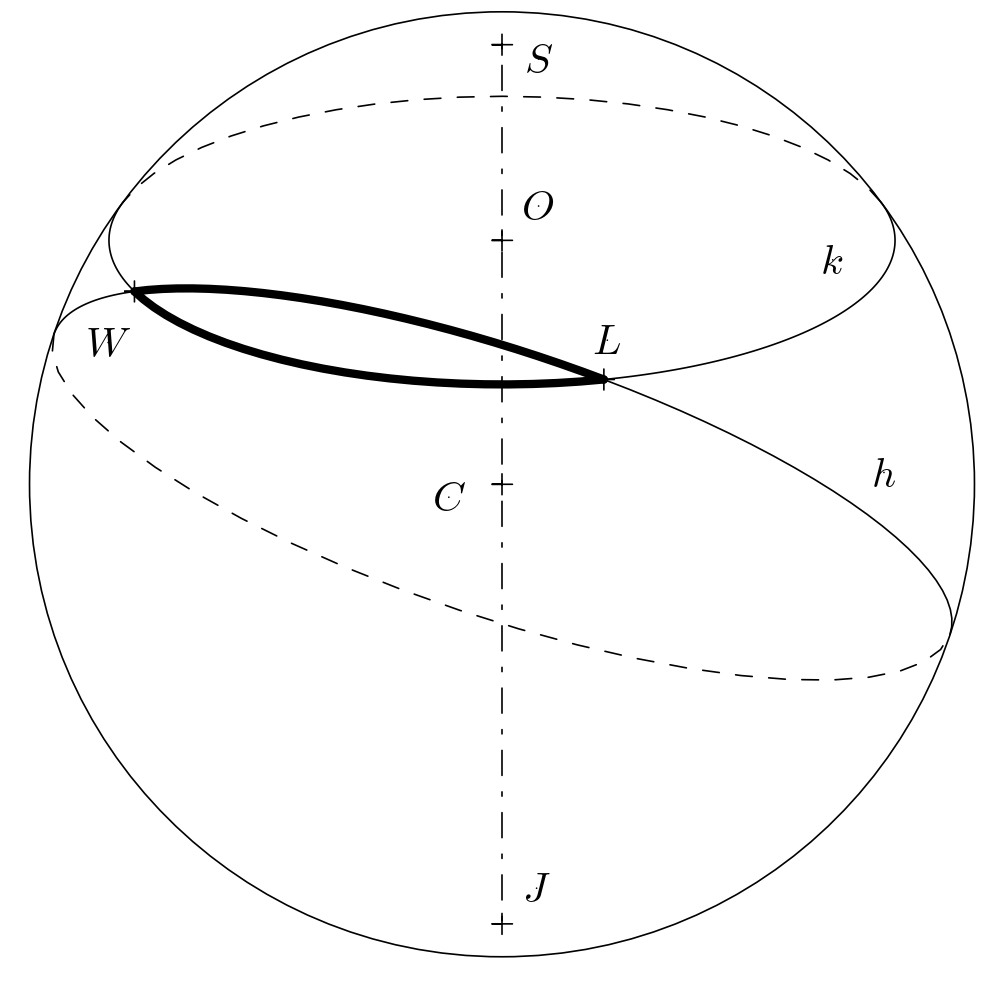
Sin embargo, en la superficie esférica (que en esta tarea consideraremos como la superficie de la Tierra), la distancia más corta es otro arco. Este arco forma parte de un círculo \(h\) cuyo centro \(C\) es el centro de la Tierra. A este tipo de trayectos los llamamos ortodromias y llamamos círculos máximos a todos los círculos con esta propiedad. ¿Cuántos kilómetros se ahorran al viajar por una ortodromia? La respuesta a esta pregunta debe calcularse.
Ejercicio. Lisboa y Washington están ubicadas aproximadamente en el mismo paralelo (unos \(39^{\circ}\) de latitud norte). ¿Cuántos kilómetros ahorra un avión al viajar por una trayectoria ortodrómica en comparación con una trayectoria por el paralelo? Lisboa se encuentra aproximadamente en la longitud oeste de \(9^{\circ}\). Washington está ubicada en la longitud oeste de \(77^{\circ}\). Supongamos que la Tierra es una esfera con centro \(C\) y radio \(6,371,\text{km}\), y que el avión vuela a una altitud media de \(10,\text{km}\) (no se tienen en cuenta el despegue y el aterrizaje). Por lo tanto, en todas las consideraciones, trabajaremos con una esfera de radio \(\varrho = 6,381,\text{km}\).
Solución. Primero, determinemos cuántos kilómetros recorrerá el avión al viajar a lo largo del paralelo. Denotemos el paralelo a \(39^{\circ}\) de latitud norte como un círculo \(k\) con centro \(O\) y radio \(r\). En una proyección ortogonal apropiada del globo (véase la figura, donde \(S\) y \(J\) son los polos), este círculo aparece como una cuerda \(AB\) con centro \(O\).
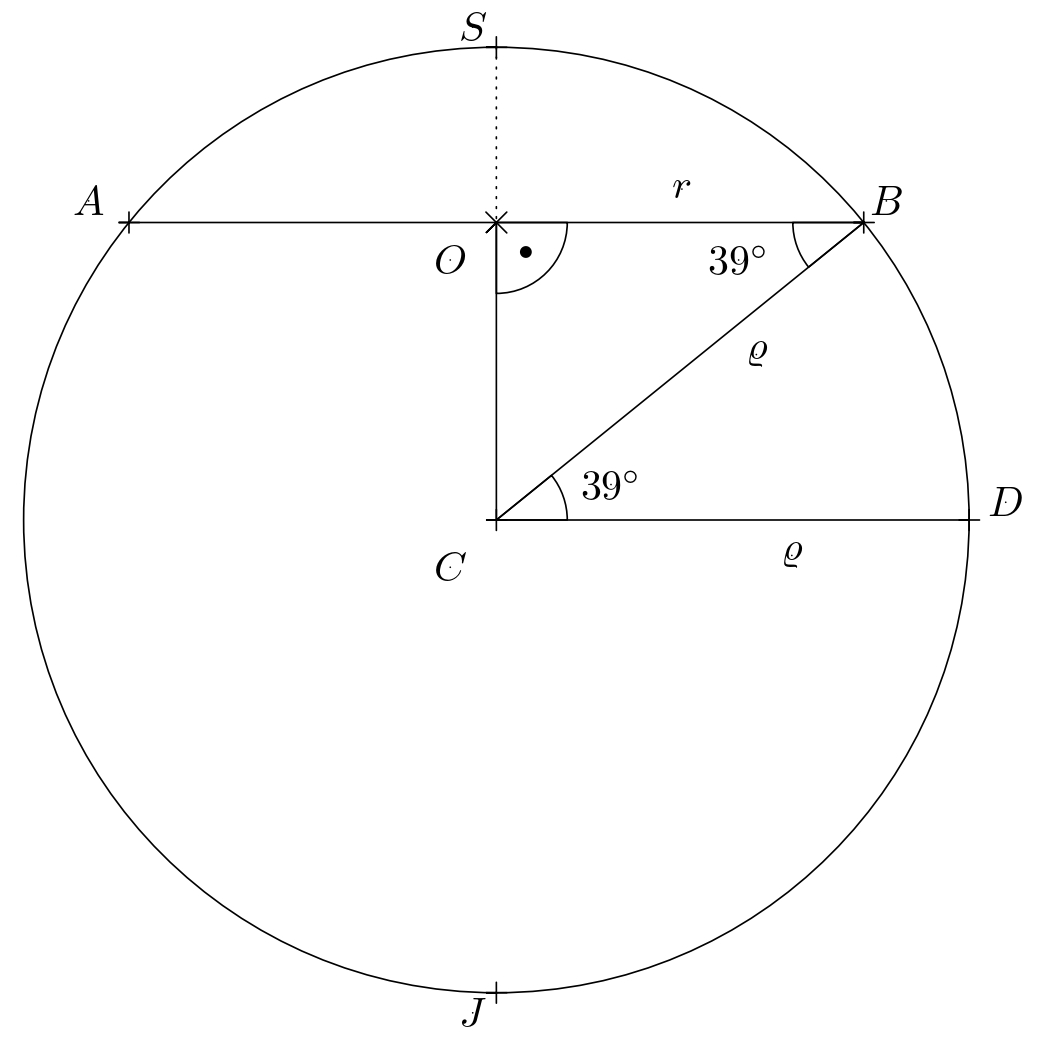
La figura muestra la igualdad \(\lvert\sphericalangle CBO\rvert = \lvert\sphericalangle BCD\rvert\) (los ángulos son alternos) y, utilizando la función coseno en el triángulo rectángulo \(BSO\), obtenemos que \(r = \varrho \cdot \cos 39^{\circ}\).
La trayectoria del avión que se mueve a lo largo del paralelo (en la figura de abajo, la trayectoria del avión está representada por el arco más corto \(LW\)) se determina utilizando una proporción directa: el círculo completo \(k\) tiene una longitud de \(2\pi r = 2\pi\varrho \cdot \cos 39^{\circ} ,\text{km}\), es decir, la longitud del arco más corto \(LW\) es igual a \[ \frac{(77-9)}{360}\cdot 2\pi\varrho\cdot \cos 39^{\circ} \doteq 5,885{.}4\,\text{km}. \]
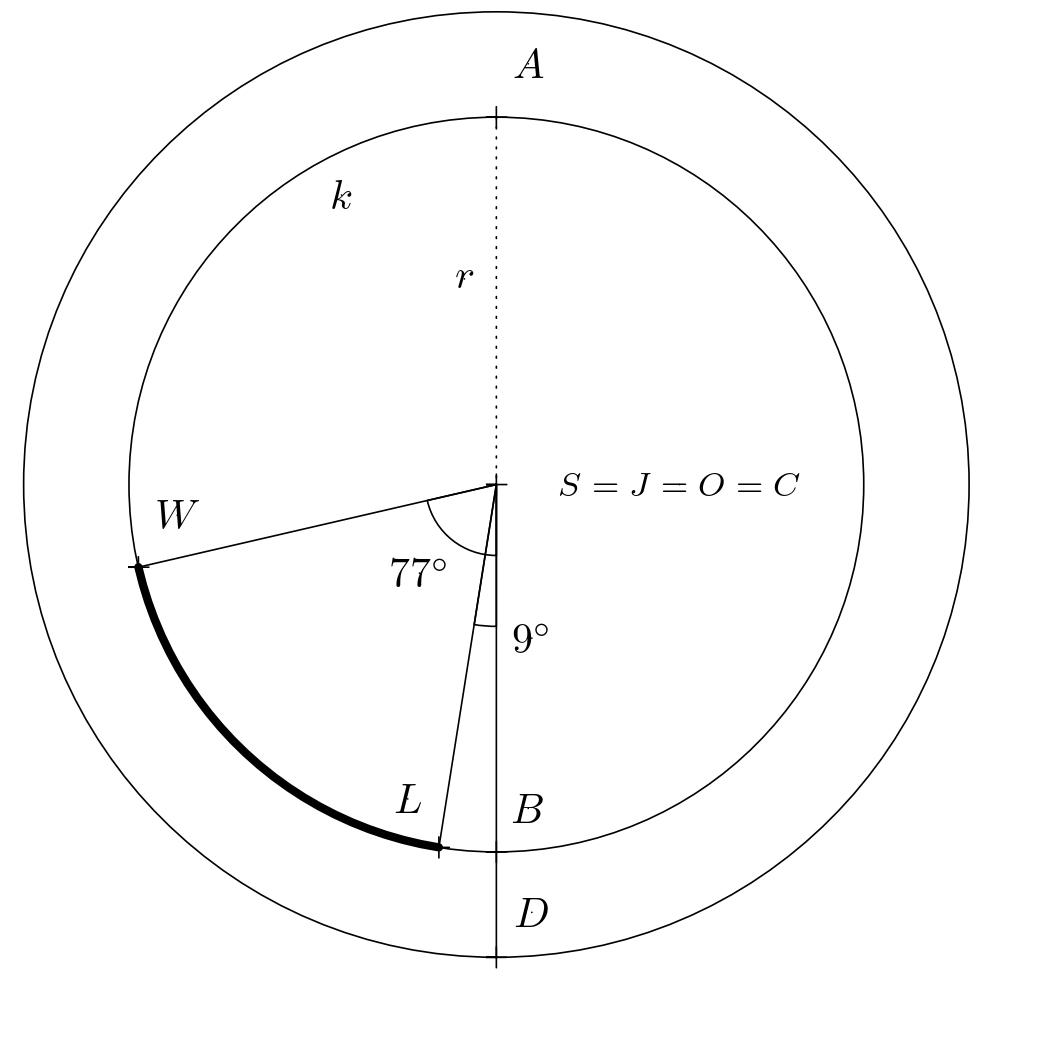
Ahora determinamos cuántos kilómetros recorre el avión al desplazarse por la ortodromia. Esta es esencialmente la distancia entre dos puntos sobre una esfera imaginaria con radio \(\varrho = 6,381,\text{km}\). La figura muestra que la ortodromia entre los puntos \(L\) y \(W\) es un arco de cierto círculo máximo \(h\) con un ángulo central desconocido \(\varphi\). Necesitamos determinar la medida de este ángulo.
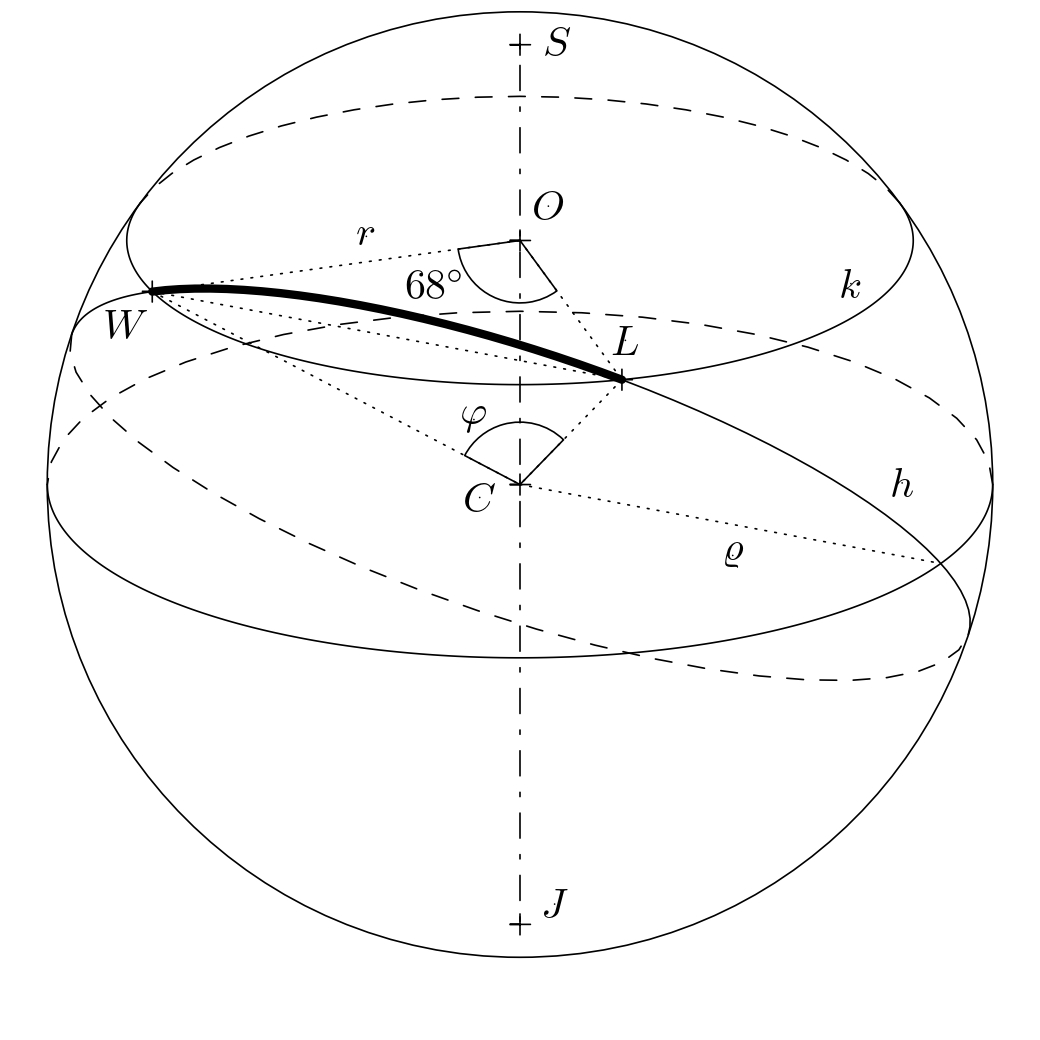
Consideremos un triángulo isósceles \(OWL\), que dividimos por la altura trazada a la base \(LW\) en dos triángulos rectángulos congruentes. En cualquiera de estos dos triángulos, se cumple la ecuación \(\frac{|LW|}{2} = r \cdot \sin 34^{\circ}\), y por lo tanto \(|LW| = 2r \cdot \sin 34^{\circ}\). Si seguimos un razonamiento similar para el triángulo isósceles \(CWL\), obtenemos la igualdad \(|LW| = 2\varrho \cdot \sin \frac{\varphi}{2}\). Al comparar los lados derechos de ambas igualdades derivadas, calculamos el ángulo requerido \(\varphi\):
\[ 2r\sin34^{\circ} = 2\varrho \sin\frac{\varphi}{2} \]
\[ \sin\frac{\varphi}{2} = \frac{r\sin34^{\circ}}{\varrho} = \frac{\varrho \cos39^{\circ}\sin 34^{\circ}}{\varrho} = \cos 39^{\circ}\sin 34^{\circ} \]
\[ \frac{\varphi}{2}= \arcsin \left( \cos 39^{\circ}\sin 34^{\circ} \right) \doteq 25^{\circ}45' \quad \Rightarrow \quad \varphi \doteq 51^{\circ}30'. \]
Determinamos la trayectoria del avión que viaja por la ortodromia de manera similar a como lo hicimos en el caso del paralelo, utilizando una proporción directa. La longitud del círculo completo \(h\) es igual a \(2\pi\varrho\). Entonces, para la longitud del arco más corto \(LW\), se aplica el siguiente cálculo:
\[ \frac{51{,}5}{360}\cdot 2\pi\varrho \doteq 5,735{.}5 \,\text{km}. \]
Vemos que las dos trayectorias difieren en aproximadamente \(150 \,\text{km}\).
