Która z tras między Lizboną a Waszyngtonem pokazanych na mapie jest krótsza?
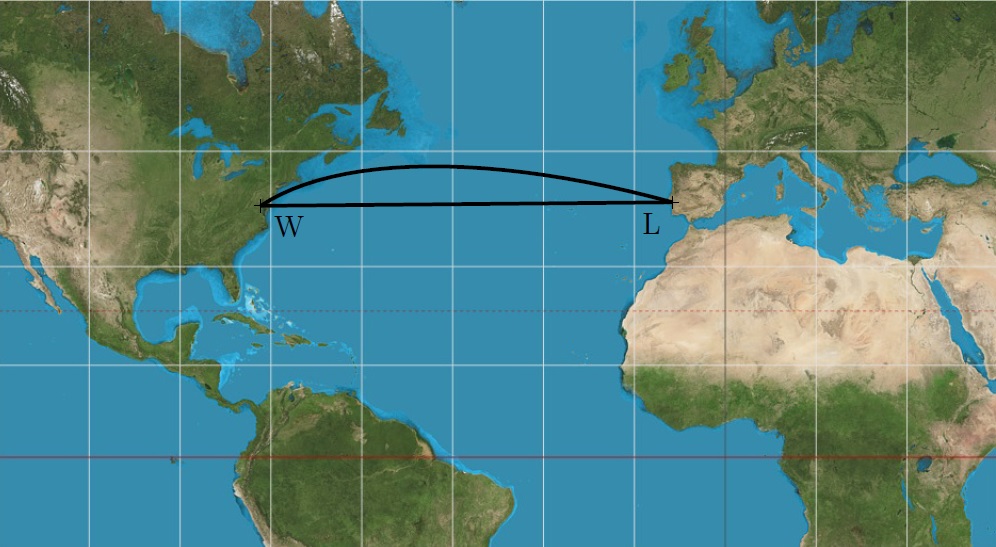
To pozornie proste pytanie ma zaskakującą odpowiedź, o czym przekonasz się w tym ćwiczeniu. Krótsza trasa to łuk, a dłuższa to odcinek linii. Powodem jest zniekształcenie odległości w wybranej reprezentacji powierzchni Ziemi. Widzimy, że odcinek linii \(LW\) na mapie jest w przybliżeniu równoległy do równoleżników geograficznych na Ziemi, więc w rzeczywistości odpowiada łukowi na okręgu, który bardzo przypomina równoleżnik. (patrz okrąg \(k\) ze środkiem \(O\) na rysunku).
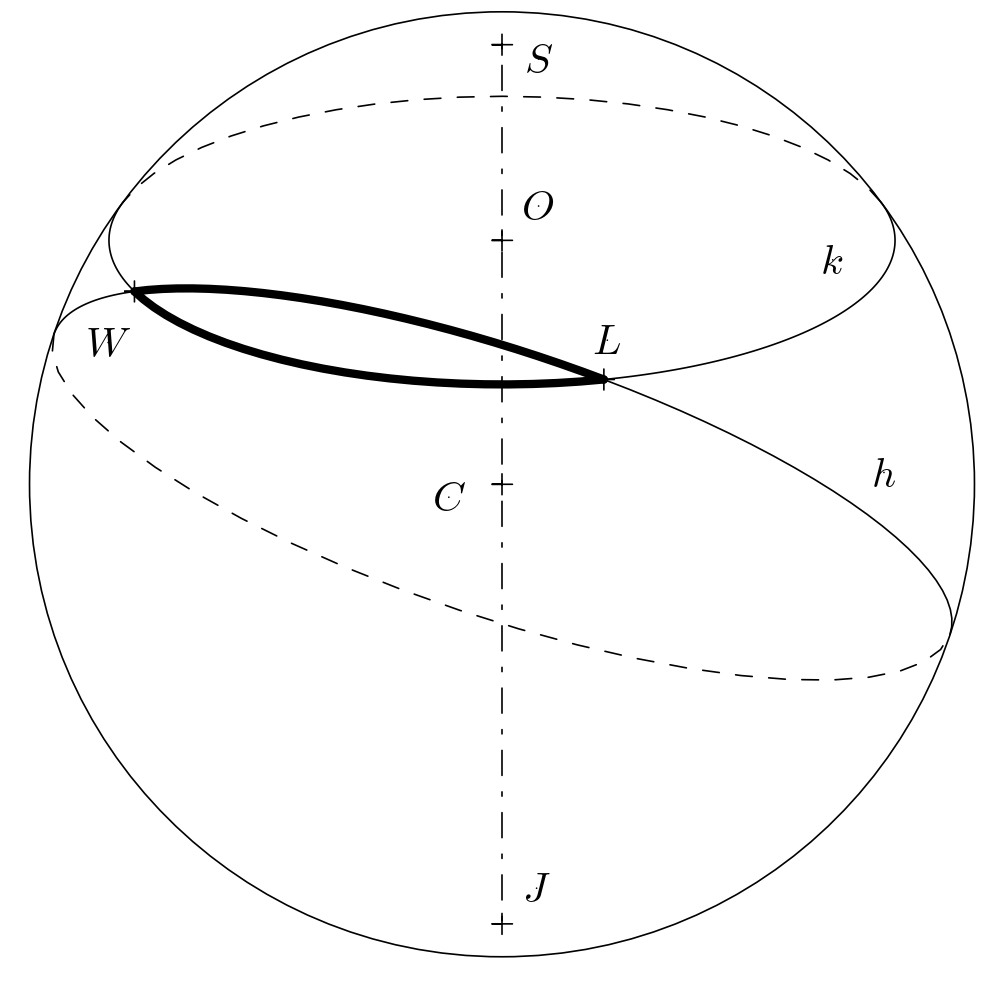
Jednak na powierzchni kulistej (którą w tym zadaniu uznamy za powierzchnię Ziemi), najkrótszą odległością jest inny łuk. Łuk ten jest częścią okręgu \(h\), którego środkiem \(C\) jest środek Ziemi. Odnosimy się do takich ścieżek jako ortodromy i nazywamy wszystkie okręgi z tą właściwością wielkimi okręgami. Ile kilometrów zaoszczędzimy podróżując wzdłuż ortodromy? Odpowiedź na to pytanie należy obliczyć.
Szerokość geograficzna punktu na powierzchni Ziemi (wyrażona w stopniach i orientacji północ/południe) to kąt pomiędzy linią prostą przechodzącą przez dany punkt a środkiem Ziemi i płaszczyzną równika. Długość geograficzna punktu na powierzchni Ziemi (wyrażona w stopniach i orientacji wschód / zachód) to kąt między płaszczyzną południka przechodzącego przez dany punkt a płaszczyzną południka zerowego.
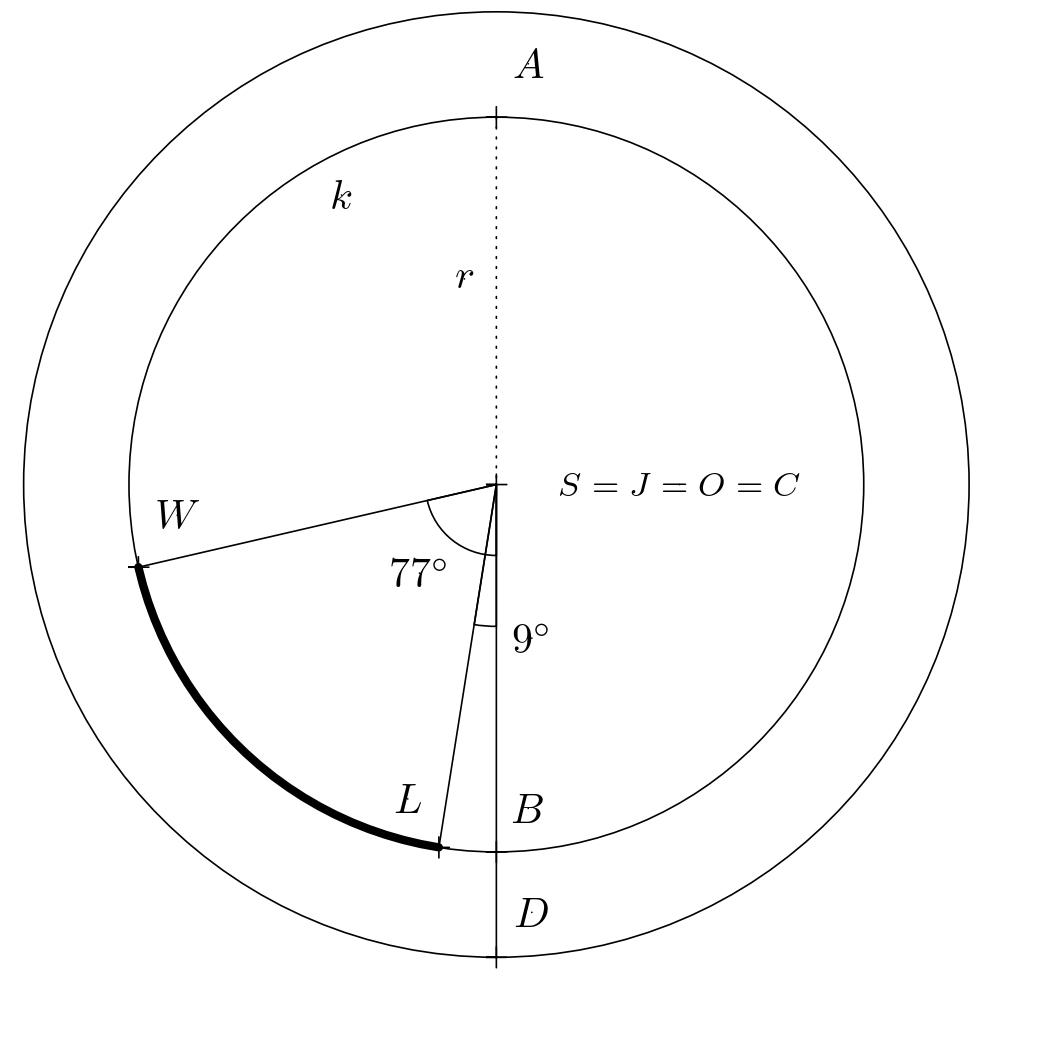
**Lizbona i Waszyngton znajdują się mniej więcej na tym samym równoleżniku w przybliżeniu na tym samym równoleżniku (ok. \(39^{\circ}\) szerokości geograficznej północnej). Ile kilometrów oszczędza samolot podróżując ścieżką ortodromiczną w porównaniu do podróży ścieżką równoległą? Lizbona jest położona na wysokości ok. \(9^{\circ}\) długości geograficznej zachodniej. Waszyngton znajduje się pod \(77^{\circ}\) długości zachodniej. Załóżmy, że Ziemia jest kulą o środku \(C\) i promieniu \(6,371\,\text{km}\) i że samolot leci na średniej wysokości \(10\,\text{km}\) (start i lądowanie nie są brane pod uwagę). Dlatego we wszystkich rozważaniach będziemy pracować z kulą o promieniu \(\varrho=6,381\,\text{km}\).
Rozwiązanie: Najpierw określmy, ile kilometrów pokona samolot, podróżując wzdłuż równoleżnika. Oznaczmy równoleżnik jako \(39^{\circ}\) szerokość geograficzna północna jako okrąg \(k\) ze środkiem \(O\) i promień \(r\). W odpowiednim rzucie ortogonalnym kuli ziemskiej (patrz rysunek, gdzie \(S\) i \(J\) są biegunami), okrąg ten jest cięciwą \(AB\) o środku \(O\).
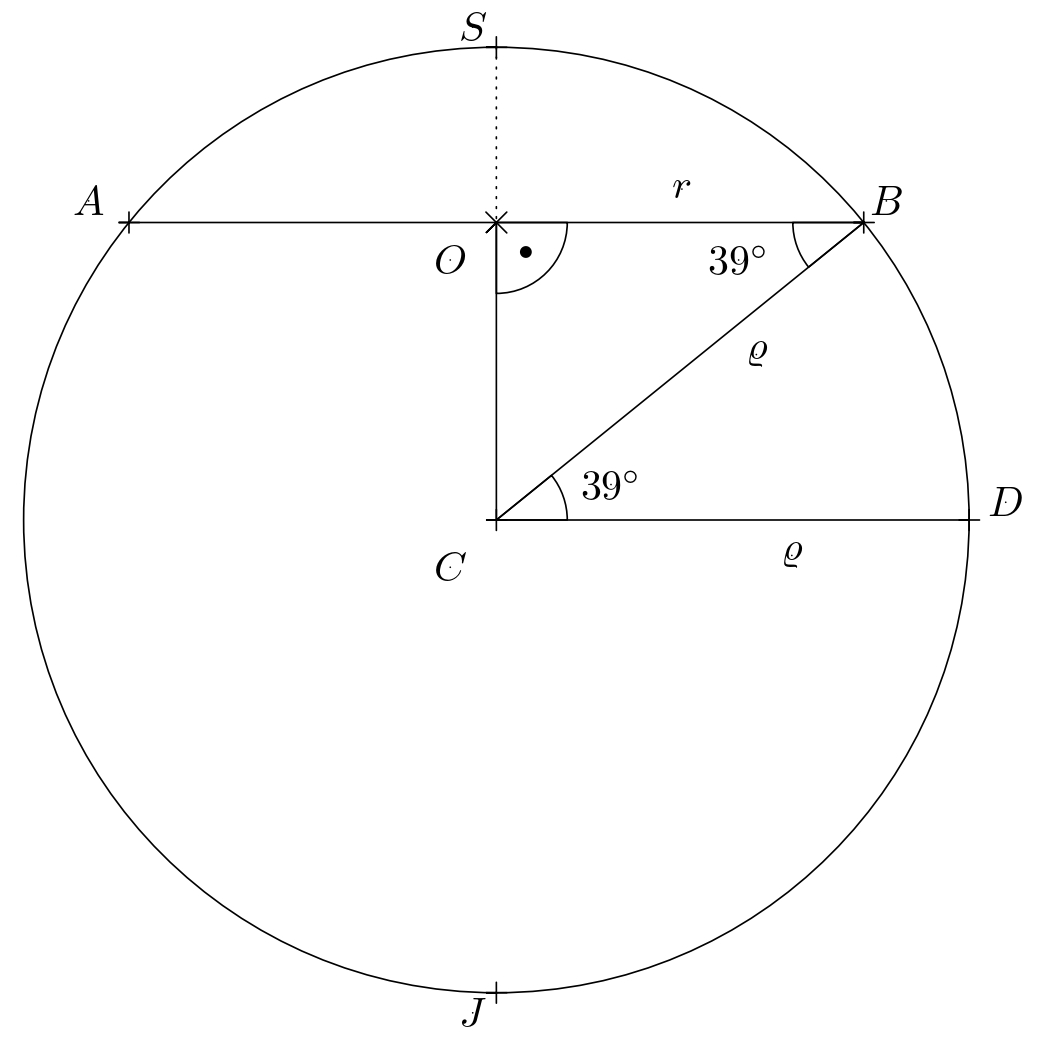
Rysunek przedstawia równość \(\lvert\sphericalangle CBO\rvert = \lvert\sphericalangle BCD\rvert\) (kąty są naprzemienne) i używając funkcji cosinus w trójkącie prostokątnym \(BSO\) otrzymujemy \(r=\varrho\cdot \cos 39^{\circ}\).
Trajektoria samolotu poruszającego się wzdłuż równoleżnika (na poniższym rysunku, trajektoria samolotu jest reprezentowana przez krótszy łuk \(LW\)) jest określana przy użyciu bezpośredniej proporcji: cały okrąg \(k\) ma długość \(2\pi r =2\pi\varrho\cdot\cos 39^{\circ} \,\text{km}\), tzn. długość krótszego łuku \(LW\) jest równa \[ \frac{(77-9)}{360}\cdot 2\pi\varrho\cdot \cos 39^{\circ} \doteq 5,885{.}4\,\text{km}. \]
Teraz określamy, ile kilometrów pokonuje samolot, poruszając się wzdłuż ortodromy. Jest to zasadniczo odległość między dwoma punktami na wyimaginowanej kuli o promieniu \(\varrho=6,381\,\text{km}\). Rysunek pokazuje, że ortodroma między punktami \(L\) i \(W\) jest łukiem pewnego koła wielkiego \(h\) o nieznanym kącie środkowym \(\varphi\). Musimy określić miarę tego kąta.
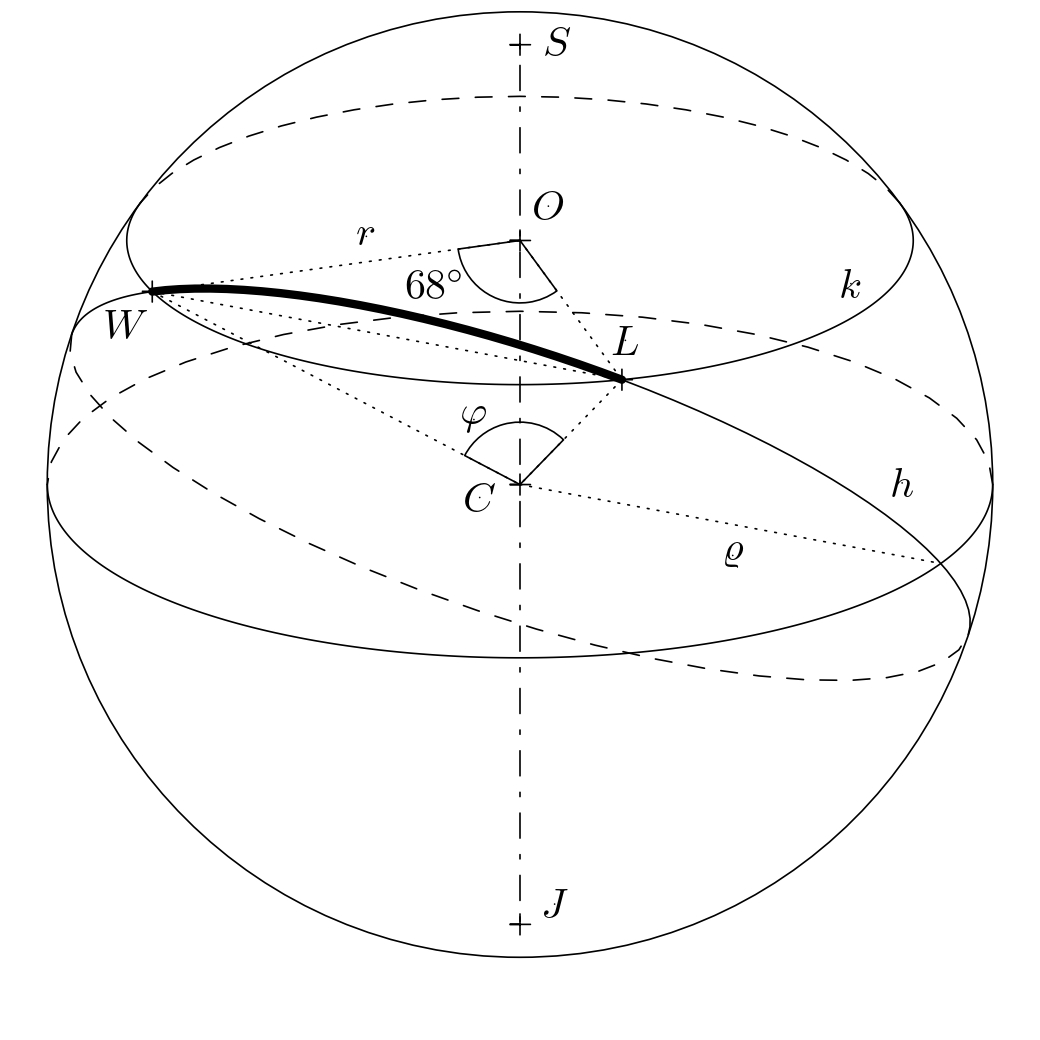
Rozważmy trójkąt równoramienny \(OWL\), który podzielimy wysokością na podstawę \(LW\) na dwa przystające trójkąty prostokątne. W każdym z tych dwóch trójkątów zachodzi równanie \(\frac{|LW|}{2}=r\cdot \sin 34^{\circ}\) utrzymuje, a zatem \(|LW|=2r\cdot\sin 34^{\circ}\). Jeśli zastosujemy podobne rozumowanie dla trójkąta równoramiennego \(CWL\), otrzymujemy równość \(|LW|=2\varrho \cdot \sin\frac{\varphi}{2}\). Porównując prawe strony obu wyprowadzonych równości, obliczamy wymagany kąt \(\varphi\):
\[ 2r\sin34^{\circ} = 2\varrho \sin\frac{\varphi}{2} \]
\[ \sin\frac{\varphi}{2} = \frac{r\sin34^{\circ}}{\varrho} = \frac{\varrho \cos39^{\circ}\sin 34^{\circ}}{\varrho} = \cos 39^{\circ}\sin 34^{\circ} \]
\[ \frac{\varphi}{2}= \arcsin \left( \cos 39^{\circ}\sin 34^{\circ} \right) \doteq 25^{\circ}45' \quad \Rightarrow \quad \varphi \doteq 51^{\circ}30'. \]
Wyznaczamy trajektorię samolotu poruszającego się wzdłuż ortodromy w podobny sposób jak w przypadku linii równoległej, korzystając z proporcji bezpośredniej. Długość całego okręgu \(h\) jest równa \(2\pi\varrho\). Następnie, dla długości krótszego łuku \(LW\), stosuje się następujące obliczenia
\[ \frac{51{,}5}{360}\cdot 2\pi\varrho \doteq 5,735{.}5 \,\text{km}. \]
Widzimy, że obie trajektorie różnią się o ok. \(150 \,\text{km}\).
