Ktorá z trás medzi Lisabonom a Washingtonom zobrazených na mape je kratšia?
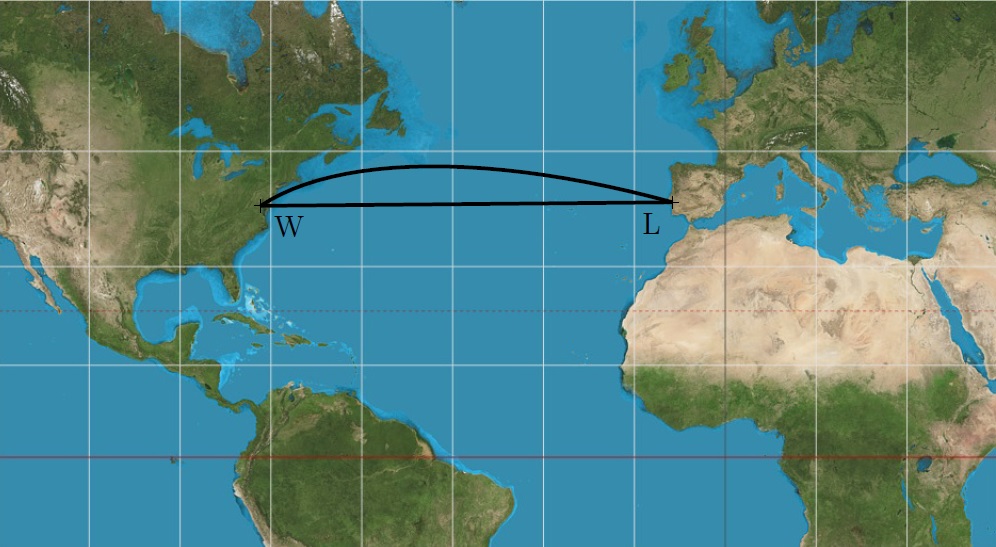
V tejto úlohe uvidíte, že táto zdanlivo jednoduchá otázka má prekvapujúcu odpoveď. Kratšia trasa je oblúk a dlhšia je úsečka. Dôvodom je skreslenie vzdialeností vo zvolenom zobrazení zemského povrchu. Vidíme, že úsečka \(LW\) na mape je približne rovnobežná s geografickými rovnobežkami na Zemi. V skutočnosti teda zodpovedá oblúku na kružnici a veľmi sa podobá rovnobežke (pozri kružnicu \(k\) so stredom \(O\) na obrázku).
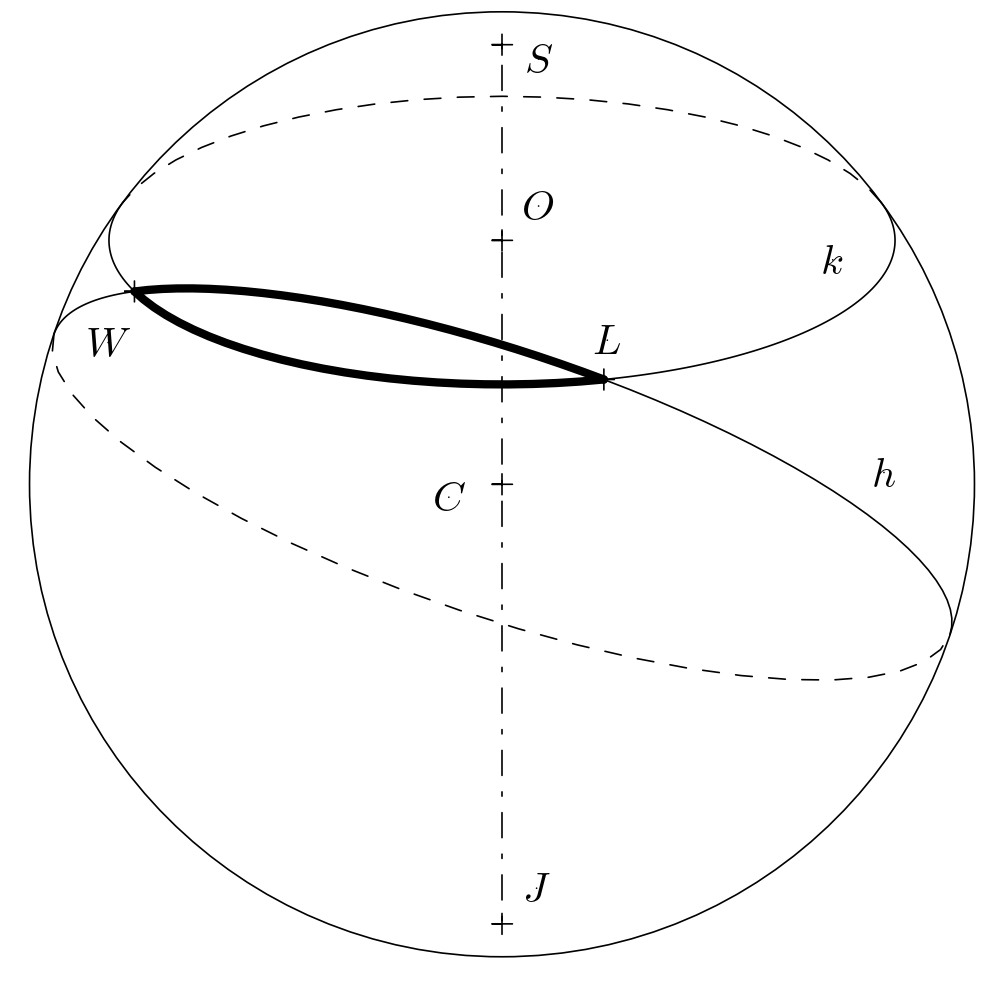
Avšak na guľovom povrchu (ktorý v tejto úlohe budeme považovať za zemský povrch) je najkratšou vzdialenosťou iný oblúk. Tento oblúk je časťou kružnice \(h\), ktorej stred \(C\) je stredom Zeme. Takéto trasy nazývame orthodrómy a všetky kružnice s touto vlastnosťou označujeme ako hlavné kružnice. Koľko kilometrov ušetríme, ak budeme cestovať po orthodróme? Odpoveď na túto otázku je potrebné vypočítať.
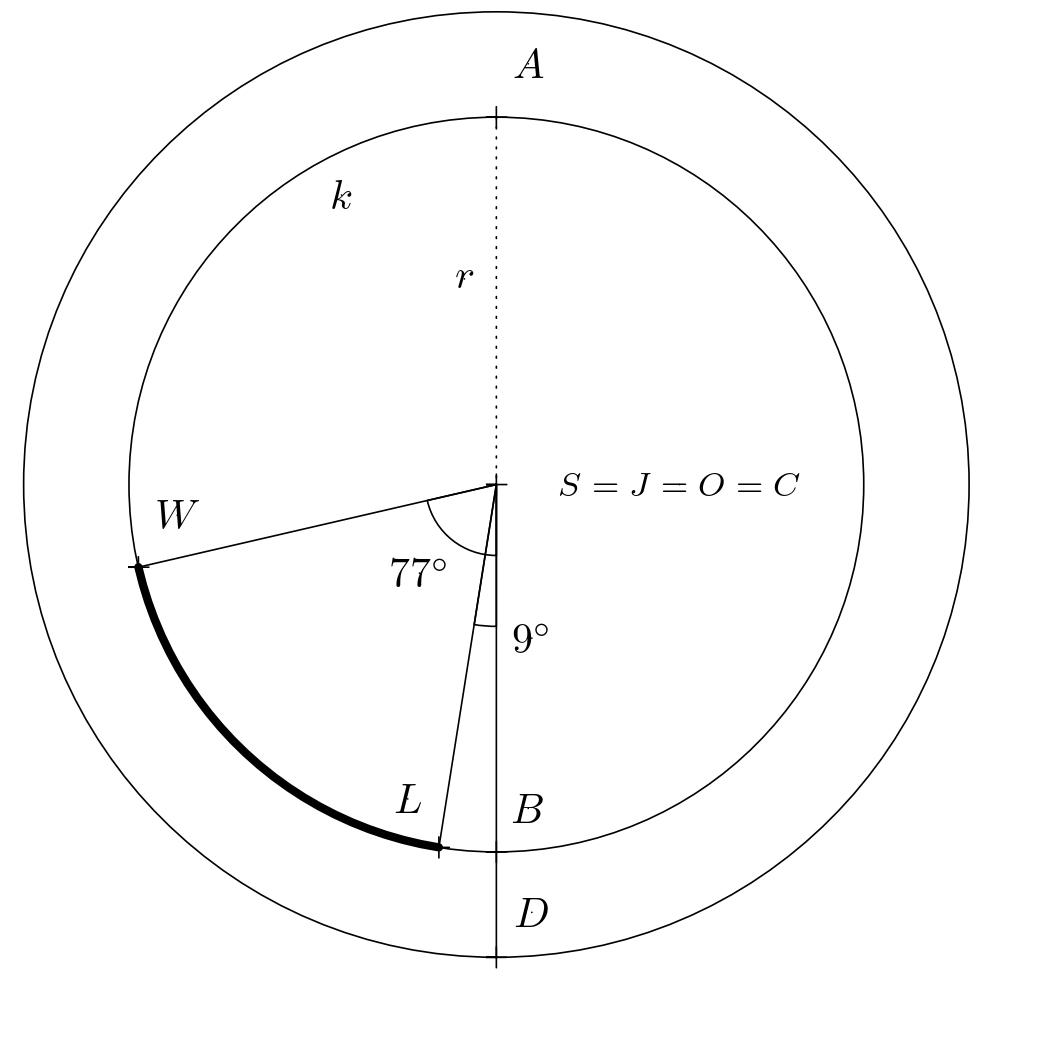
Úloha. Lisabon a Washington sa nachádzajú približne na rovnakej rovnobežke (približne \(39^{\circ}\) severnej zemepisnej šírky). Koľko kilometrov ušetrí lietadlo, ak poletí po orthodrómickej dráhe v porovnaní s letom po rovnobežke? Lisabon sa nachádza približne na \(9^{\circ}\) západnej zemepisnej dĺžky. Washington sa nachádza na \(77^{\circ}\) západnej zemepisnej dĺžky. Predpokladajme, že Zem je guľa so stredom \(C\) a polomerom \(6\ 371\,\text{km}\) a že lietadlo letí v priemernej výške \(10\,\text{km}\) (vzlet a pristátie neuvažujeme). Vo všetkých úvahách teda budeme pracovať s guľou o polomere \(\varrho=6\ 381\,\text{km}\).
Riešenie. Najskôr určíme, koľko kilometrov preletí lietadlo pri ceste po rovnobežke. Označme rovnobežku na \(39^{\circ}\) severnej šírky ako kružnicu \(k\) so stredom \(O\) a polomerom \(r\). Vo vhodnom pravouhlom prieniku zemegule (pozri obrázok, kde \(S\) a \(J\) sú póly) sa uvedená kružnica zobrazí ako úsečka \(AB\) so stredom \(O\).
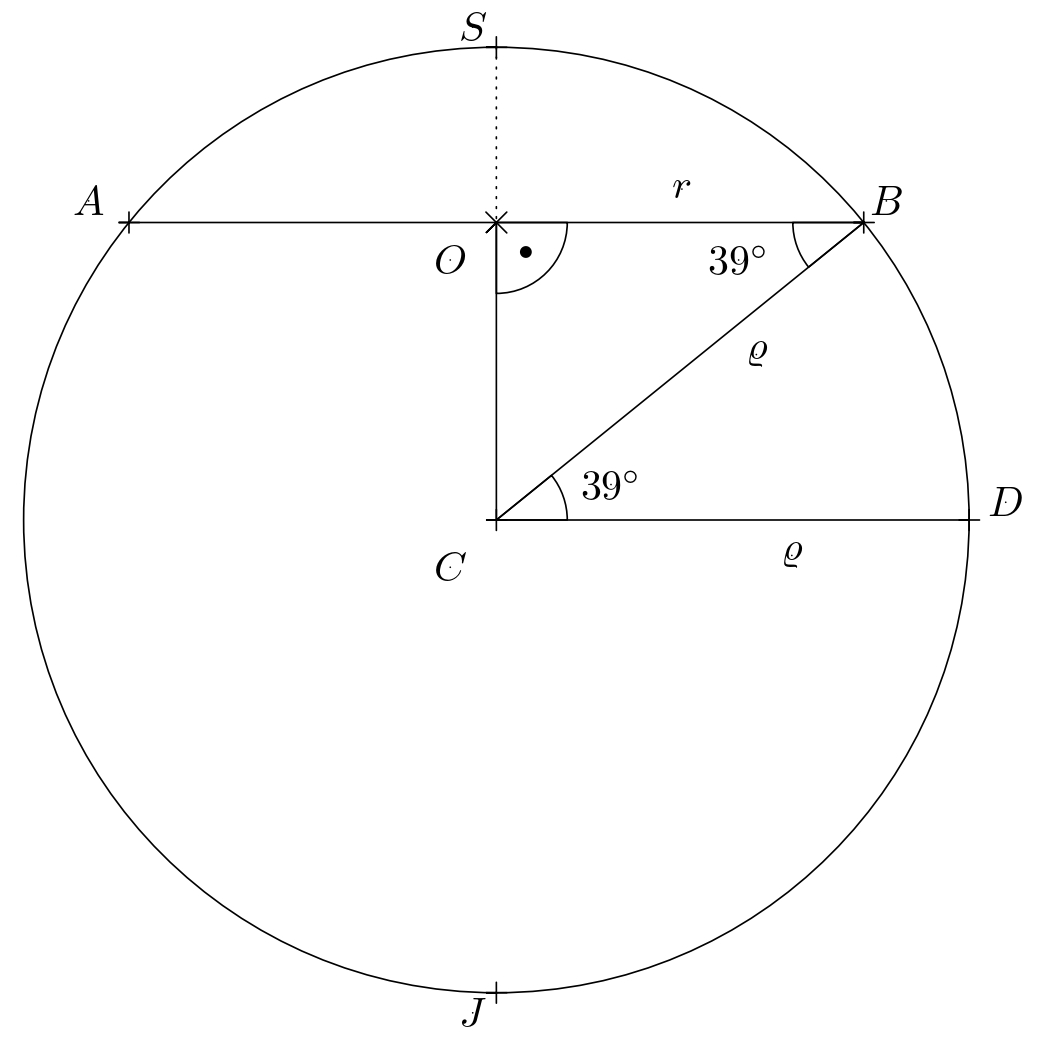
Z obrázku je zrejmá rovnosť \(\lvert\sphericalangle CBO\rvert = \lvert\sphericalangle BCD\rvert\) (uhly sú striedavé) a využitím funkcie kosínus v pravouhlom trojuholníku \(BSO\) dostávame \(r=\varrho\cdot \cos 39^{\circ}\).
Trajektória lietadla pohybujúceho sa po rovnobežke (na obrázku nižšie je trajektória lietadla znázornená kratším oblúkom \(LW\)) sa určí pomocou priamej úmernosti: celá kružnica \(k\) má dĺžku \(2\pi r = 2\pi\varrho\cdot\cos 39^{\circ}\text{km}\), čiže dĺžka kratšieho oblúka \(LW\) sa rovná \[ \frac{(77-9)}{360}\cdot 2\pi\varrho\cdot \cos 39^{\circ} \doteq 5\ 885{,}4\,\text{km}. \]
Teraz určme, koľko kilometrov lietadlo preletí po ortodrome. Ide v podstate o vzdialenosť medzi dvoma bodmi na pomyselnej guli s polomerom \(\varrho=6\ 381\,\text{km}\). Obrázok ukazuje, že ortodroma medzi bodmi \(L\) a \(W\) je istý oblúk hlavnej kružnice \(h\) s neznámym stredovým uhlom \(\varphi\). Potrebujeme určiť veľkosť tohto uhla.
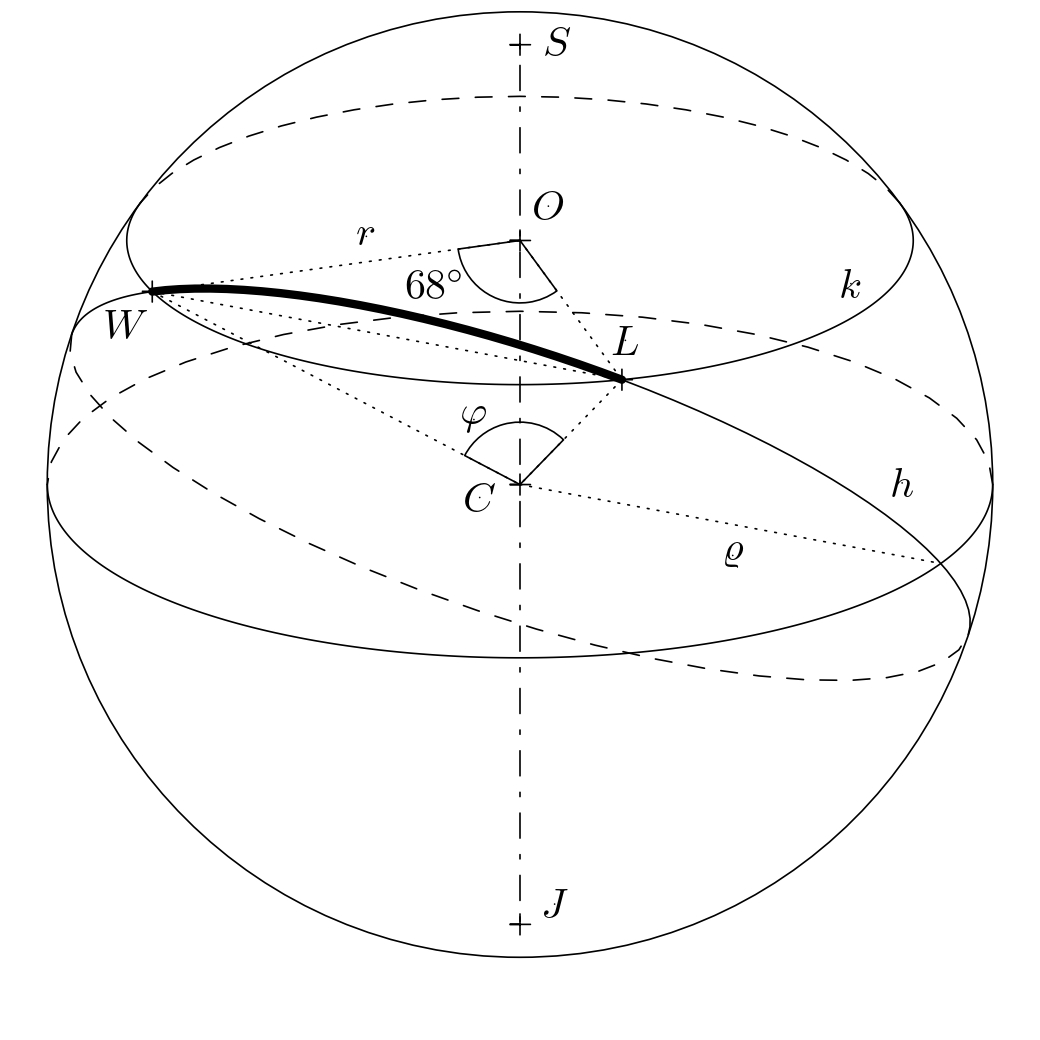
Uvažme rovnoramenný trojuholník \(OWL\), ktorý rozdelíme výškou na základnu \(LW\) na dva zhodné pravouhlé trojuholníky. V ľubovoľnom z týchto dvoch trojuholníkov platí \(\frac{|LW|}{2}=r\cdot \sin 34^{\circ}\), a preto \(|LW|=2r\cdot\sin 34^{\circ}\). Ak budeme uvažovať podobne pre rovnoramenný trojuholník \(CWL\), dostaneme rovnosť \(|LW|=2\varrho \cdot \sin\frac{\varphi}{2}\). Porovnáním pravých strán oboch odvodených rovností vypočítáme hľadaný uhol \(\varphi\):
\[ 2r\sin34^{\circ} = 2\varrho \sin\frac{\varphi}{2} \]
\[ \sin\frac{\varphi}{2} = \frac{r\sin34^{\circ}}{\varrho} = \frac{\varrho \cos39^{\circ}\sin 34^{\circ}}{\varrho} = \cos 39^{\circ}\sin 34^{\circ} \]
\[ \frac{\varphi}{2}= \arcsin \left( \cos 39^{\circ}\sin 34^{\circ} \right) \doteq 25^{\circ}45' \quad \Rightarrow \quad \varphi \doteq 51^{\circ}30'. \]
Dráhu lietadla pohybujúceho sa po ortodrome určujeme podobne ako v prípade rovnobežky, teda priamou úmerou. Dĺžka celej kružnice \(h\) je rovná \(2\pi\varrho\). Pre dĺžku kratšieho oblúka \(LW\) potom platí
\[ \frac{51{,}5}{360}\cdot 2\pi\varrho \doteq 5\ 735{,}5 \,\text{km}. \]
Vidíme, že sa dráhy lišia približne o \(150 \,\text{km}\).
