Nákup vozů pro taxislužbu
 20 min.,
20 min.,  1/3
1/3 V České Republice majitel Pražské taxislužby zvažuje, zda pořídit další vozy a kolik jich pořídit tak, aby jeho zisk byl co největší. Momentálně má 3 vozy a z každého vozu má průměrný měsíční výdělek 60 000 Kč. Dle letitých zkušeností v oboru však očekává, že s každým nakoupeným vozem průměrný výdělek každého vozu klesne o 5 000 Kč, neboť dojde k částečnému přelivu zákazníků do nového vozu. Musí také počítat s tím, že náklady na řidiče a vůz za jeden měsíc činí 40 000 Kč.
Úloha 1. Jaký je měsíční zisk majitele taxislužby nyní?
Řešení. Každý ze tří vozů majiteli taxislužby přináší čistý zisk (po odečtení nákladů) 20 000 Kč. Dohromady tak současný čistý zisk ze tří vozů činí 60 000 Kč.
Úloha 2. Určete funkci, která vyjadřuje zisk majitele taxislužby v závislosti na počtu nově dokoupených vozů. O jakou funkci se jedná a jak vypadá její graf?
Řešení. Označme \(x\) počet nově pořízených vozů a \(y\) zisk majitele za jeden měsíc. Víme, že čistý zisk jednoho ze stávajících tří vozů je 20 000 Kč. Od této částky je třeba odečíst částku snížení tržby z jednoho vozu při dokoupení \(x\) vozů. Celkem tedy jeden vůz přinese majiteli zisk \(20\ 000-5\ 000x\) Kč. Celkový zisk při dokoupení \(x\) vozů dostaneme vynásobením tohoto výrazu novým počtem aut:
\[ y=(20\ 000-5\ 000x)(x+3) \]
Po roznásobení a úpravě pravé strany jde vidět, že funkce \[f\colon y= -5\ 000x^2 + 5\ 000x + 60\ 000\] je kvadratická. Jejím grafem je konkávní parabola, protože koeficient u kvadratického členu je záporný.
Úloha 3 Určete jaký je maximální možný zisk majitele. O kolik se tento zisk liší od současného? Kolik vozů musí majitel koupit (nebo eventuálně prodat)?
Řešení. Naším úkolem je nyní určit maximum funkce \(f\). To se nachází v bodě, který je aritmetickým průměrem reálných kořenů kvadratického polynomu (za předpokladu, že existují). Tyto kořeny nyní určíme:
\[ \begin{aligned} -5\ 000x^2 + 5\ 000x + 60\ 000 &= 0 \\ x^2 - x - 12 &= 0\\ (x-4)(x+3)&=0 \end{aligned} \]
Kořeny kvadratické rovnice jsou \(x_1=4\) a \(x_2=-3\), tedy maximum funkce \(f\) je v bodě \[x_{max}=\frac{-3+4}{2}=\frac{1}{2}.\]
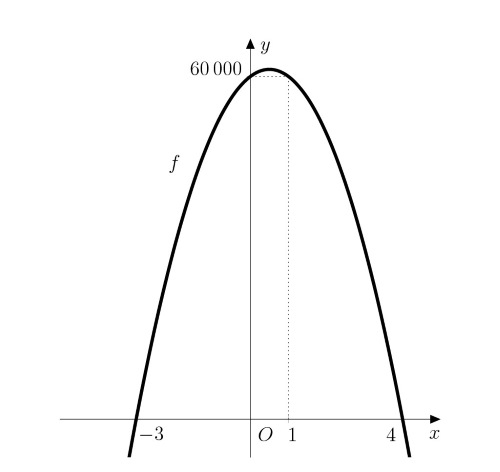
Toto maximum je však nedosažitelné (nelze koupit půl auta). Nejvyšší funkční hodnota, kterou má smysl uvažovat, se v tomto případě nachází v nejbližších celočíselných bodech, tj. \(x=0\) nebo \(x=1\) (v obou bodech je stejná, jak plyne ze symetrie paraboly). To však znamená, že pro majitele není výhodné pořizovat další auta, protože jeho aktuální zisk je rovněž maximálním.