Čepice na karneval
 15 min.,
15 min.,  1/3
1/3 Osmiletá Anička chce jít na dětský karneval v kostýmu bílé paní, jehož součástí bude i bílá čepice kuželovitého tvaru. Rodiče využili příležitosti procvičit si s Aničkou geometrickou představivost a místo nákupu se rozhodli s ní čepici vyrobit.
Úloha 1. Anička s maminkou zjistili krejčovským metrem, že obvod Aniččiny hlavy je 52 cm. Společně se dále dohodli, že čepice bude 30 cm vysoká. Jak čepici vyrobí?
Řešení. Čepice je tvořena pláštěm kužele, kde známe obvod podstavy \(o\) (52 cm) a výšku kužele \(v\) (30 cm). Rozbalený plášť kužele je pak kruhovou výsečí o neznámém poloměru \(s\) (velikost strany kužele) a neznámém středovém úhlu \(\varphi\). Tyto údaje musíme vypočítat. Dále víme, že délka oblouku kruhové výseče je rovna obvodu \(o\).
Nejprve z obvodu podstavy spočítáme poloměr podstavy \(r\) a poté Pythagorovou větou délku strany \(s\).
\[ r = \frac{o}{2\pi} = \frac{52}{2\pi} \doteq 8{,}28\,\text{cm} \]
\[ s = \sqrt{v^2 + r^2} = \sqrt{30^2 + 8{,}28^2} \doteq 31{,}12\,\text{cm} \]
Nyní určíme úhel \(\varphi\). Vypočítáme nejprve obvod \(O\) celého kruhu o poloměru \(s\), dostáváme
\[ O = 2\pi s \doteq 195{,}53 \,\text{cm}. \]
Následně využijeme přímé úměrnosti mezi délkou oblouku tohoto kruhu a příslušným středovým úhlem k výpočtu úhlu \(\varphi\):
\[ \varphi = \frac{o}{O}\cdot 360^{\circ} = \frac{52}{195{,}53}\cdot 360^{\circ} \doteq 95^{\circ}44'. \]
Čepici Anička s rodiči vyrobí z kruhové výseče o přibližném poloměru 31 cm a středovém úhlu přibližně \(96^{\circ}\).
Úloha 2. Na konci karnevalu se konaly soutěže a Anička hned v první soutěži vyhrála sáček bonbónů. Čepici kuželovitého tvaru použila jako kornout a bonbóny do něj přesypala. Bonbóny zaplnily kornout do poloviny jeho výšky. Kolik sáčků bonbónů (stejného druhu) musí ještě vyhrát, aby kornout naplnila až po okraj?
Řešení. Úlohu budeme řešit obecně (lze ji ale řešit i s konkrétními rozměry z první úlohy). Víme že objem kornoutu tvaru kuželu spočítáme podle vzorce \(V=\frac{1}{3}\pi r^2v\).
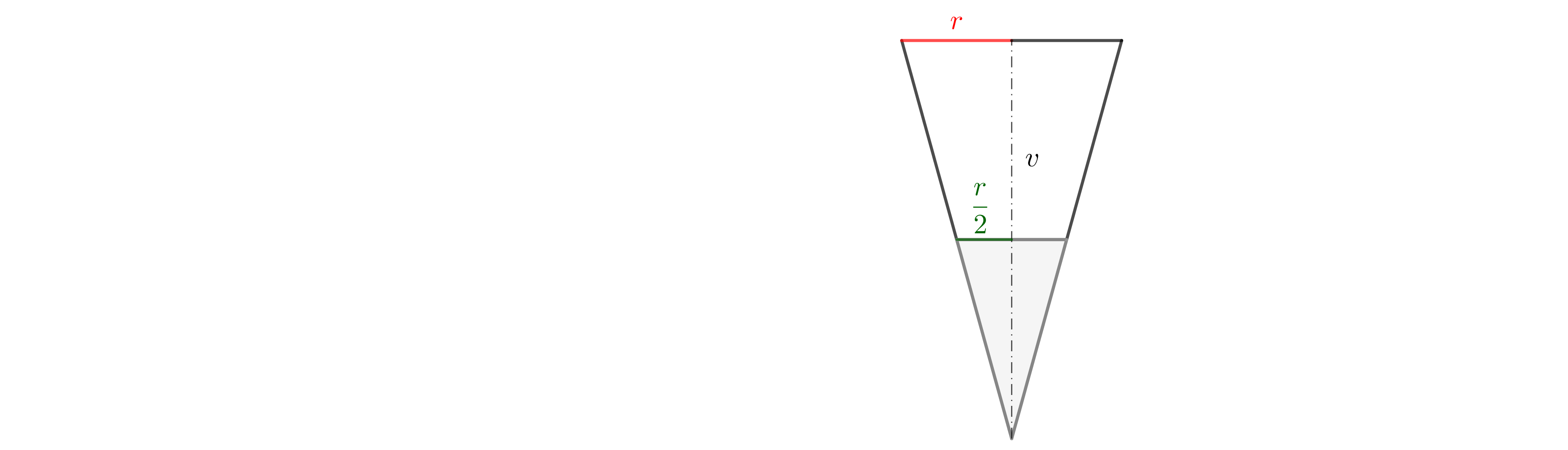
Kužel, který je naplněn bonbóny (na obrázku vyznačený šedě) má poloviční výšku a tedy i poloviční poloměr (plyne z podobnosti trojúhelníků) a jeho objem spočítáme jako
\[V'=\frac{1}{3}\pi \left(\frac{r}{2}^2\right)\frac{v}{2}=\frac{1}{3}\pi\frac{r^2}{4}\frac{v}{2}=\frac{1}{24}\pi r^2v=\frac{1}{8}V.\]
Objem zbývajícího volného prostoru v kornoutu je pak \(V-V'=\frac{7}{8}V\). Zbývá tedy určit kolikrát se do tohoto volného prostoru vejde \(V'\), tedy
\[\frac{V-V'}{V'}= \frac{\frac{7}{8}V}{\frac{1}{8}V}=7.\]
Anička musí vyhrát ještě 7 sáčků bonbónů, aby kornout naplnila až po okraj.