Majiteľ pražskej taxislužby v Českej republike zvažuje, či má kúpiť ďalšie vozidlá a koľko ich kúpiť, aby maximalizoval svoj zisk. V súčasnosti má 3 autá, z ktorých každé mu prináša priemerný mesačný príjem 60 000 Kč. Na základe dlhoročných skúseností v tomto odvetví však očakáva, že s každým ďalším kúpeným autom sa priemerný príjem na jedno auto zníži o 5 000 Kč v dôsledku čiastočného presunu zákazníkov na nové auto. Musí tiež vziať do úvahy, že náklady na vodiča a auto predstavujú 40 000 Kč mesačne.
Úloha 1. Aký je v súčasnosti mesačný zisk majiteľa taxislužby?
Riešenie. Každé z troch áut prináša majiteľovi taxislužby čistý zisk (po odpočítaní nákladov) 20 000 Kč. Celkový súčasný čistý zisk z troch áut je teda 60 000 Kč.
Úloha 2. Určte funkciu, ktorá vyjadruje zisk majiteľa taxislužby v závislosti na počte novo zakúpených vozidiel. Aká je to funkcia a ako vyzerá jej graf?
Riešenie. Označme \(x\) počet nových vozidiel a \(y\) zisk majiteľa za jeden mesiac. Vieme, že čistý zisk jedného z troch existujúcich áut je 20 000 Kč. Od tejto sumy musíme odpočítať čiastku, ktorá predstavuje zníženie tržieb z jedného auta pri nákupe \(x\) áut. Celkovo teda jedno auto prinesie majiteľovi zisk vo výške \(20\ 000-5\ 000x\) Kč. Celkový zisk pri nákupe \(x\) áut získame vynásobením tohto výrazu novým počtom áut:
\[ y=(20\ 000-5\ 000x)(x+3) \]
Po vynásobení a úprave pravej strany vidíme, že funkcia \[f\colon y= -5\ 000x^2 + 5\ 000x + 60\ 000,\] je kvadratická. Jej graf je konkávna parabola, pretože koeficient kvadratického člena je záporný.
Úloha 3 Určte aký je maximálny možný zisk majiteľa. O koľko sa tento zisk líši od súčasného zisku? Koľko áut musí majiteľ kúpiť (prípadne predať)?
Riešenie. Našou úlohou je teraz určiť maximum funkcie \(f\). To sa nachádza v bode, ktorý je aritmetickým priemerom reálnych koreňov kvadratického polynómu (za predpokladu, že existujú). Tieto korene teraz určíme:
\[ \begin{aligned} -5\ 000x^2 + 5\ 000x + 60\ 000 &= 0 \\ x^2 - x - 12 &= 0\\ (x-4)(x+3)&=0 \end{aligned} \]
Korene kvadratickej rovnice sú \(x_1=4\) a \(x_2=-3\), teda maximum funkcie \(f\) je v bode \[x_{max}=\frac{-3+4}{2}=\frac{1}{2}.\]
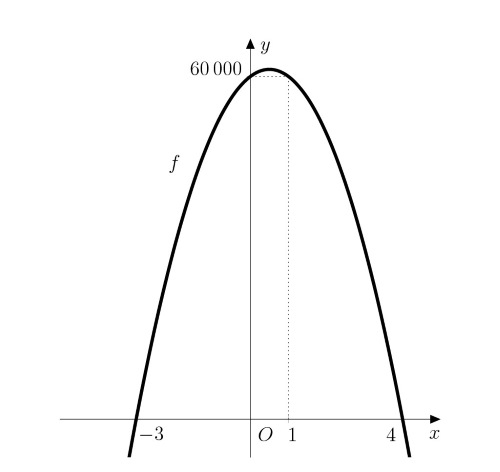
Toto maximum je však nedosiahnuteľné (nie je možné kúpiť polovicu auta). Najvyššia funkčná hodnota, ktorú má zmysel v tomto prípade uvažovať, sa nachádza v najbližších celočíselných bodoch, t. j. \(x=0\) alebo \(x=1\) (oba body dávajú rovnakú hodnotu vzhľadom na symetriu paraboly). To však znamená, že pre majiteľa nie je výhodné kupovať ďalšie autá, pretože jeho súčasný zisk je zároveň maximálnym možným ziskom.