Optimización de la compra de coches para el servicio de taxi
 20 min.,
20 min.,  1/3
1/3 En la República Checa, el propietario del servicio de taxis de Praga se plantea si comprar más coches y cuántos comprar para maximizar sus beneficios. Actualmente tiene 3 coches, cada uno de los cuales le reporta unos ingresos medios mensuales de 60 000 CZK. Sin embargo, basándose en años de experiencia en el sector, prevé que, con cada coche más, los ingresos medios por coche disminuirán en 5 000 CZK debido al cambio parcial de clientes al nuevo coche. También debe tener en cuenta que los costes de un conductor y un coche ascienden a 40 000 CZK al mes.
Ejercicio 1. ¿Cuál es actualmente el beneficio mensual del propietario del servicio de taxi?
Solución. Cada uno de los tres coches reporta al propietario del servicio de taxi un beneficio neto (una vez deducidos los costes) de 20 000 CZK. Por lo tanto, el beneficio neto actual total de los tres coches es de 60 000 CZK.
Ejercicio 2. Determina la función que expresa el beneficio del propietario del servicio de taxi en función del número de coches comprados. ¿Qué tipo de función es y qué aspecto tiene su gráfica?
Solución. Sea \(x\) el número de coches comprados y \(y\) el beneficio mensual del propietario. Sabemos que el beneficio neto de uno de los tres coches existentes es de 20 000 CZK. A esta cantidad le restamos la disminución de los ingresos de un coche cuando se compran \(x\) coches adicionales. Así, en total, un coche reportaría al propietario un beneficio de 20.000-5.000x$ CZK. Obtenemos el beneficio total multiplicando esta expresión por el nuevo número de coches:
\[ y=(20\ 000-5\ 000x)(x+3) \]
Expandiendo y simplificando la expresión, obtenemos la función \[f\colon y= -5\ 000x^2 + 5\ 000x + 60\ 000,\] que es cuadrática. Su gráfica es una parábola cóncava porque el coeficiente del término cuadrático es negativo.
Ejercicio 3. Determina el beneficio máximo posible del propietario. ¿En cuánto difiere este beneficio del beneficio actual? ¿Cuántos coches tiene que comprar (o posiblemente vender) el propietario?
Solución. Nuestra tarea ahora es determinar el máximo de la función \(f\). Éste se encuentra en el punto que es la media aritmética de las raíces reales de un polinomio cuadrático (suponiendo que existan). Ahora determinaremos estas raíces:
\[ \begin{aligned} -5\ 000x^2 + 5\ 000x + 60\ 000 &= 0 \\ x^2 - x - 12 &= 0\\ (x-4)(x+3)&=0 \end{aligned} \]
Las raíces del polinomio cuadrático son \(x_1=4\) y \(x_2=-3\). Por tanto, el máximo de la función \(f\) está en el punto \[x_{max}=\frac{-3+4}{2}=\frac{1}{2}.\]
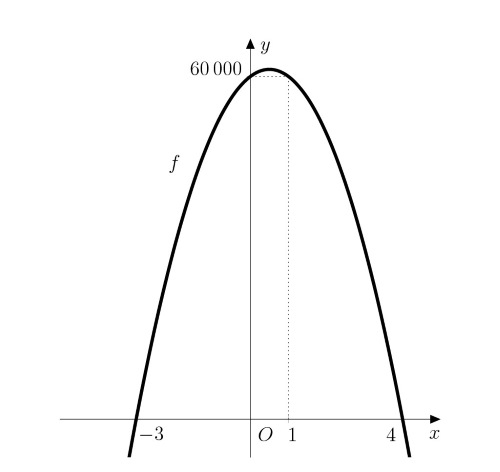
Sin embargo, este máximo es inalcanzable (no es posible comprar medio coche). El valor funcional más alto que tiene sentido considerar en este caso se sitúa en los puntos enteros más cercanos, es decir, \(x=0\) o \(x=1\) (ambos puntos dan el mismo valor debido a la simetría de la parábola). Sin embargo, esto significa que no es ventajoso para el propietario comprar más coches porque su beneficio actual es también el máximo posible.