Optymalizacja zakupu samochodu dla usług taksówkarskich
 20 min.,
20 min.,  1/3
1/3 W Czechach właściciel praskich usług taksówkarskich rozważa, czy kupić dodatkowe samochody i ile ich kupić aby zmaksymalizować swój zysk. Obecnie posiada 3 samochody, z których każdy przynosi średni miesięczny dochód w wysokości 60 000 CZK. Jednak w oparciu o wieloletnie doświadczenie w branży, spodziewa się, że z każdym dodatkowym zakupionym samochodem średni dochód na samochód zmniejszy się o 5 000 CZK z powodu częściowego przejścia klientów na nowy samochód. Musi również wziąć pod uwagę, że koszty kierowcy i samochodu wynoszą 40 000 CZK miesięcznie.
Zadanie 1. Jaki jest obecnie miesięczny zysk właściciela taksówki?
Rozwiązanie. Każdy z trzech samochodów przynosi właścicielowi taksówki zysk netto (po odjęciu kosztów) w wysokości 20 000 CZK. Zatem całkowity bieżący zysk netto z trzech samochodów wynosi 60 000 CZK.
Zadanie 2. Wyznacz funkcję wyrażającą zysk właściciela taksówki jako funkcję liczby przejechanych taksówek. nowo zakupionych samochodów. Jakiego typu jest to funkcja i jak wygląda jej wykres?
Rozwiązanie. Niech \(x\) oznacza liczbę nowo zakupionych samochodów, a \(y\) oznacza miesięczny zysk właściciela. Wiemy, że zysk netto jednego z trzech istniejących samochodów wynosi 20 000 CZK. Od tej kwoty odejmujemy spadek przychodów z jednego samochodu, gdy dodatkowo zakupionych zostanie \(x\) samochodów. Tak więc, w sumie, jeden samochód przyniósłby zysk w wysokości \(20\ 000-5\ 000x\) CZK dla właściciela. Całkowity zysk otrzymujemy mnożąc przez nową liczbę samochodów:
\[ y=(20\ 000-5\ 000x)(x+3) \]
Rozszerzając i upraszczając wyrażenie, otrzymujemy funkcję \[f\colon y= -5\ 000x^2 + 5\ 000x + 60\ 000,\] która jest kwadratowa. Jej wykres jest wklęsłą parabolą, ponieważ współczynnik wyrażenia kwadratowego jest ujemny.
Zadanie 3. Określ maksymalny możliwy zysk właściciela. Jak bardzo ten zysk różni się od obecnego zysku? Ile samochodów właściciel musi kupić (lub ewentualnie sprzedać)?
Rozwiązanie. Naszym zadaniem jest teraz wyznaczenie maksimum funkcji \(f\). Znajdziemy je w punkcie, który jest średnia arytmetyczna rzeczywistych pierwiastków wielomianu kwadratowego (przy założeniu, że że istnieją). Określimy teraz te pierwiastki:
\[ \begin{aligned} -5\ 000x^2 + 5\ 000x + 60\ 000 &= 0 \\ x^2 - x - 12 &= 0\\ (x-4)(x+3)&=0 \end{aligned} \]
Pierwiastkami wielomianu kwadratowego są \(x_1=4\) i \(x_2=-3\). Zatem maksimum funkcji \(f\) wynosi w punkcie \[x_{max}=\frac{-3+4}{2}=\frac{1}{2}.\]. 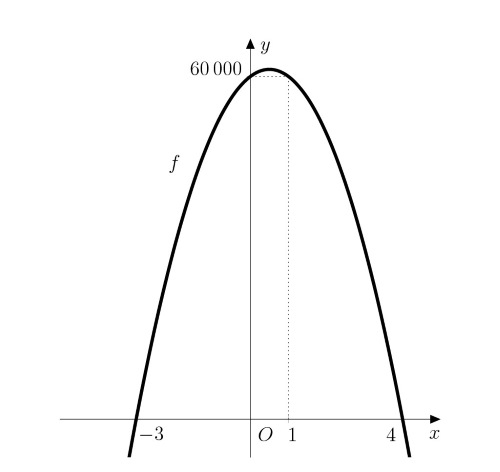
Jednak to maksimum jest nieosiągalne (nie jest możliwe, aby kupić pół samochodu). Najwyższa wartość funkcjonalna, którą warto rozważyć w tym przypadku, znajduje się w najbliższych punktach całkowitych, tj. \(x=0\) lub \(x=1\) (oba punkty dają tę samą wartość ze względu na symetrię paraboli). Oznacza to jednak, że że nie jest korzystne dla właściciela kupowanie dodatkowych samochodów, ponieważ jego obecny zysk jest również maksymalnym możliwym zyskiem.