In the Czech Republic, the owner of Prague’s taxi service is considering whether to buy additional cars and how many to buy in order to maximize his profit. Currently, he has 3 cars, each earning an average monthly income of 60 000 CZK. However, based on years of experience in the industry, he expects that with each additional car purchased, the average income per car will decrease by 5 000 CZK due to a partial shift of customers to the new car. He also needs to consider that the costs for a driver and a car amount to 40 000 CZK per month.
Exercise 1. What is the monthly profit of the taxi service owner currently?
Solution. Each of the three cars earns to the taxi service owner a net profit (after deducting costs) of 20 000 CZK. Therefore, the total current net profit from the three cars is 60 000 CZK.
Exercise 2. Determine the function that expresses the profit of the taxi service owner as a function of the number of newly purchased cars. What type of function is it, and what does its graph look like?
Solution. Let \(x\) denote the number of newly purchased cars, and \(y\) denote the owner’s profit per month. We know that the net profit of one of the existing three cars is 20 000 CZK. From this amount, we subtract the decrees in revenue from one car when \(x\) cars are purchased additionally. So, in total, one car would bring a profit of \(20\ 000-5\ 000x\) CZK to the owner. We obtain the total profit by multiplying this expression by the new number of cars:
\[ y=(20\ 000-5\ 000x)(x+3) \]
By expanding and simplifying the expression, we get the function \[f\colon y= -5\ 000x^2 + 5\ 000x + 60\ 000,\] which is quadratic. Its graph is a concave parabola because the coefficient of the quadratic term is negative.
Exercise 3. Determine the owner’s maximum possible profit. How much does this profit differ from the current profit? How many cars does the owner have to buy (or possibly sell)?
Solution. Our task now is to determine the maximum of the function \(f\). This is found at the point that is
the arithmetic mean of the real roots of a quadratic polynomial (assuming that they exist). We will determine these roots now:
\[ \begin{aligned} -5\ 000x^2 + 5\ 000x + 60\ 000 &= 0 \\ x^2 - x - 12 &= 0\\ (x-4)(x+3)&=0 \end{aligned} \]
The roots of the quadratic polynomial are \(x_1=4\) and \(x_2=-3\). Therefore, the maximum of the function \(f\) is at the point \[x_{max}=\frac{-3+4}{2}=\frac{1}{2}.\]
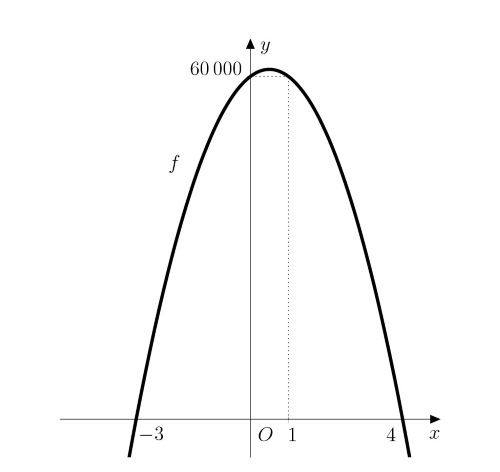
However, this maximum is unattainable (it is not possible to buy half a car). The highest functional value that makes sense to consider in this case is located at the nearest integer points, i.e., \(x=0\) or \(x=1\) (both points yield the same value due to the symmetry of the parabola). However, this means that it is not advantageous for the owner to buy additional cars because his current profit is also the maximum possible profit.