Anamorphosis is a type of visual trick or art in which a portion of a plane or space seen from a particular angle reveals a hidden image. Anamorphosis depends on the observer finding the right place from which to look. This kind of art has a long and rich history. One of the most famous paintings using anamorphosis is The Ambassadors (1533) by the German painter Hans Holbein the Younger (1497 - 1543).
A certain strange elongated object is painted at the bottom of the painting. You can only make out what it is if you stand against the wall near the right frame of the painting and look in that direction. If you find the right position from which to look, you will see that it is a skull.
Anamorphic art can also use reflections of paintings or sculptures in a cylinder1.
Towards the end of the 20th century, anamorphic art experienced a great revival in photography, drawing and large-scale installations. Some artists create anamorphic images from everyday objects such as electronics, shoes and socks2. Anamorphoses can also be encountered within street art. Often these are drawings on the pavement, road or wall that surprise and momentarily confuse the casual passer-by. For example, it can be a drawing that looks like a hole in the ground, into which a fall is imminent, legs sticking out of a wall or a canal, etc. Anamorphoses based on central projection are more convincing when viewed with one eye or through a lens. But if the center of the projection is far enough away from the object being observed, is well shaded, or its surroundings somehow support the impression of space, the illusion is more convincing.
The film industry sometimes uses cameras with anamorphic lenses to shoot movies. They were originally designed so that wide-format images would fully utilize the area of standard 35mm film frames. Otherwise, wide-format images would leave the top and bottom of the frame unused. Despite the advent of high-resolution digital sensors, anamorphic lenses are still used today for the uniqueness of the resulting image.
Some cities introduced pedestrian crossings that at some point looked like levitating prisms from the perspective of oncoming drivers. After a short trial period, they were usually canceled because drivers braked too hard in front of them.
The anamorphic projection technique can be seen in some sports stadiums, where it is used to promote company logos that are painted on the playing field. From the angle of the television camera, the inscription appears as inscriptions standing vertically within the playing field.
In the following text and examples, we will create anamorphoses of basic solids using central projection onto a plane. The plane in which we will draw these anamorphic images will be called the projection plane. The projection plane for us will be the paper on which we will draw. This will limit us in terms of the size of the objects. We will then observe the resulting images through the camera eye via a mobile phone or camera. If you have the opportunity, you can create anamorphic images outdoors, ideally away from traffic.
It is probably easiest to create anamorphic images of a pyramid and a cone, provided that their bases lie in the projection planes. Let’s explain the principle on a pyramid. In addition to the solid, it is necessary to enter the projection center \(S\) and its perpendicular projection onto the projection plane \(S_1\). We can imagine the projection center as the observer’s eye. The perpendicular projection as the place where the observer stands. The distance \(S _1S = d\) is therefore the distance of the projection center from the projection plane. For a regular tetrahedral pyramid, we similarly denote its vertex as \(V\) and the perpendicular projection of the vertex onto the projection plane as \(V_1\). The intersection of the line \(SV\) (the so-called projection ray) with the projection plane is then obtained as the intersection of the line \(SV\) with the line \(S_1V_1\) (see the following figure on the left). It is a good idea to sketch such a picture when we are thinking about how the illusion works and what the central projection will look like. However, this spatial picture is not needed to determine the anamorphosis of the pyramid.
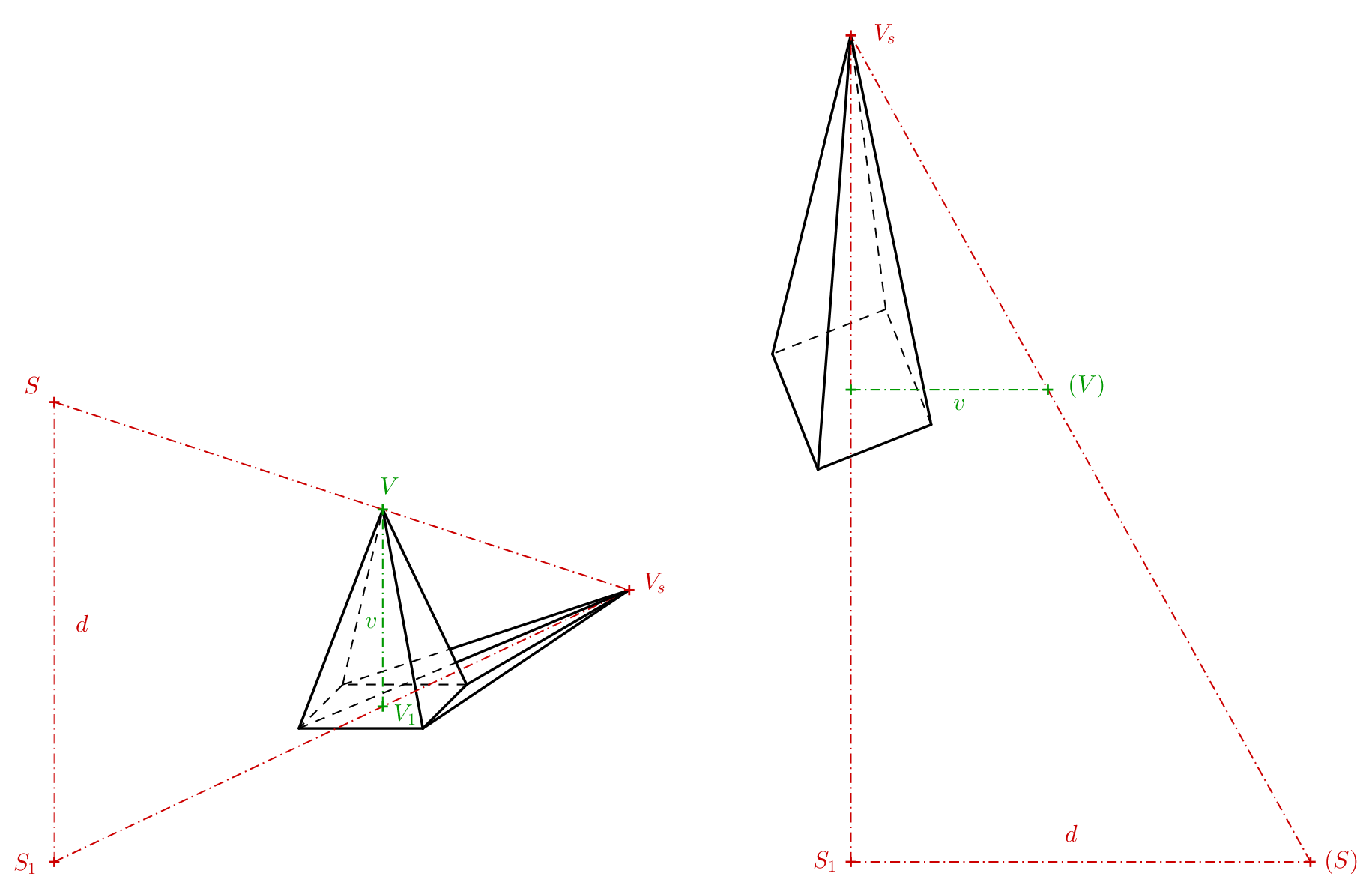
The only thing that is important to us is the trapezoid \(S_1V_1VS\), which we can also represent in the projection as the trapezoid \(S_1V_1(V)(S)\) (previous image on the right). The points that were previously in space outside the projection (points \(V\) and \(S\)) are now shown in parentheses in the projection to distinguish them from each other. The points \((V)\) and \((S)\) were created by rotating the plane \(S_1VS\) by \(90^\circ\) into the projection around the line \(S_1V_1\). If we know the height of the pyramid, the distance of the observer’s eye from the projection, and the distance \(S_1V_1\), then we can draw the trapezoid. By extending its sides that are not parallel to each other, we get the intersection point \(V_s\).
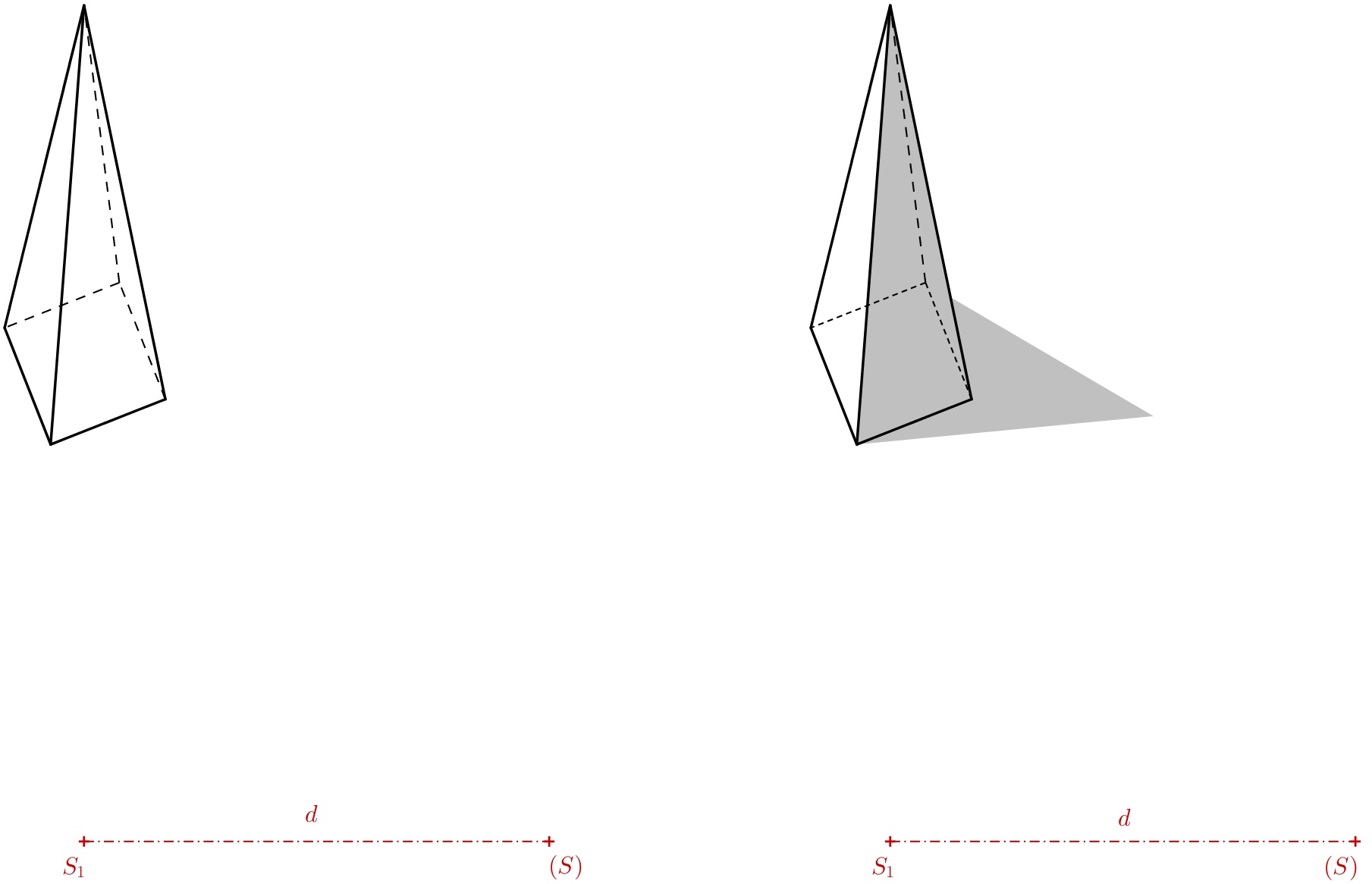
The result (see the previous image on the left) is best drawn without auxiliary lines. We can look at it through the camera’s eye. When looking through the camera’s eye, we find that the invisible edges of the lower base are best drawn with a denser dashed line than the projection of the invisible side edge. If we want the pyramid to look believable, we shade the image. We can only estimate the shadow, we can choose the shadow cast by the top. The anamorphosis of the pyramid is complete, the camera’s camera (for the illusion to work) needs to be set above the point \(S_1\) at a height equal to the distance \(S_1(S)\). The resulting image through the camera’s eye should look approximately like the following image.
Exercise 1. We want to draw a shape on the ground that will look like a cone with a height of \(1\,\mathrm{m}\) and a base with a radius of \(r=0{,}4\,\mathrm{m}\) in space. We will again denote the center of projection by \(S\) and its perpendicular projection by \(S_1\). We assume that the eye of an average observer is at a height of \(150\,\mathrm{cm}\) from the ground. At what distance must \(V_s\) be from \(V_1\) (\(V_s\) is the central projection of the cone’s vertex onto the projection plane, \(V_1\) is the perpendicular projection of the cone’s vertex onto the projection plane)?
Solution. Triangles \(S_1V_sS\) and \(V_1V_sV\) are similar.
Therefore, the ratios of the corresponding sides are equal:
\[\frac{x}{1}= \frac{x+3}{1{,}5},\]
\[1{,}5\,x=x+3,\]
from which we get \(x=6\). The distance of the point \(V_s\) from \(V_1\) must be \(6\) meters.
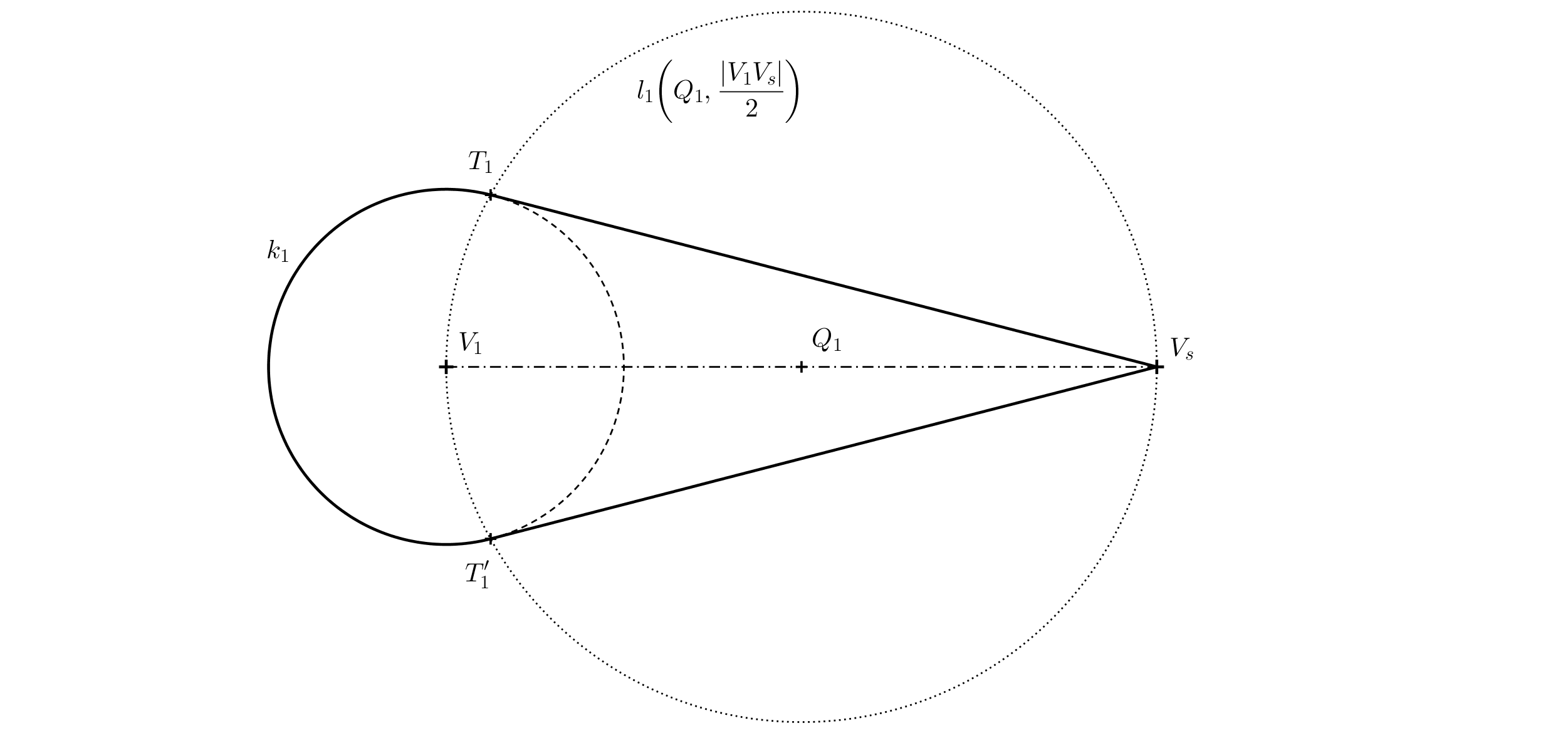
Exercise 2. We have a given base circle \(k\) with center \(V_1\) and point \(V_s\) (see figure for the assignment). Now imagine a cone of revolution in space with base circle \(k\) and projection center \(S\), such that \(V_s\) is the central projection of the cone’s vertex. \(V_1\) is the perpendicular projection of the cone’s vertex onto the projection plane (on paper). Determine the contour of the central projection of the cone.
Solution. The contour of the cone will (except for part of the base circle) be formed by tangents from the vertex \(V_s\). More precisely, these will be the lines connecting the point \(V_s\) with the points of contact \(T\) and \(T'\), which we obtain as the intersections of the Thales circle \(l\) over the diameter \(V_1V_s\) with the circle \(k\).
Exercise 3. For the solution of the previous exercise, determine the position of the center of \(S\) (using \(S_1\) and \((S)\)), if we know the height \(v\) of the solid cone and \(d=\left|S_1S\right|\). See the following figure for the assignment, the lengths of \(v\) and \(d\) are given by the segments.
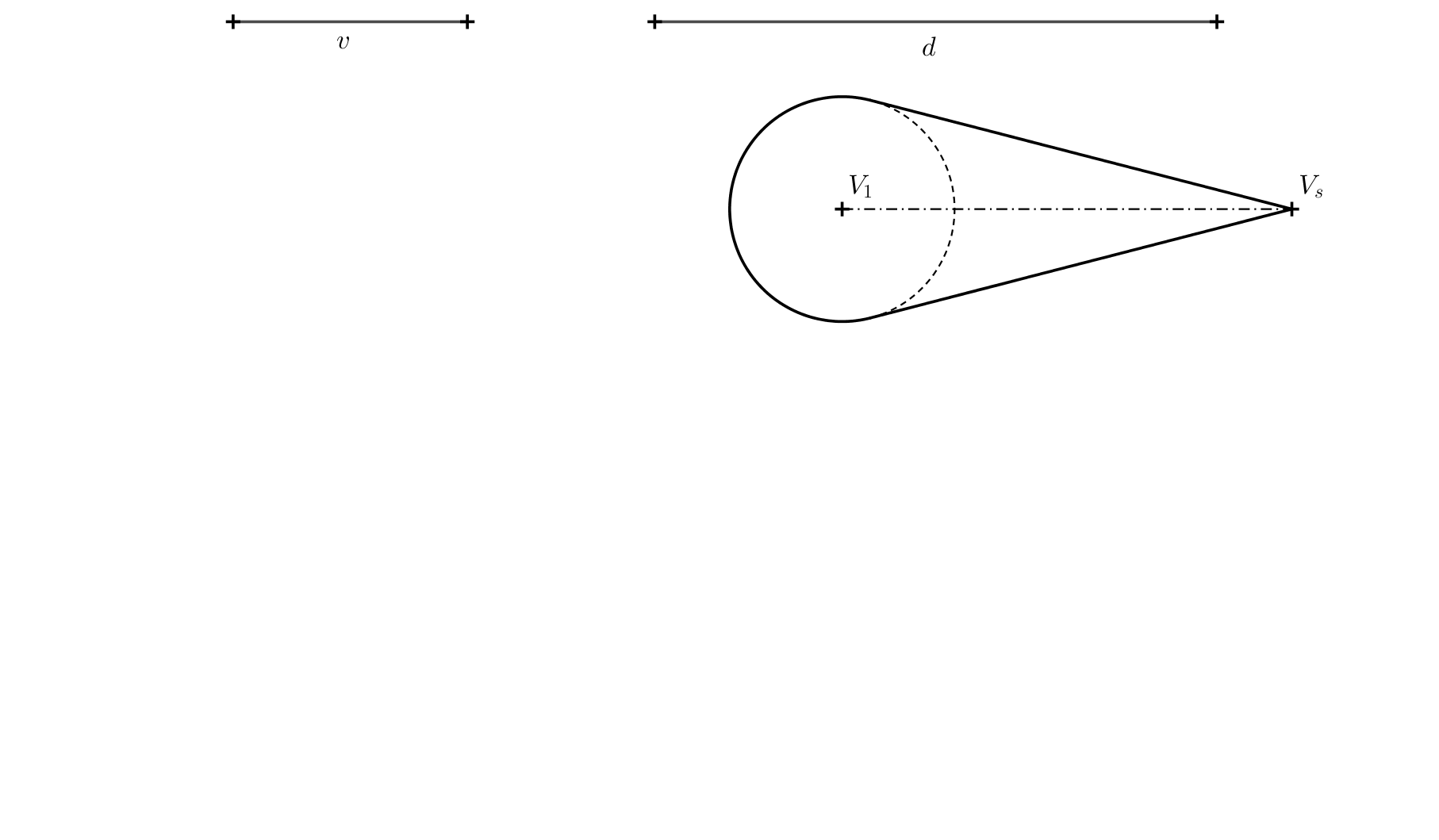
Solution.Point \(S\) must meet two conditions. Its distance from the projection is equal to \(d\) and it must lie on the line \(VV_s\). The center of \(S\) and point \(V\) lie in a plane perpendicular to the projection. The intersection of these two planes is the line \(o=V_1V_s\). We can rotate the vertex \(V\) around this line by \(90^\circ\) to the projection. We denote the rotated image of point \(V\) by \((V)\), it must lie at a distance \(v\) from point \(V_1\) on the perpendicular to the axis \(o\). At a distance \(d\) from the axis \(o=V_1V_s\) we draw a line \(p\). Point \((S)\) must lie at the intersection of the lines \(p\) and \((V)V_s\)
When anamorphically displaying a prism and a cylinder, we will use homothetic transformation. We will explain why this is the case using the example of a cube in the following figure. Between the upper base of the cube and its projection, there is an homothetic relation in space with the center \(S\) (it follows from the similarity of triangles). Since the lower base of the cube is also the perpendicular projection of the upper base onto the projection plane, then the homothetic transformation with the center \(S_1\) between the lower base and the central projection of the upper base works.
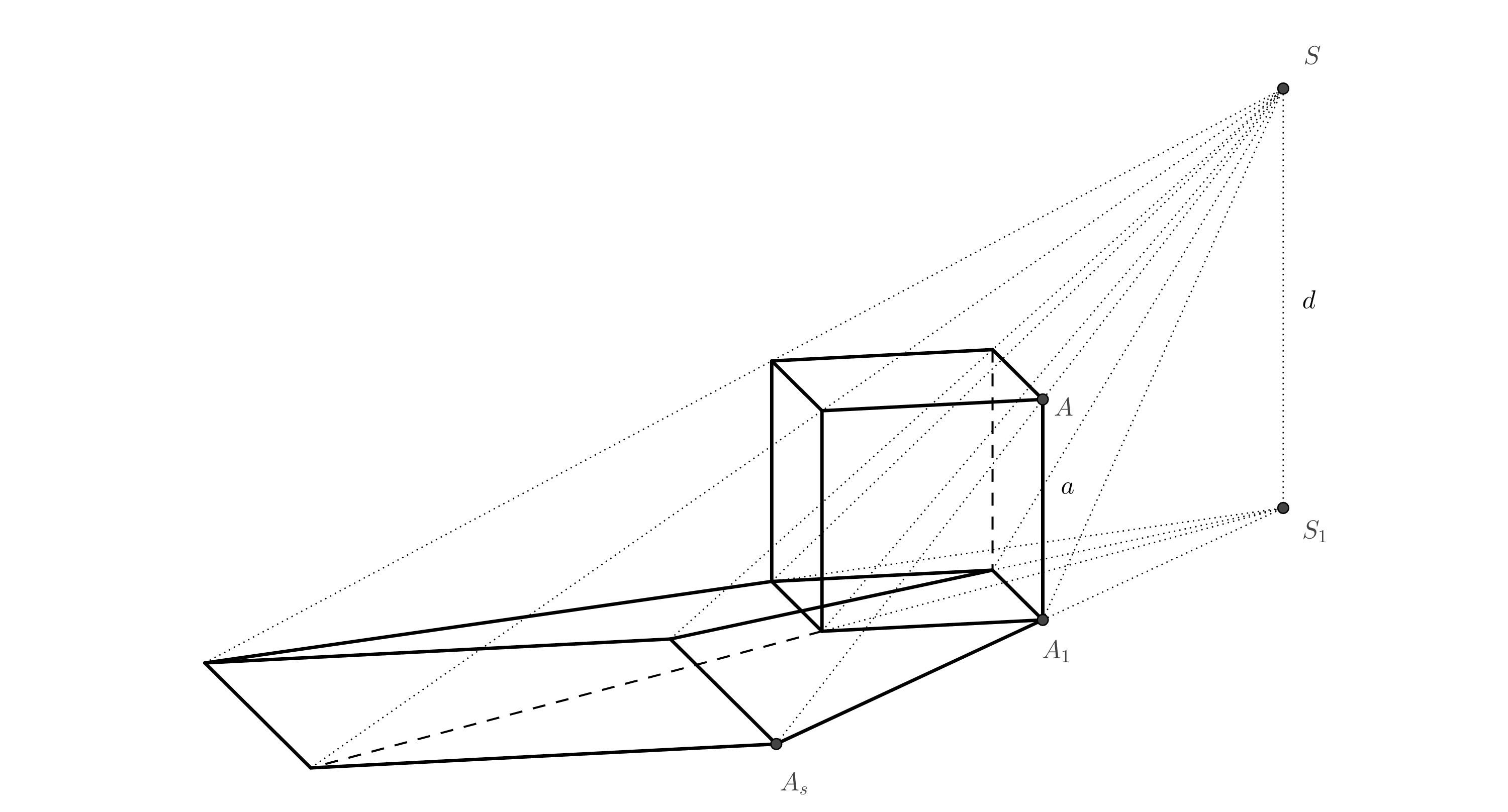
Exercise 4. Determine the anamorphosis of the cube. The square of the lower base is given by the opposite vertices \(A_1\), \(C_1\). Next, the position of the point \(S_1\) (the perpendicular projection of the projection center \(S\)) is given, the length \(d\) is given by the radius of the circle \(k\).
Solution. We construct a square \(A_1B_1C_1D_1\) with diagonal \(A_1C_1\). In the following figure, we see that point \(A_s\) is the intersection of lines \(AS\) and \(A_1S_1\). We know the lengths of the parallel sides of trapezoid \(A_1S_1SA\), so we can rotate it around side \(A_1S_1\) by \(90^\circ\) to the projection. The length \(S_1(S)=d\) is given by the radius of circle \(k\) and the length \(A_1(A)=a\) is the length of the side of square \(A_1B_1C_1D_1\). The point \(A_s\) is the intersection of line \(S_1A_1\) and line \((S)(A)\).
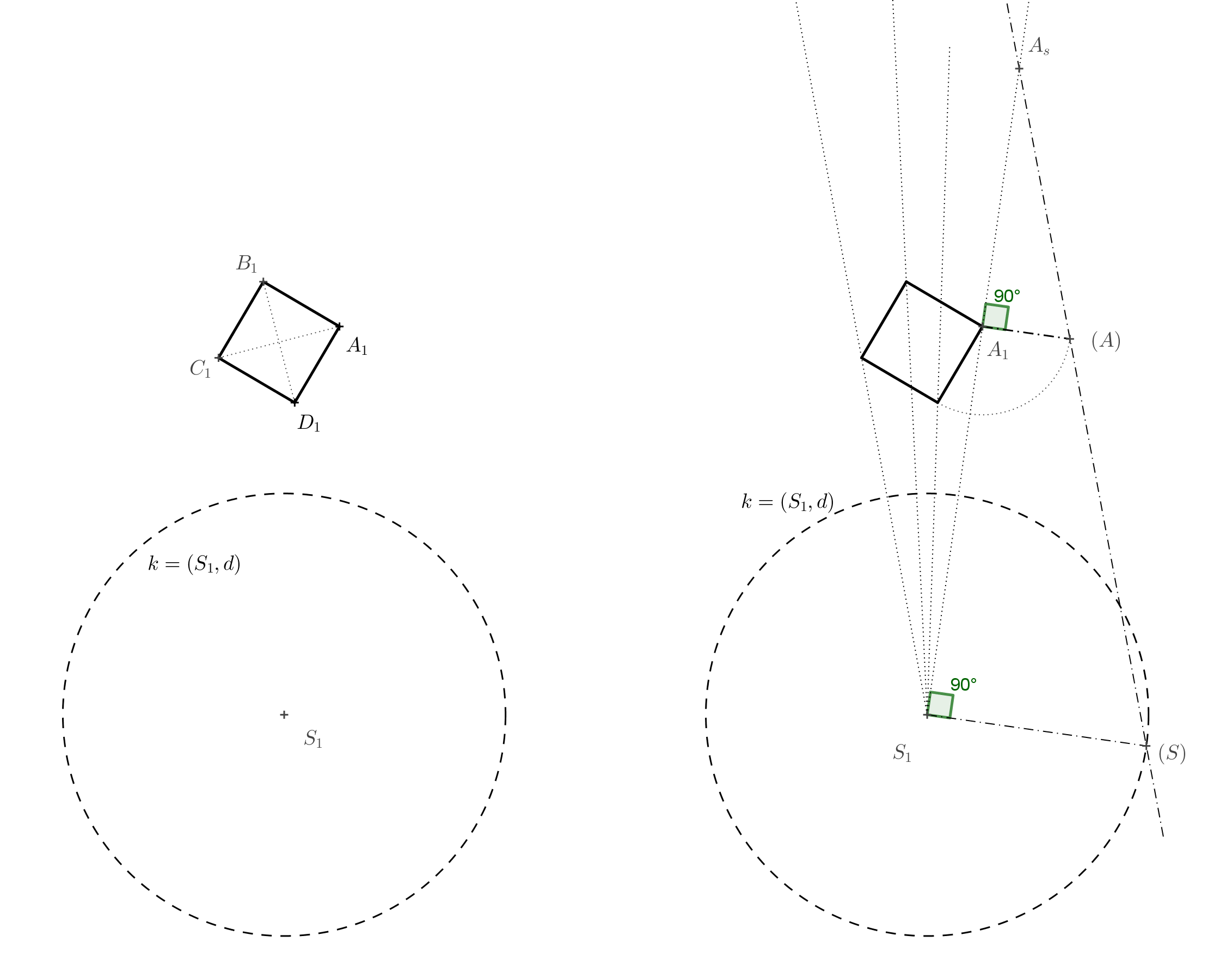
The square with vertex \(A_s\) is then drawn using homothety. The side edges of the cube correspond to the vertices of the squares that correspond to each other in homothety. We are done. However, if we want to support the illusion of a cube, we can draw another square that corresponds to square \(A_1B_1C_1D_1\) in homothety with center \(S\) and coefficient \(0<k<1\). If we color it gray, we will determine the shadow of the cube (when the direction of illumination is from above) and create the impression that the cube is levitating in space.
Exercise 5. Given two circles of different sizes, see the following figure for the assignment. Determine their center of symmetry \(S_1\) and their common tangents so that the resulting image is an anamorphosis of a cylinder.
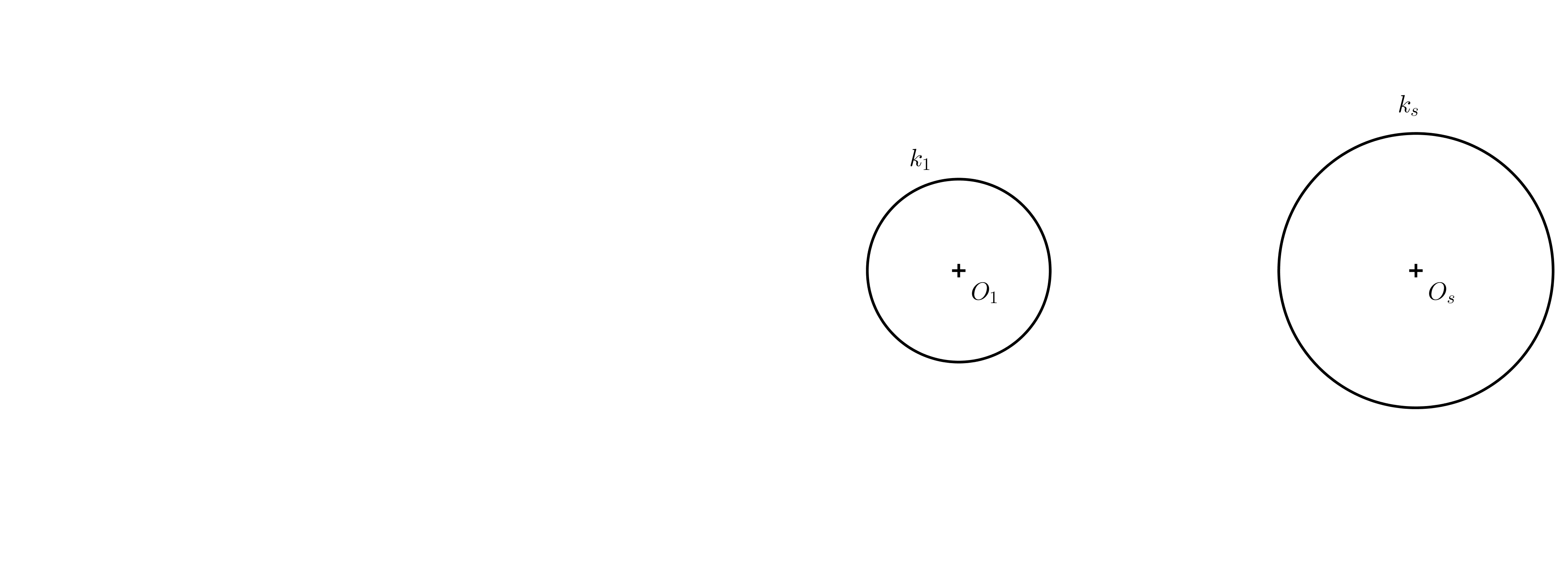
Solution. Any two non-concentric circles with different radii are homothetically related in two ways. We are interested in the way in which the colliding coefficient is positive. First, we construct the center of homothety (see the following figure).
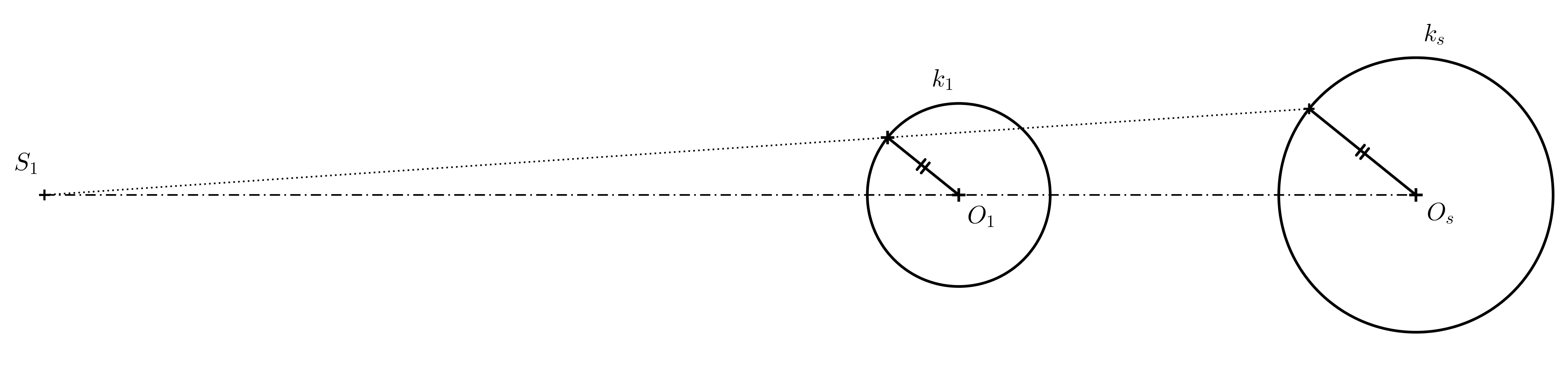
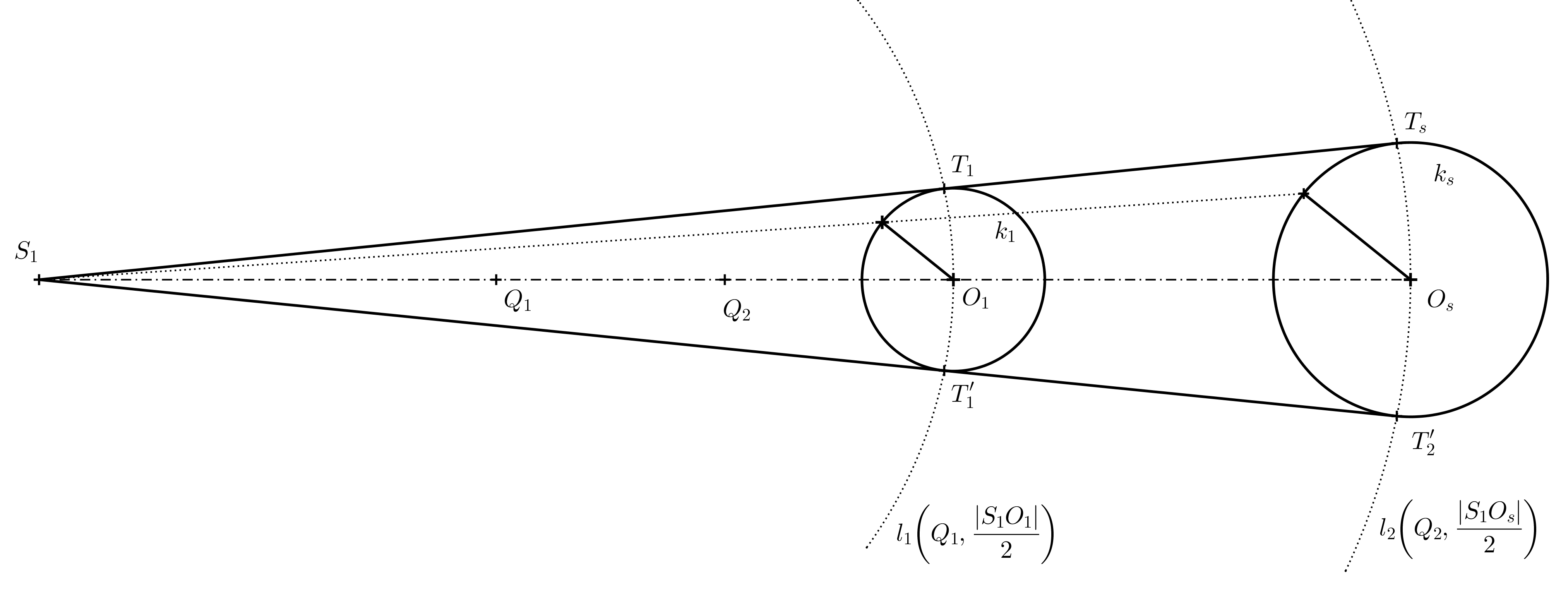
We find the points of contact on the Thales circles above the diameters \(S_1O_1\) and \(S_1O_s\). Only then do we draw the tangents (if we draw with a ruler and compass).
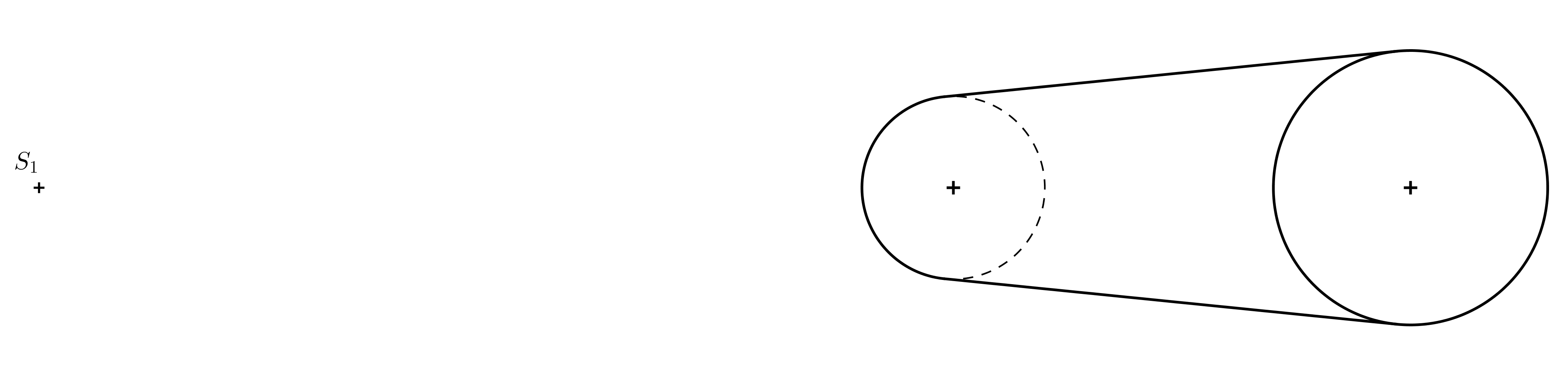
The resulting anamorphosis of the cylinder is shown in the following figure.
Exercise 6. The coefficient of homothety \(H(S,k)\) in the previous example, which maps \(O_1\) to \(O_s\), is \(k=1{.}5\). What must be the ratio \(d:v\), where \(d=\left|S_1S\right|\) and \(v=\left|O_1O\right|\) (the height of the imaginary cylinder in space), for the spatial illusion to work?
Solution. Let us denote \(x=\left|S_1O_1\right|\). Thanks to the homothety coefficient, we know that \(\left|S_1O_s\right|=1{,}5\,x\). This implies \(\left|O_1O_s\right|=0{,}5\,x\). Then we again use the similarity of triangles \(S_1O_s(S)\) and \(O_1O_s(O)\) in the following figure.
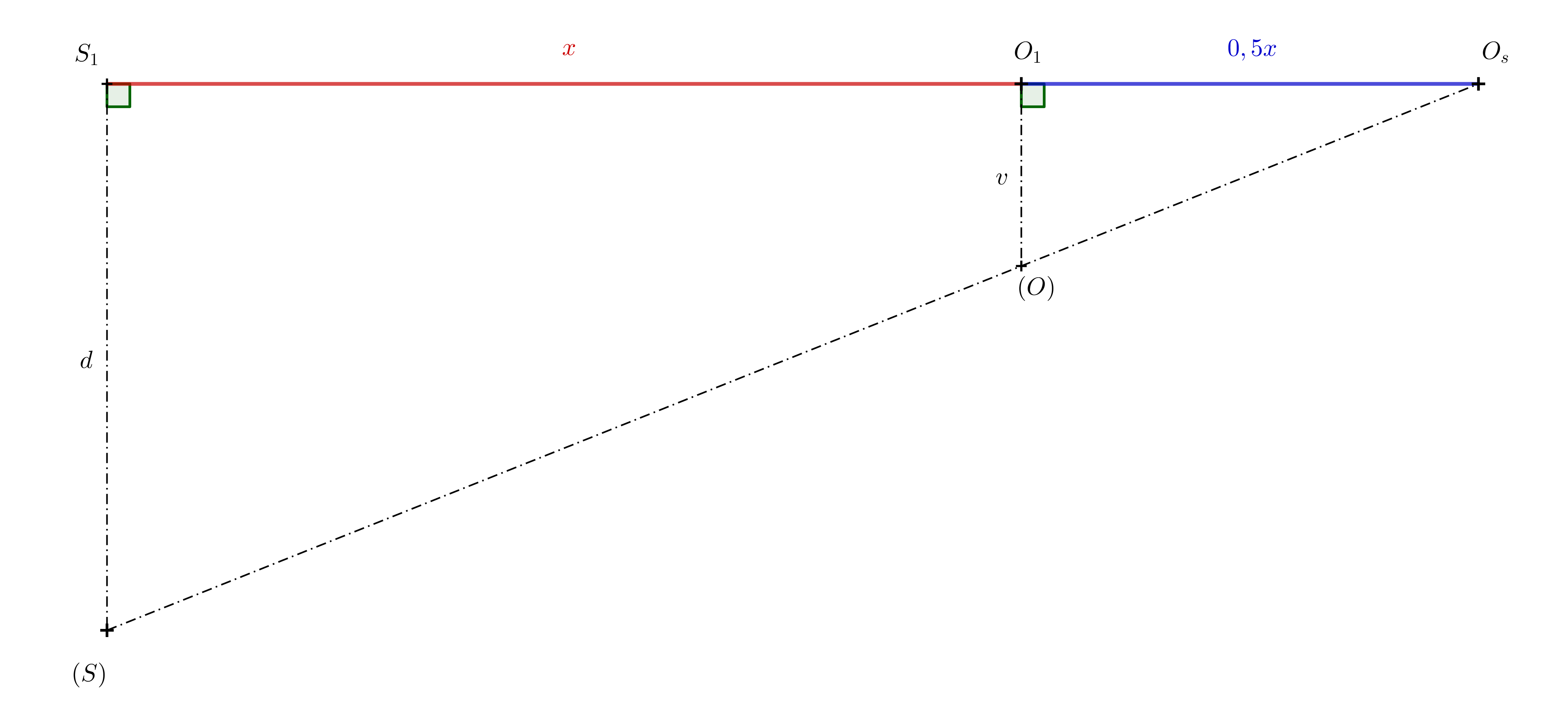
\[\frac{d}{v}= \frac{1{,}5\,x}{0{,}5\,x}=3\]
The ratio \(d:v\) must be equal to \(3:1\)
https://en.wikipedia.org/wiki/Anamorphosis
Ambassadors https://en.wikipedia.org/wiki/File:Hans_Holbein_the_Younger_-_The_Ambassadors_-_Google_Art_Project.jpg
Skull (detail of the painting The Ambassadors viewed from the correct location) https://en.wikipedia.org/wiki/File:Holbein_Skull.jpg
