Anamorfoza
 45 min.,
45 min.,  3/3
3/3 Anamorfoza w sztukach wizualnych
Anamorfoza to rodzaj sztuczki wizualnej lub sztuki, w której ukryty obraz ujawnia się, gdy patrzy się na niego pod określonym kątem. Anamorfoza opiera się na znalezieniu przez obserwatora odpowiedniego miejsca, z którego można patrzeć. Ten rodzaj sztuki ma długą i bogatą historię. Jednym z najbardziej znanych obrazów wykorzystujących anamorfozę jest „Ambasadorowie” (1533) niemieckiego malarza Hansa Holbeina Młodszego (1497–1543).

W dolnej części obrazu znajduje się dziwny, wydłużony obiekt. Można rozpoznać, co to jest, tylko stojąc przy ścianie w pobliżu prawej ramki obrazu i patrząc z tej strony. Jeśli znajdziesz odpowiednią pozycję, z której można patrzeć, zobaczysz, że jest to czaszka.
Sztuka anamorficzna może również wykorzystywać odbicia obrazów lub rzeźb w cylindrycznym lustrze1.
Pod koniec XX wieku sztuka anamorficzna przeżywała wielki renesans w fotografii, rysunku i instalacjach wielkoformatowych. Niektórzy artyści tworzą obrazy anamorficzne z przedmiotów codziennego użytku, takich jak urządzenia elektroniczne, buty i skarpety2. Anamorfozy pojawiają się również w sztuce ulicznej. Często są to rysunki na chodnikach, ulicach lub ścianach, które zaskakują i chwilowo dezorientują przechodniów. Może to być na przykład rysunek przypominający dziurę w ziemi, do której można wpaść, nogi wystające ze ściany lub kanału itp. Anamorfozy oparte na projekcji centralnej są bardziej przekonujące, gdy ogląda się je jednym okiem lub przez obiektyw aparatu. Jeśli jednak środek projekcji znajduje się wystarczająco daleko od obiektu, cieniowanie jest dobrze wykonane lub otoczenie wspiera iluzję przestrzeni, efekt staje się jeszcze bardziej realistyczny.
Praktyczne zastosowania
W przemyśle filmowym obiektywy anamorficzne są czasami wykorzystywane do kręcenia filmów. Zostały one pierwotnie zaprojektowane tak, aby obrazy szerokoformatowe w pełni wykorzystywały powierzchnię standardowych klatek filmu 35 mm. Bez nich obrazy panoramiczne pozostawiałyby niewykorzystaną górną i dolną część klatki. Pomimo pojawienia się cyfrowych czujników o wysokiej rozdzielczości, obiektywy anamorficzne są nadal używane ze względu na wyjątkowość uzyskiwanego obrazu.
Niektóre miasta wprowadziły przejścia dla pieszych, które z perspektywy nadjeżdżających kierowców wyglądały jak unoszące się w powietrzu pryzmaty. Po krótkim okresie próbnym przejścia te zostały w większości usunięte, ponieważ kierowcy mieli tendencję do zbyt gwałtownego hamowania podczas zbliżania się do nich.
Technika projekcji anamorficznej jest również stosowana na niektórych stadionach sportowych, gdzie wykorzystuje się ją do celów reklamowych. Logo firm są malowane bezpośrednio na boisku, a pod kątem kamery telewizyjnej tekst wydaje się stać pionowo na powierzchni.
Anamorfozy podstawowych brył
W poniższym tekście i przykładach stworzymy anamorfoty podstawowych brył za pomocą projekcji centralnej na płaszczyznę. Płaszczyzna, na której narysujemy te anamorficzne obrazy, nazywana jest płaszczyzną projekcji. W naszym przypadku płaszczyzną projekcji będzie kartka papieru, na której rysujemy, co naturalnie ogranicza rozmiar obiektów, które możemy stworzyć. Następnie będziemy obserwować powstałe obrazy przez oko aparatu za pomocą telefonu komórkowego lub aparatu fotograficznego. Jeśli masz taką możliwość, możesz tworzyć obrazy anamorficzne na zewnątrz, najlepiej z dala od dróg i ruchu ulicznego.
Piramida i stożek
Być może najłatwiejszymi bryłami do tworzenia obrazów anamorficznych są piramida i stożek — pod warunkiem, że ich podstawy leżą w płaszczyźnie rzutu. Wyjaśnijmy tę zasadę na przykładzie piramidy. Oprócz samej bryły musimy również zdefiniować środek rzutu \(S\) i jego rzut prostopadły na płaszczyznę rzutu \(S_1\). Środek rzutu można traktować jako oko obserwatora, a rzut prostopadły jako miejsce, w którym stoi obserwator. Odległość \(S _1S = d\) jest zatem odległością od płaszczyzny rzutu do środka rzutu. W przypadku regularnej piramidy kwadratowej jej wierzchołek oznaczamy jako \(V\) ,a rzut prostopadły wierzchołka na płaszczyznę rzutu jako \(V_1\). Punkt przecięcia linii \(SV\) (zwanej promieniem rzutu) z płaszczyzną rzutu otrzymujemy jako punkt przecięcia linii \(SV\) i \(S_1V_1\) (patrz rysunek po lewej stronie). Przydatne jest naszkicowanie takiego diagramu, aby zrozumieć, jak działa złudzenie optyczne i jak będzie wyglądał rzut centralny. Jednak ten obraz przestrzenny nie jest potrzebny do określenia anamorfozy piramidy.
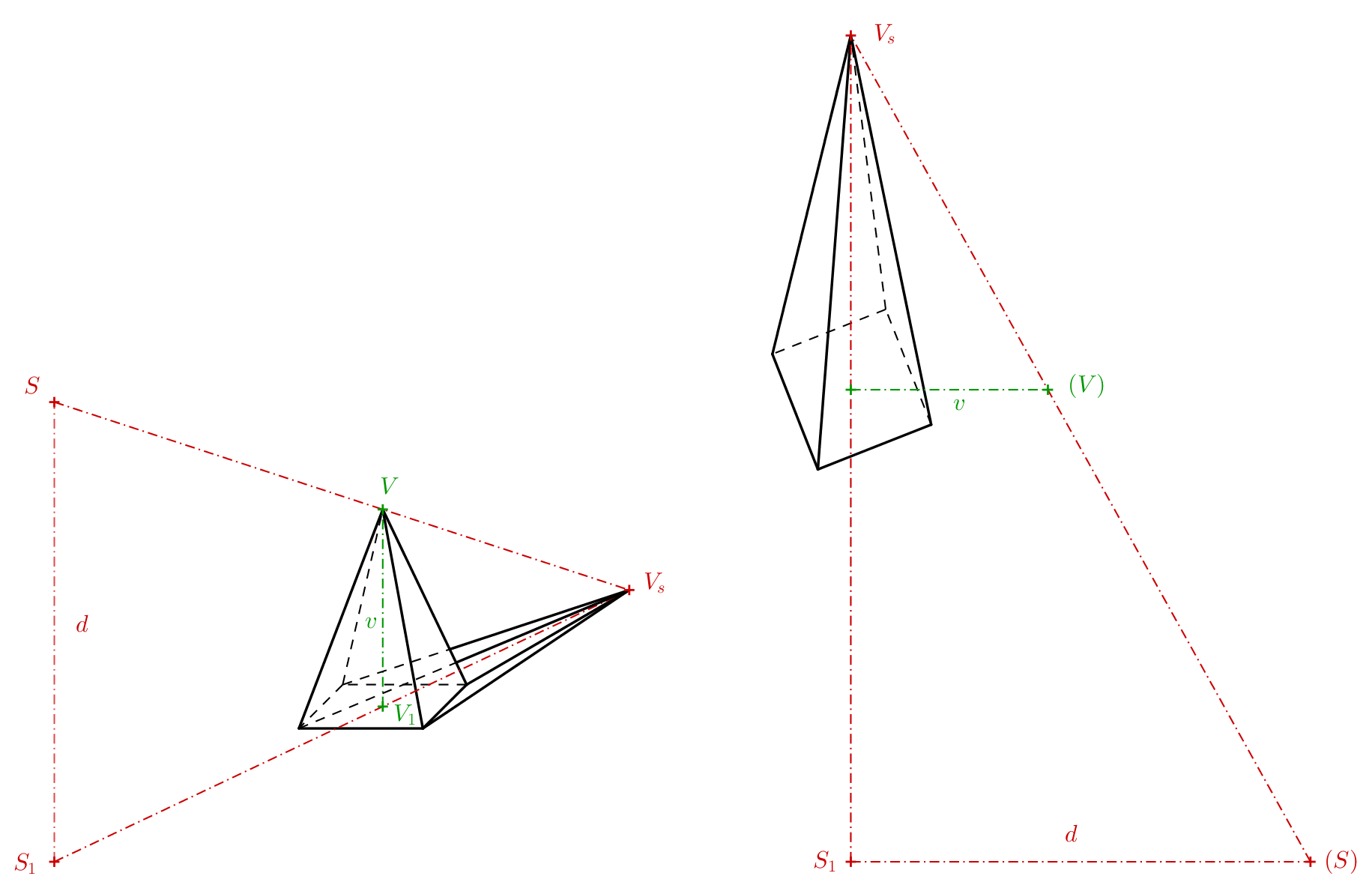
W rzeczywistości potrzebujemy tylko trapezu \(S_1V_1VS\), który można również przedstawić w płaszczyźnie rzutu jako trapez \(S_1V_1(V)(S)\) (patrz poprzedni rysunek po prawej stronie). Punkty, które wcześniej znajdowały się w przestrzeni poza rzutem (punkty \(V\) i \(S\)), są teraz pokazane w nawiasach w rzucie, aby je odróżnić. Punkty \((V)\) i \((S)\) powstały w wyniku obrotu płaszczyzny \(S_1VS\) o \(90^\circ\) w projekcji wokół linii \(S_1V_1\). Jeśli znamy wysokość piramidy, odległość oka obserwatora od płaszczyzny rzutu oraz odległość \(S_1V_1\), możemy narysować trapez. Przedłużając jego nierównoległe boki, znajdujemy punkt \(V_s\).
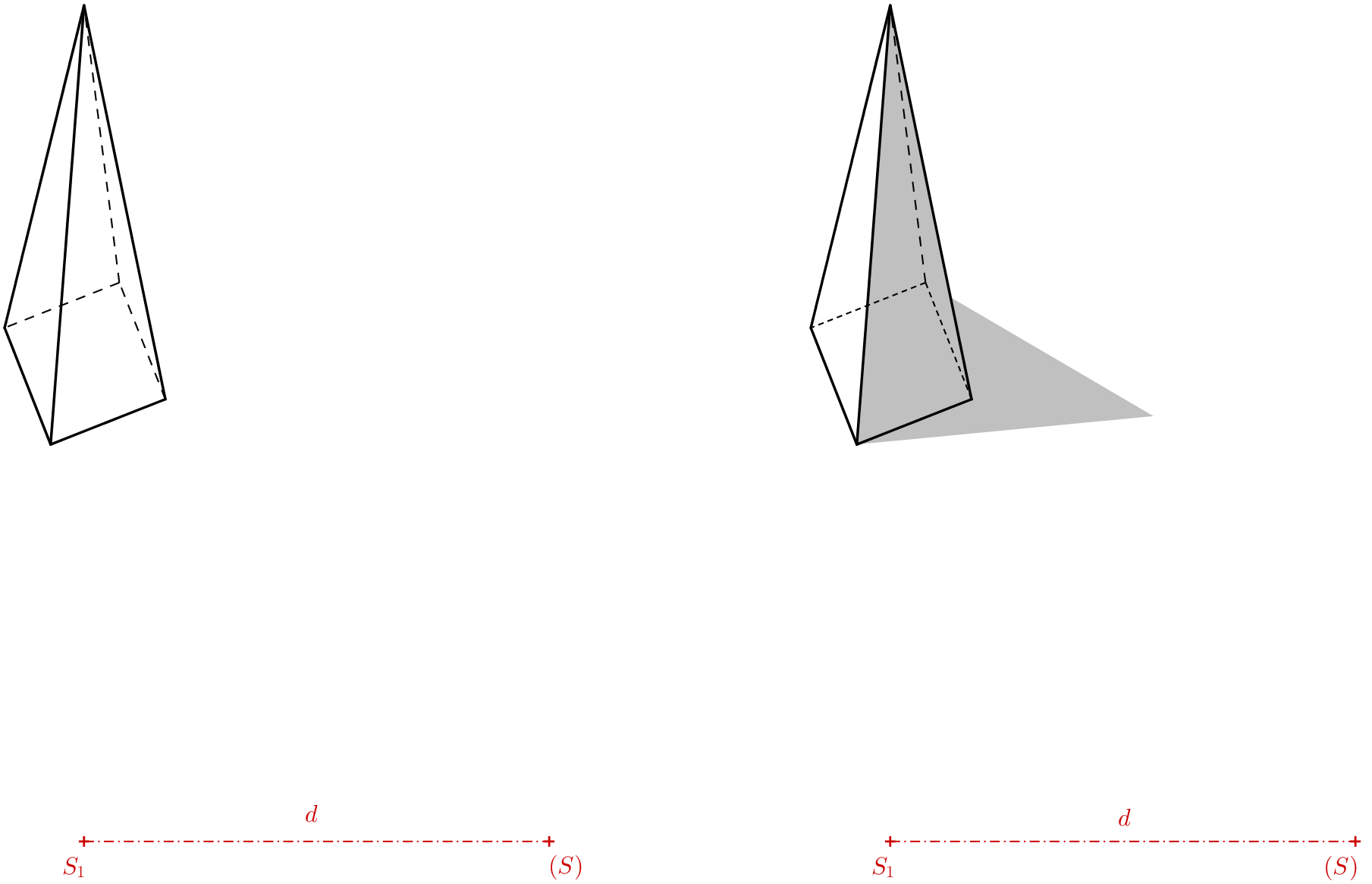
Wynik (patrz poprzedni rysunek po lewej stronie) należy narysować bez linii konstrukcyjnych. Następnie możemy go obserwować przez obiektyw aparatu fotograficznego. Patrząc przez aparat, stwierdzamy, że ukryte krawędzie dolnej podstawy najlepiej narysować gęstszą linią przerywaną niż rzut niewidocznej krawędzi bocznej. Aby piramida wyglądała bardziej realistycznie, możemy cieniować obraz. Cień można oszacować dowolnie, a cień rzucany przez wierzchołek można dobrać według potrzeb. Anamorfoza piramidy jest gotowa. Aby iluzja zadziałała, obiektyw aparatu musi być umieszczony bezpośrednio nad punktem \(S_1\) na wysokości równej odległości \(S_1(S)\). Obraz widziany przez aparat powinien przypominać ten pokazany na poniższym rysunku.

Ćwiczenie 1. Chcemy narysować na ziemi kształt, który widziany w przestrzeni wygląda jak stożek o wysokości \(1\,\mathrm{m}\) i podstawie o promieniu \(r=0{.}4\,\mathrm{m}\). Tak jak poprzednio, środek rzutu oznaczamy literą \(S\), a jego rzut prostopadły na ziemię literą \(S_1\). Zakładamy, że oko przeciętnego obserwatora znajduje się na wysokości \(150\,\mathrm{cm}\) nad ziemią. W jakiej odległości musi znajdować się \(V_s\) od \(V_1\) (\(V_s\) jest rzutem centralnym wierzchołka stożka na płaszczyznę rzutu, \(V_1\) jest rzutem prostopadłym wierzchołka stożka na płaszczyznę rzutu), zakładając, że obserwator stoi w odległości \(3\) metrów od punktu \(V_1\)?
Rozwiązanie. Trójkąty \(S_1V_sS\) i \(V_1V_sV\) są podobne.

W związku z tym stosunki odpowiednich boków są równe:
\[\frac{x}{1}= \frac{x+3}{1{.}5},\]
\[1{.}5\,x=x+3,\]
z czego otrzymujemy \(x=6\). Odległość punktu \(V_s\) od \(V_1\) musi wynosić \(6\) metrów.
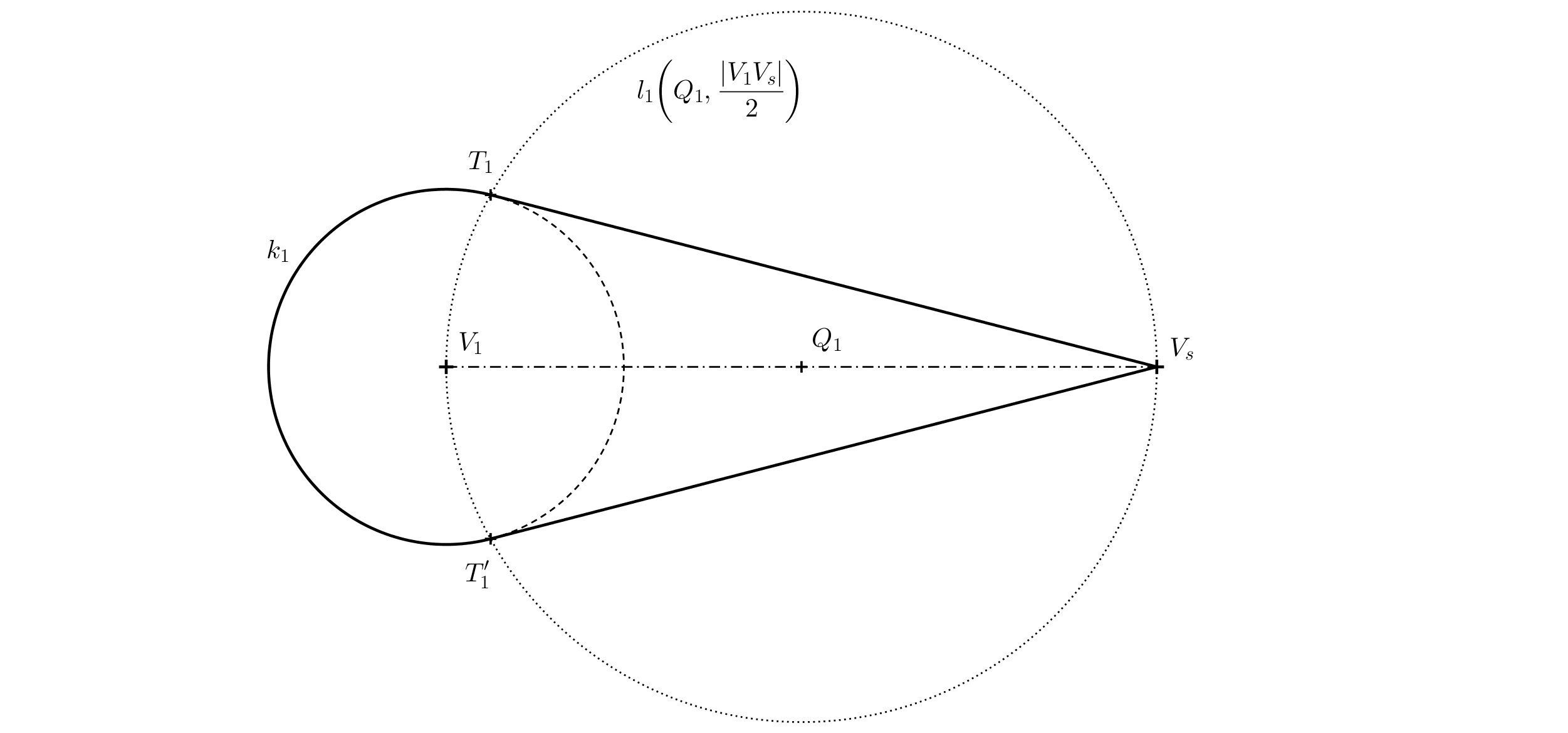
Ćwiczenie 2. Mamy okrąg podstawowy \(k\) o środku \(V_1\) i punkcie \(V_s\) (patrz rysunek poniżej). Wyobraź sobie prosty stożek w przestrzeni o okręgu podstawowym \(k\) i środku rzutu \(S\), tak że \(V_s\) jest rzutem centralnym wierzchołka stożka. Punkt \(V_1\) jest rzutem prostopadłym wierzchołka stożka na płaszczyznę rzutu (tj. kartkę papieru). Określ obrys rzutu centralnego stożka.

Rozwiązanie. Obrys stożka (z wyjątkiem części okręgu podstawowego) będzie składał się z stycznych do wierzchołka \(V_s\). Dokładniej rzecz biorąc, będą to linie łączące punkt \(V_s\) z punktami styczności \(T\) i \(T'\), które otrzymujemy jako punkty przecięcia okręgu Thalesa \(l\) zbudowanego nad średnicą \(V_1V_s\) i okręgu podstawowego \(k\).
Ćwiczenie 3. Aby rozwiązać poprzedni problem, określ położenie punktu \(S\) (wykorzystując \(S_1\) i \((S)\)), jeśli znana jest wysokość \(v\) stożka w przestrzeni oraz odległość \(d=\left|S_1S\right|\). Patrz poniższy rysunek jako odniesienie, długości \(v\) i \(d\) są podane jako odcinki.
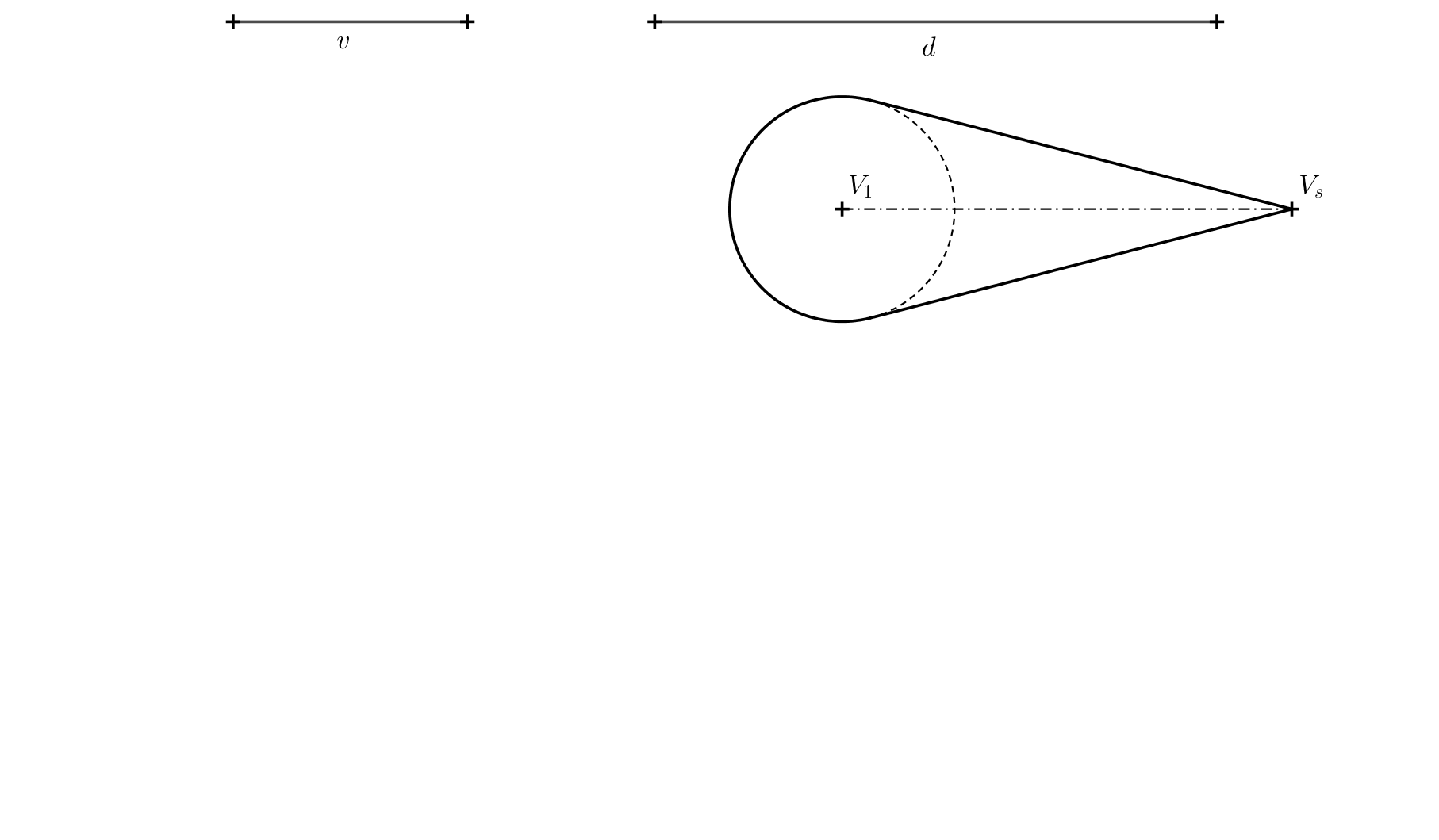
Rozwiązanie. Punkt \(S\) musi spełniać dwa warunki: jego odległość od płaszczyzny rzutu jest równa \(d\) i musi leżeć na prostej \(VV_s\). Punkty \(S\), podobnie jak punkt \(V\), leżą w płaszczyźnie prostopadłej do płaszczyzny rzutu. Przecięciem tych dwóch płaszczyzn jest prosta \(o=V_1V_s\). Możemy obrócić wierzchołek \(V\) o \(90^\circ\) wokół tej prostej do płaszczyzny rzutu. Obrócony obraz punktu \(V\) oznaczamy jako \((V)\). Musi on leżeć w odległości \(v\) od punktu \(V_1\), na prostopadłej do osi \(o\). W odległości \(d\) od osi \(o=V_1V_s\) rysujemy linię \(p\). Punkt \((S)\) musi leżeć na przecięciu linii \(p\) i odcinka \((V)V_s\).

Pryzmat i cylinder
Aby skonstruować obraz anamorficzny pryzmatu lub cylindra, używamy homotezji. Wyjaśnijmy dlaczego, posługując się przykładem sześcianu pokazanego na rysunku.
Między górną ścianą sześcianu a jego rzutem w przestrzeni istnieje podobieństwo, którego punktem podobieństwa jest punkt \(S\) (wynika to z podobieństwa trójkątów). Ponieważ dolna ściana sześcianu jest również rzutem prostopadłym górnej ściany na płaszczyznę rzutu, między dolną ścianą a środkowym rzutem górnej ściany istnieje podobieństwo, którego punktem podobieństwa jest punkt \(S_1\).
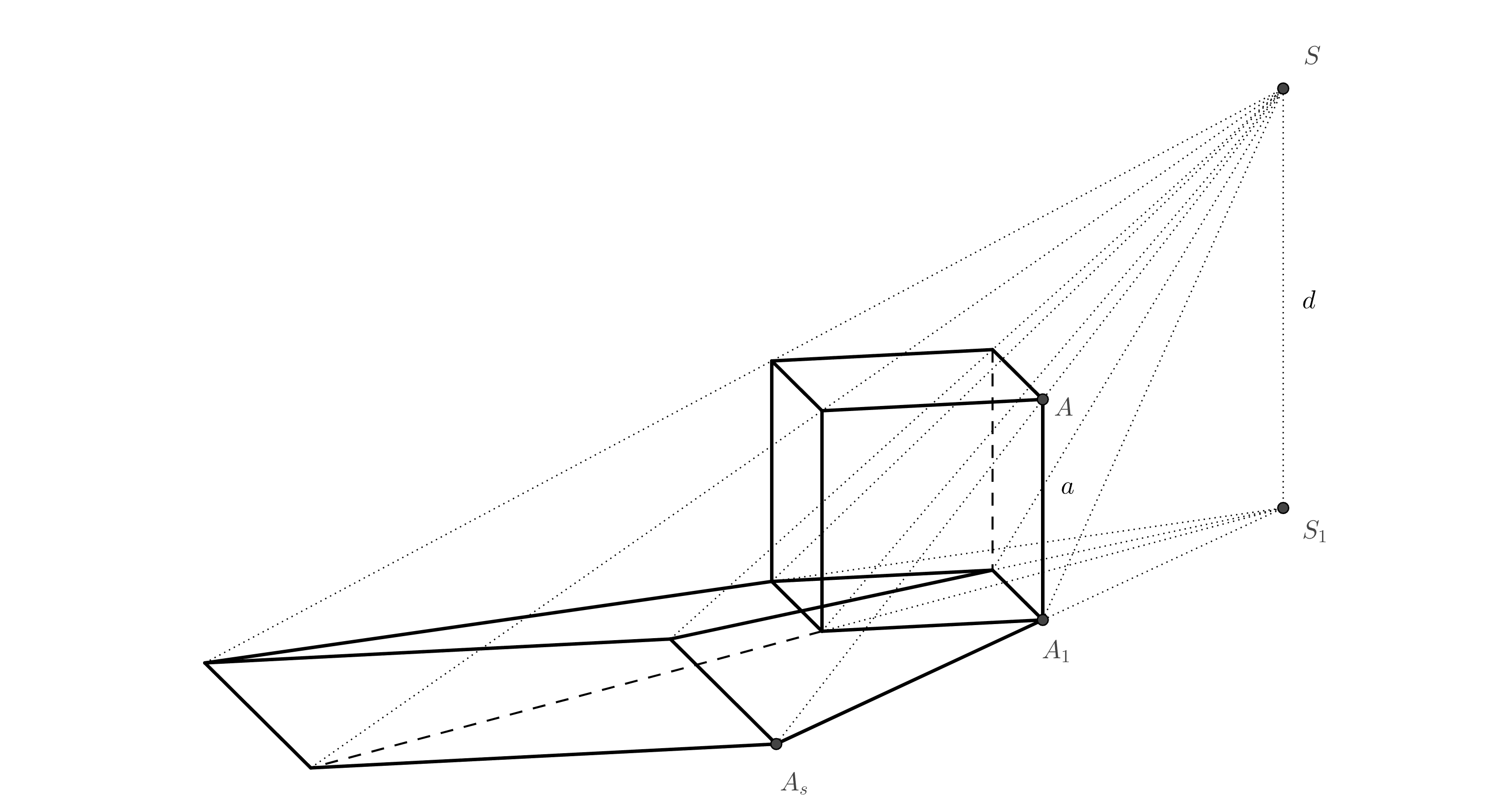
Ćwiczenie 4. Określ projekcję anamorficzną sześcianu. Podstawa kwadratowa jest określona przez dwa przeciwległe wierzchołki \(A_1\) i \(C_1\). Określono również położenie punktu \(S_1\) (projekcja prostopadła środka projekcji \(S\)). Długość \(d\) jest określona przez promień okręgu \(k\).
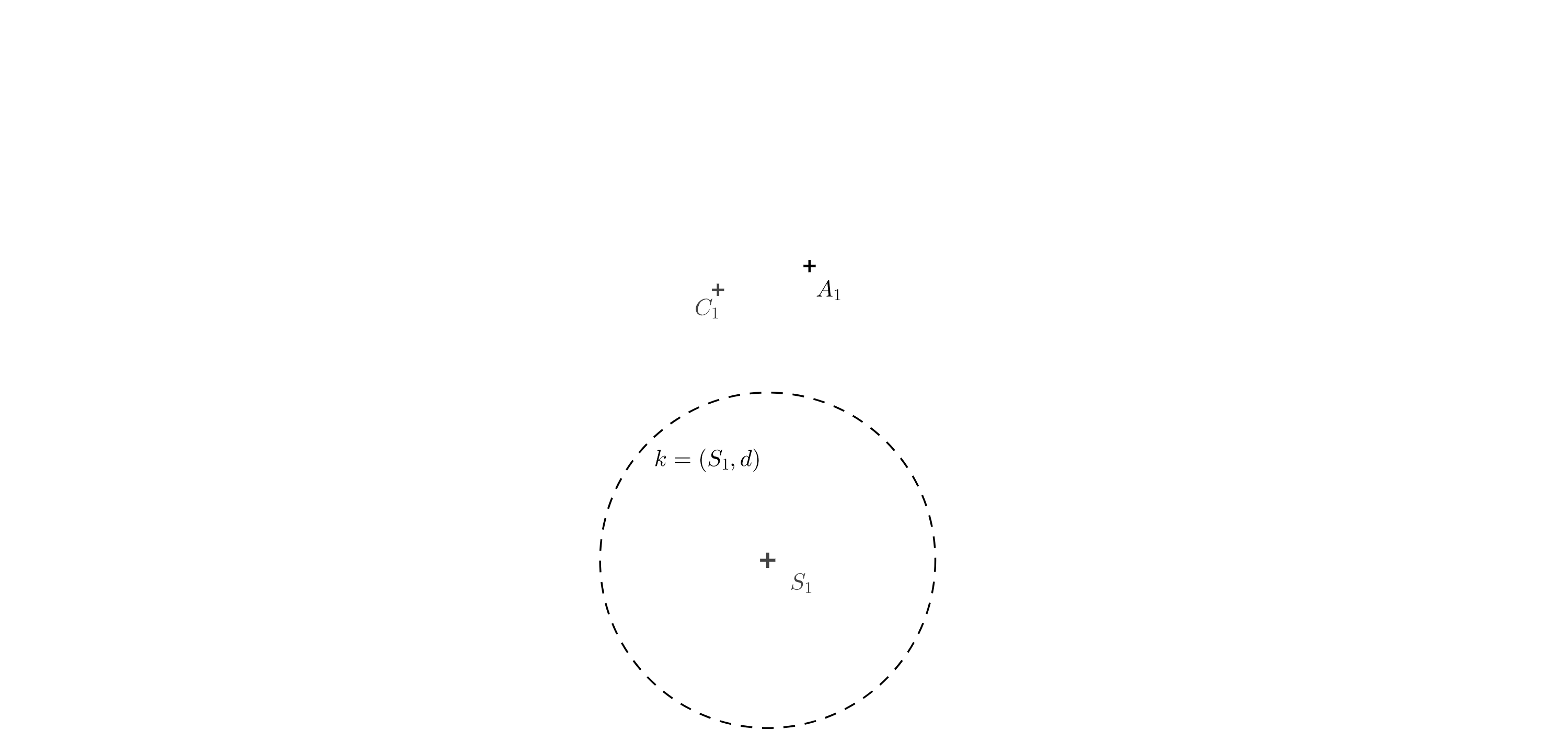
Rozwiązanie. Najpierw narysuj kwadrat \(A_1B_1C_1D_1\) z przekątną \(A_1C_1\). Na poprzednim rysunku widzimy, że punkt \(A_s\) jest przecięciem linii \(AS\) i \(A_1S_1\). Ponieważ znamy długości równoległych boków trapezu \(A_1S_1SA\), możemy obrócić go o \(90^\circ\) wokół boku \(A_1S_1\) do płaszczyzny rzutu. Długość \(S_1(S)=d\) jest dana przez promień okręgu \(k\), a długość \(A_1(A)=a\) jest długością boku kwadratu \(A_1B_1C_1D_1\). Punkt \(A_s\) jest punktem przecięcia prostej \(S_1A_1\) i prostej \((S)(A)\).
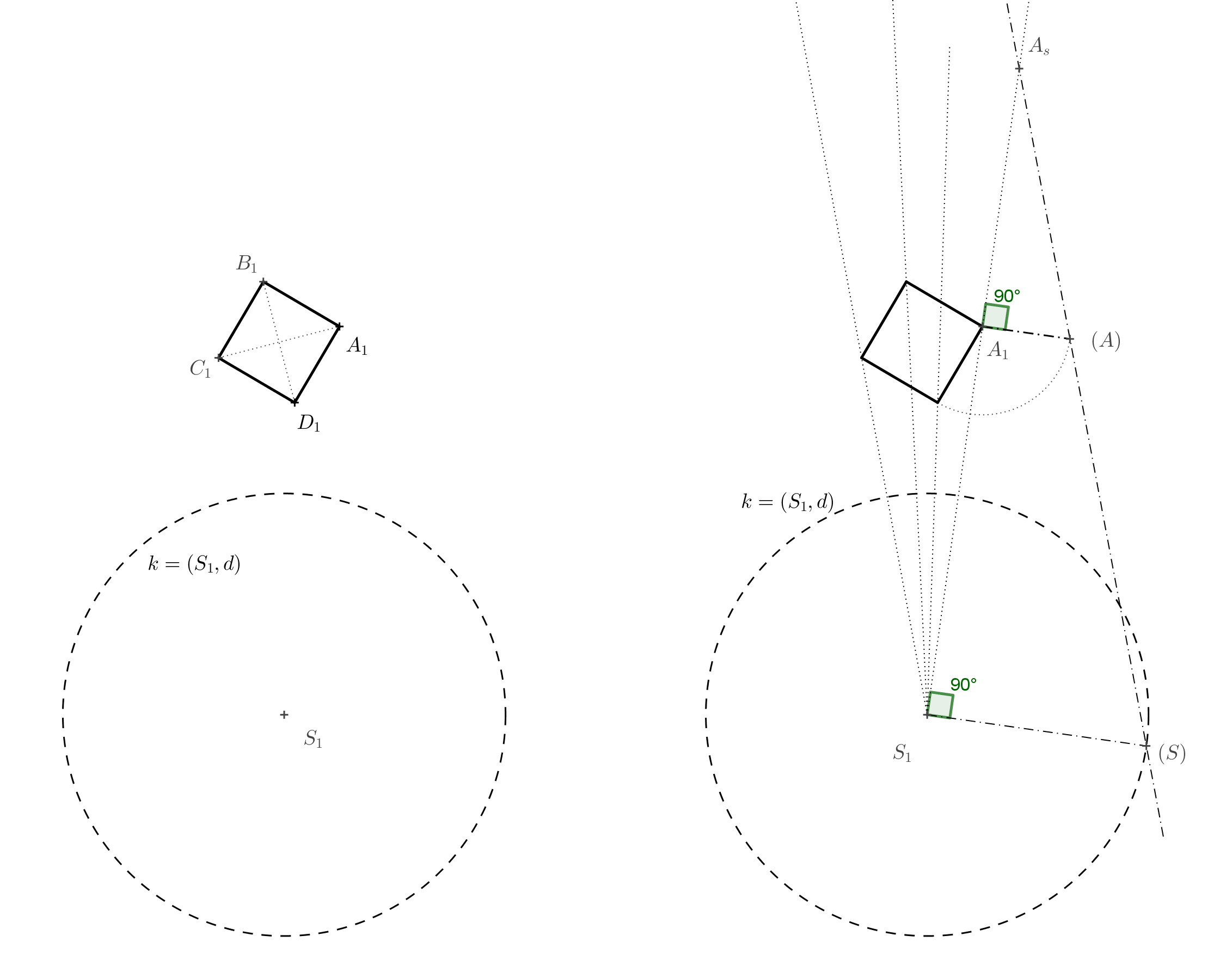
Następnie rysujemy kwadrat o wierzchołku \(A_s\) za pomocą homotezji. Boczne krawędzie sześcianu odpowiadają liniom łączącym pasujące wierzchołki pierwotnego kwadratu i jego obrazu w danej homotezji. I gotowe. Jeśli jednak chcemy wzmocnić iluzję sześcianu, możemy narysować kolejny kwadrat odpowiadający kwadratowi \(A_1B_1C_1D_1\) w homotezji o środku \(S\) i współczynniku \(0<k<1\). Jeśli ten kwadrat pokolorujemy na szaro, będzie on pełnił rolę cienia sześcianu (zakładając oświetlenie od góry), pomagając stworzyć wrażenie, że sześcian unosi się w przestrzeni.

Ćwiczenie 5. Mamy dwa okręgi o różnych rozmiarach (patrz rysunek poniżej). Określ ich środek homotezji \(S_1\), który odwzorowuje jeden okrąg na drugi, i narysuj ich wspólne styczne tak, aby wynikowy obraz był anamorfoza cylindra.
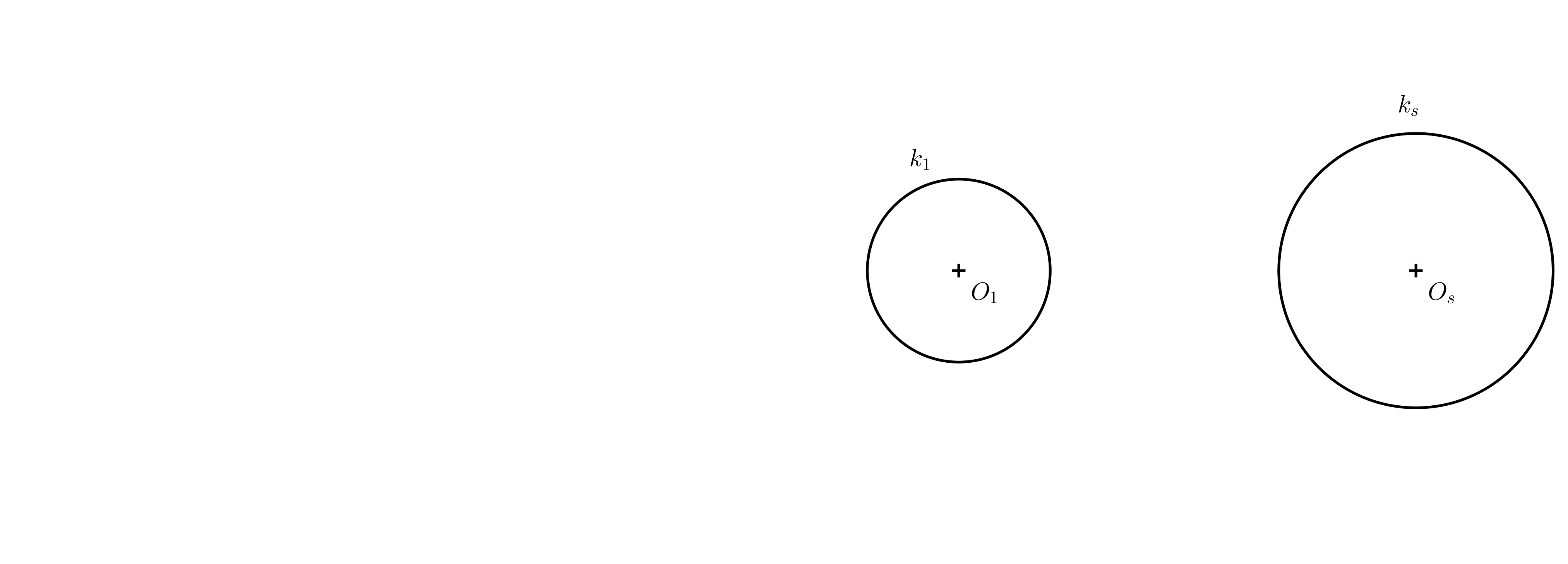
Rozwiązanie. Dowolne dwa niekoncentryczne okręgi o różnych promieniach są homotetycznie powiązane na dwa sposoby. Interesuje nas sposób, w jaki stosunek homotetyczności jest dodatni. Najpierw konstruujemy środek homotetyczności (patrz poniższy rysunek).
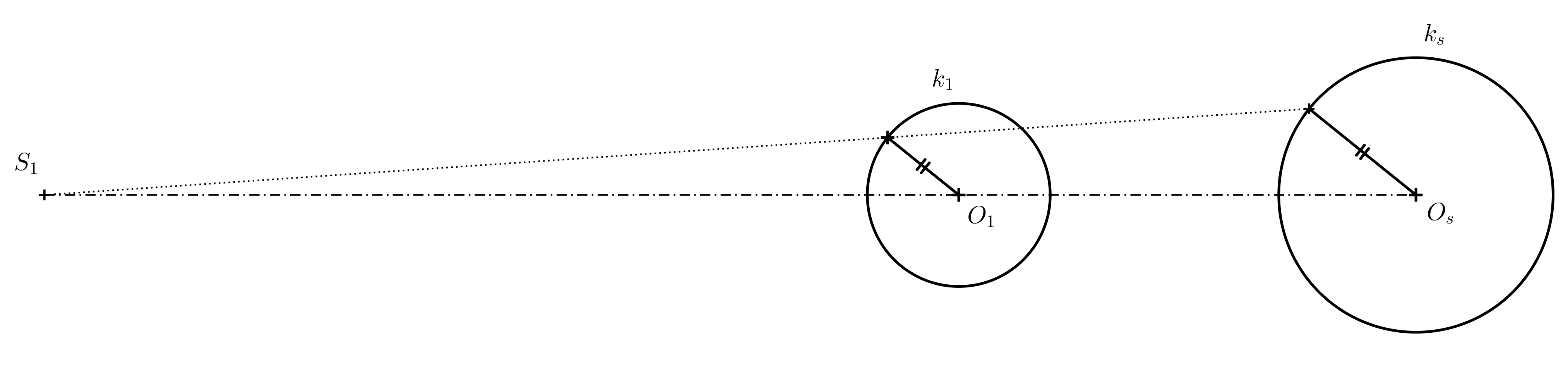
Punkty styczności znajdują się na okręgach Thalesa wykreślonych na średnicach \(S_1O_1\) i \(S_1O_s\). Dopiero wtedy rysujemy styczne (jeśli używamy linijki i cyrkla).
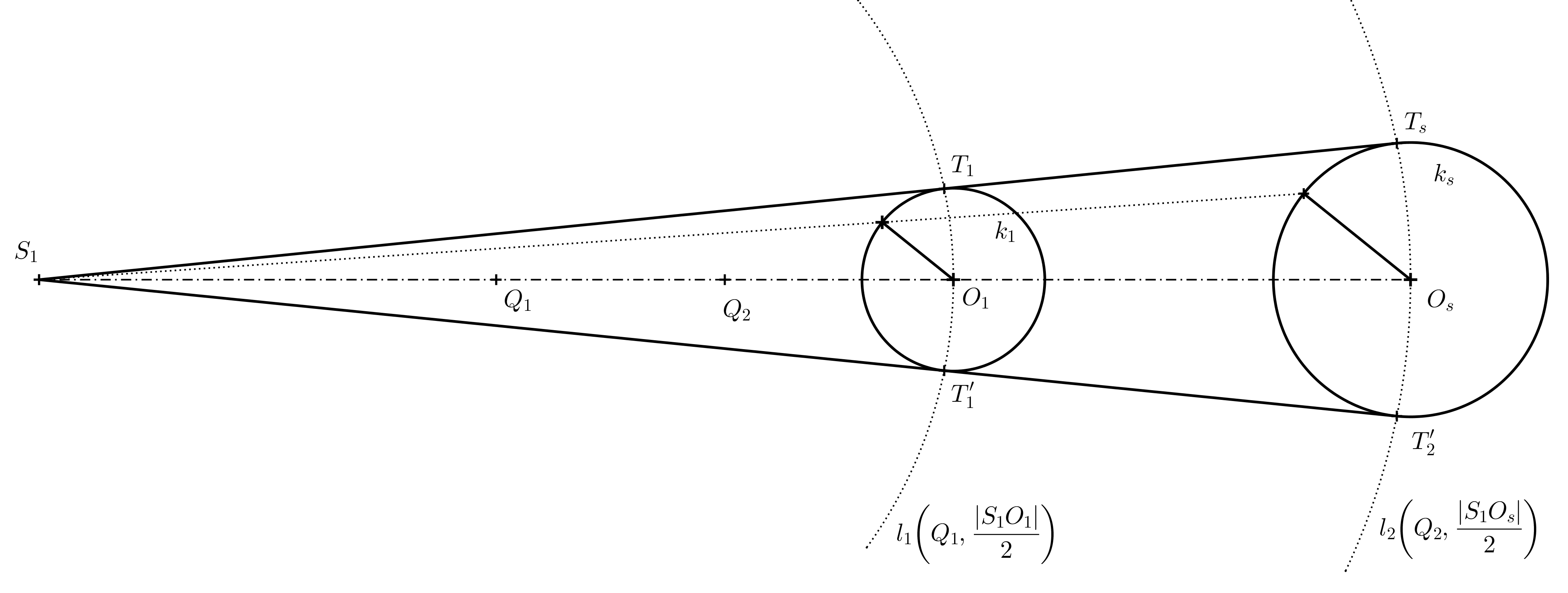
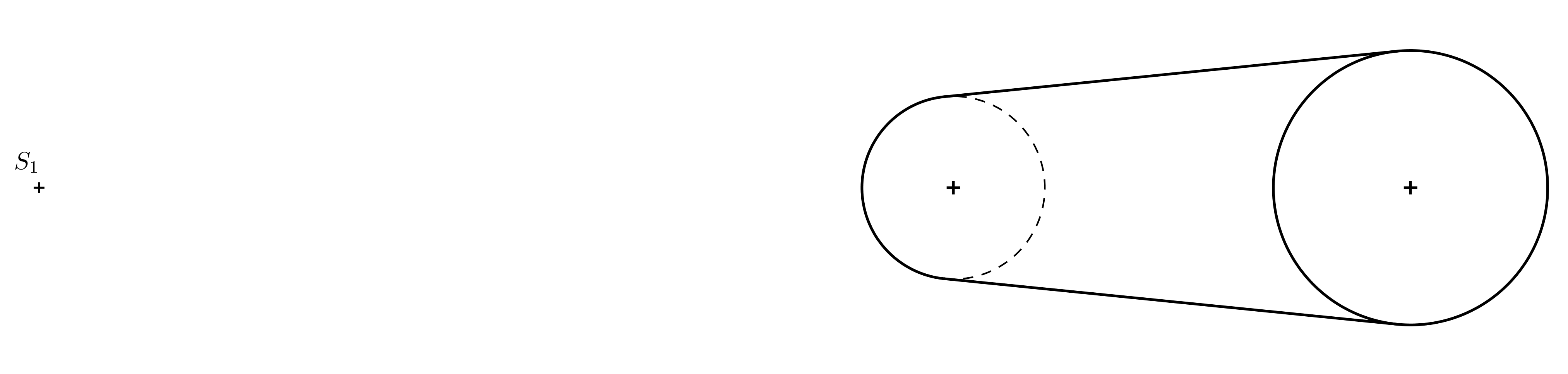
Wynikowa anamorfozacja cylindra została przedstawiona na poniższym rysunku.
Ćwiczenie 6. Współczynnik homotezji \(H(S,k)\) z poprzedniego ćwiczenia, który odwzorowuje punkt \(O_1\) na \(O_s\), wynosi \(k=1{.}5\). Jaki musi być stosunek \(d:v\), gdzie \(d=\left|S_1S\right|\) i \(v=\left|O_1O\right|\) (wysokość wyobrażonego cylindra w przestrzeni), aby iluzja przestrzenna zadziałała?
Rozwiązanie. Oznaczmy \(x=\left|S_1O_1\right|\). Ponieważ współczynnik homotezji wynosi \(k=1{.}5\), wynika z tego, że \(\left|S_1O_s\right|=1{.}5\,x\). Oznacza to, że \(\left|O_1O_s\right|=0{.}5\,x\). Następnie ponownie wykorzystujemy podobieństwo trójkątów \(S_1O_s(S)\) i \(O_1O_s(O)\) na poniższym rysunku.
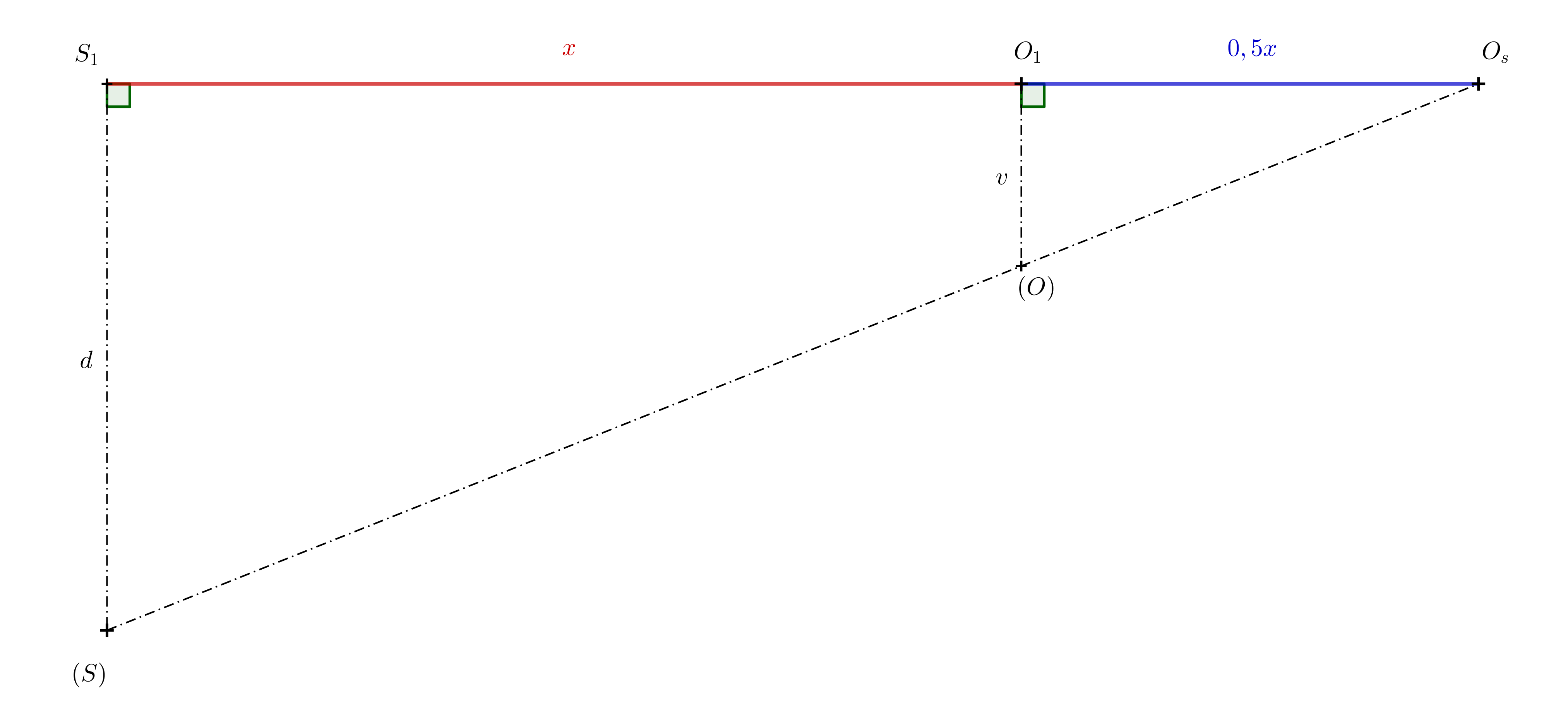
\[\frac{d}{v}= \frac{1{.}5\,x}{0{.}5\,x}=3\]
Stosunek \(d:v\) musi wynosić \(3:1\).
Referencje i literatura
Literatura
https://en.wikipedia.org/wiki/Anamorphosis
Źródła zdjęć
Ambasadorowie https://en.wikipedia.org/wiki/File:Hans_Holbein_the_Younger_-_The_Ambassadors_-_Google_Art_Project.jpg
Czaszka (fragment obrazu Ambasadorowie oglądany z właściwej pozycji) https://en.wikipedia.org/wiki/File:Holbein_Skull.jpg