Logické obvody
 35 min.,
35 min.,  2/3
2/3 Ktoré kúzlo dokáže v preťaženom výťahu rozsvietiť správnu kontrolku, stlačením tlačidla automatu pripraviť pomarančovú šťavu, po pár minútach zhasnúť rozsvietené svetlá v chodbe domu alebo pohybovať s postavou na obrazovke počítača? O tieto a celú radu ďalších činností sa v reálnom živote starajú logické obvody, ktoré podrobnejšie preskúmame v nasledujúcej sérii úloh. Logické obvody sa skladajú z tzv. logických členov, ktoré realizujú logické operácie. V úlohách budeme pracovať iba s tromi základnými logickými členmi NOT (negácia), AND (konjunkcia) a OR (disjunkcia). Na obrázku sú vidieť ich príslušné symboly (podľa americkej normy ANSI/MIL) v logických obvodoch. Sú orientované tak, aby smer vstupu bol zľava. Vstupy chápeme ako výroky a výstupy sú potom zložené výroky.

Pravdivostné hodnoty sú v logických obvodoch realizované napätím. Nízke napätie označuje pravdivostnú hodnotu 0 a vysoká úroveň napätia označuje hodnotu 1. Pokiaľ je napr. u člena AND na vstupe A nízka úroveň napätia a na vstupe B vysoká úroveň, je na výstupe nízka úroveň napätia. Konkrétne hodnoty úrovní sa líšia podľa konkrétneho využitia obvodu. Bežná je napríklad nízka úroveň približne 0V a vysoká približne 5V. Na ďalšom obrázku vidíme znázornenie jedného zložitejšieho logického obvodu. Pre názornosť je v obrázku tiež vyznačené postupné skladanie výrokov, čo zodpovedá vstupom alebo výstupom jednotlivých členov. Čierna bodka označuje uzol, v ktorom sa logický obvod vetví. Výstup jedného člena tak môže byť privedený na viac vstupov zároveň.
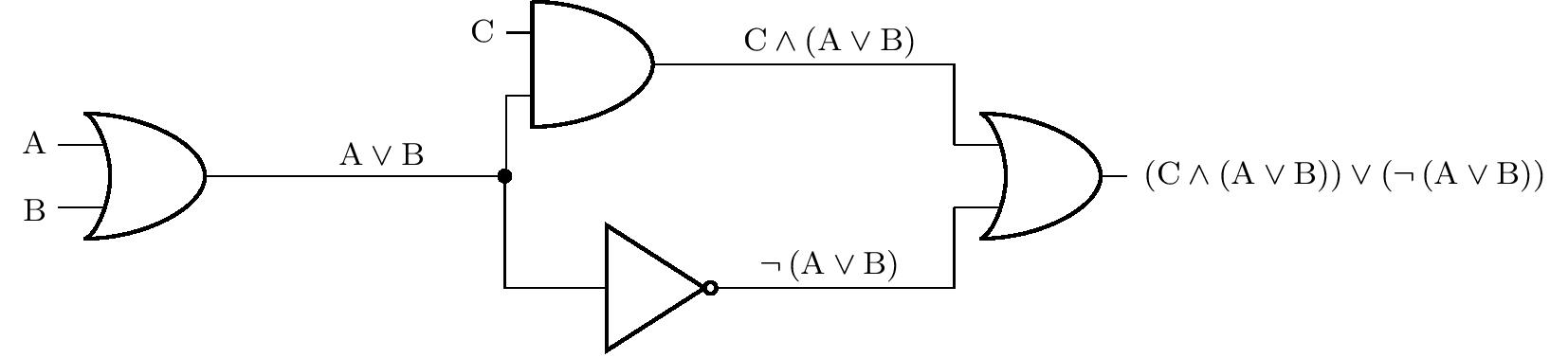
V nasledujúcich úlohách môžu byť pred vstupmi zaradené spínače alebo tlačidlá a za výstupmi logického obvodu potom môžu byť zaradené žiarovky. Dohodnime sa, že na vstupe je logická hodnota rovná 1 práve vtedy, keď je spínač zopnutý alebo tlačidlo stlačené. Podobne žiarovka svieti práve vtedy, keď je na príslušnom výstupe logická hodnota 1.
Úloha 1. V obvode na predchádzajúcom obrázku sú pred vstupmi A, B a C spínače a na výstupe je zapojená žiarovka. Ak spínač C nie je zopnutý, v akej polohe musia byť spínače A a B, aby žiarovka svietila?
Riešenie. Označme \(p(\mathrm{X})\) pravdivostnú hodnotu výroku \(\mathrm{X}\). Zo zadania vieme, že \(p(\mathrm{C})=0\), a pýtame sa na hodnoty \(p(\mathrm{A})\) a \(p(\mathrm{B})\) také, že \(p\left[ \left(\mathrm{C}\wedge \left(\mathrm{A}\vee\mathrm{B}\right)\right)\vee \left( \neg\left(\mathrm{A}\vee\mathrm{B}\right)\right) \right]=1\). Úlohu vyriešíme úvahou.
Ak platí, že \(p(\mathrm{C})=0\), potom nutne aj \(p(\mathrm{C}\wedge \left(\mathrm{A}\vee\mathrm{B}\right))=0\). Preto musí byť pravdivý výrok \(\neg ( \mathrm{A}\vee \mathrm{B})\), a teda \(p(\mathrm{A}\vee \mathrm{B})=0\). To je však možné vtedy a len vtedy, ak sú výroky \(\mathrm{A}\) aj \(\mathrm{B}\) nepravdivé. Ani jeden spínač teda nesmie byť zopnutý.
Úloha 2. Je daný logický obvod na obrázku nižšie, na ktorého vstupoch A, B a C sú spínače a na ktorého výstupe Z je zapojená žiarovka. Ktoré spínače musíme zopnúť, aby sa žiarovka rozsvietila? Nájdite všetky riešenia úlohy. Ak sa vodiče v diagrame krížia bez znázorneného uzla, považujú sa za neprepojené.
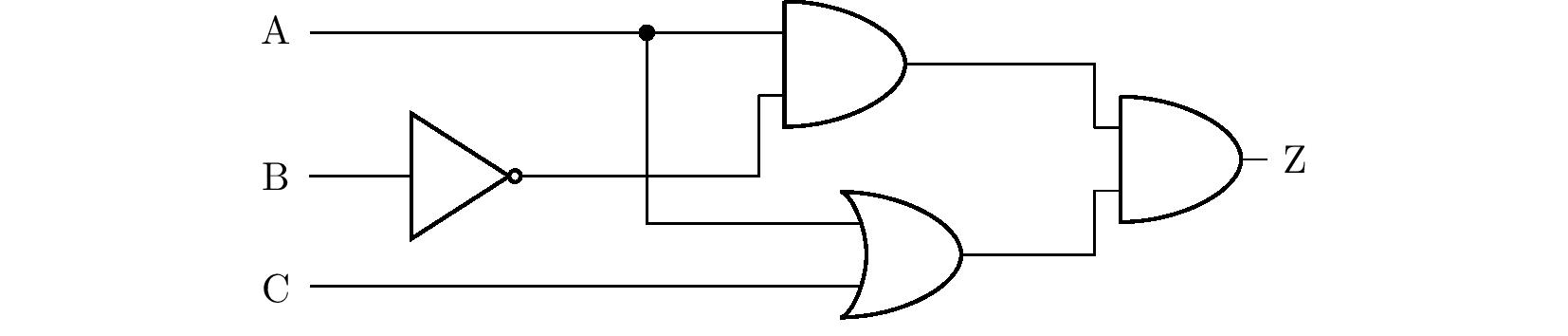
Riešenie. Úlohu budeme riešiť použitím tabuľky pravdivostných hodnôt. Na základe diagramu zo zadania najskôr odvodíme výrok zložený z výrokov \(\mathrm{A}\), \(\mathrm{B}\) a \(\mathrm{C}\), ktorý bude ekvivalentný výroku \(\mathrm{Z}\), pozri obrázok.
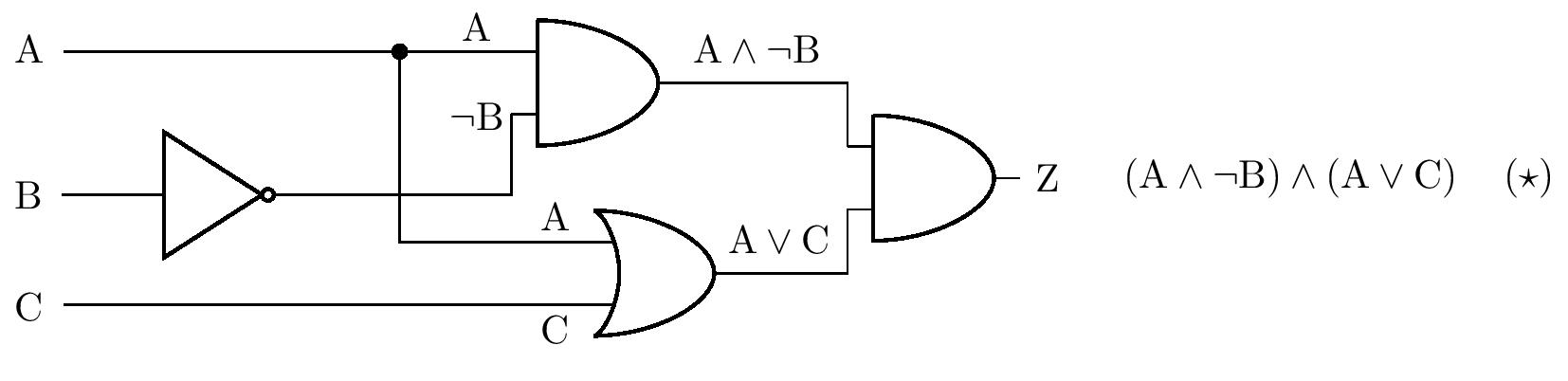
Pre zložený výrok \(\left( \star \right)\) teraz vytvoríme tabuľku pravdivostných hodnôt.
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{C}\) | \(\mathrm{A}\wedge\neg\mathrm{B}\) | \(\mathrm{A}\vee\mathrm{C}\) | \(\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \wedge \left( \mathrm{A}\vee\mathrm{C} \right)\) |
|---|---|---|---|---|---|
| \(1\) | \(1\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(1\) | \(1\) | \(0\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(1\) | \(0\) | \(1\) | \(\quad1\) | \(\quad1\) | \(\qquad\qquad1\) |
| \(1\) | \(0\) | \(0\) | \(\quad1\) | \(\quad1\) | \(\qquad\qquad1\) |
| \(0\) | \(1\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(0\) | \(1\) | \(0\) | \(\quad0\) | \(\quad0\) | \(\qquad\qquad0\) |
| \(0\) | \(0\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(0\) | \(0\) | \(0\) | \(\quad0\) | \(\quad0\) | \(\qquad\qquad0\) |
Z tabuľky vyplýva, že žiarovka bude svietiť práve vtedy, keď bude zopnutý spínač A a zároveň nebude zopnutý spínač B. Na zopnutí spínača C pritom nezáleží. Úlohu možno riešiť aj ekvivalentnými úpravami výroku \(\left(\star \right)\). Najprv použijeme distributívny zákon, následne tzv. zákon idempotencie \(\mathrm{A}\wedge \mathrm{A}\Leftrightarrow \mathrm{A}\):
\[ \begin{alignat*}{3} &&&\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \wedge \left( \mathrm{A}\vee\mathrm{C} \right) &&\quad\Leftrightarrow\\ &\Leftrightarrow\quad &&\left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{A}\right) \vee \left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{C}\right) &&\quad\Leftrightarrow\\ &\Leftrightarrow\quad &&\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \vee \left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{C}\right). && \tag{$\star\star$} \end{alignat*} \]
Zložený výrok \(\left( \star\star \right)\) je však pravdivý práve vtedy, keď je pravdivá konjunkcia \(\mathrm{A}\wedge\neg\mathrm{B}\), teda keď je \(\mathrm{A}\) pravdivý výrok a \(\mathrm{B}\) nepravdivý výrok. Z toho vyplýva o polohe spínačov rovnaký záver, ktorý sme učinili pomocou tabuľky.
Úloha 3. Navrhite logický obvod, ktorý v prípade poruchy niektorého z dvoch vodných čerpadiel (príp. oboch) rozsvieti výstražnú žiarovku na výstupe obvodu. Pokiaľ čerpadlo funguje, vysiela signál zodpovedajúci logickej jednotke na jeden z dvoch vstupov obvodu.
Riešenie. Označme \(\mathrm{A}\) a \(\mathrm{B}\) výroky predstavujúce stav prvého a druhého čerpadla. Hľadáme výrok \(\mathrm{Z}\) zložený z \(\mathrm{A}\) a \(\mathrm{B}\), ktorého tabuľku pravdivostných hodnôt poznáme:
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{Z}\) |
|---|---|---|
| \(1\) | \(1\) | \(0\) |
| \(1\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(1\) |
Z tabuľky vidíme, že ekvivalentným výrokom je napr. \(\neg\left( \mathrm{A} \wedge \mathrm{B}\right)\), ktorému zodpovedá diagram výsledného obvodu na obrázku:
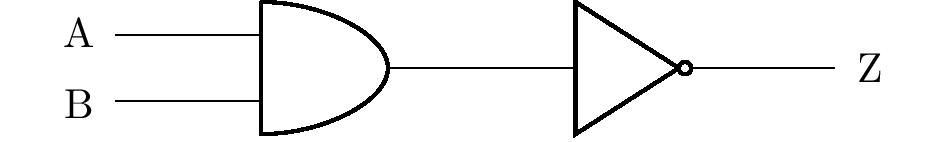
Úloha má viac riešení. Napríklad použitím de Morganovho pravidla dostávame z predchádzajúceho výsledku ekvivalentný výrok \(\neg\mathrm{A}\vee\neg\mathrm{B}\). Tomuto výroku by zodpovedal iný, ale tiež správny obvod (diagram).
Úloha 4. Modifikujte výstražné zariadenie z predchádzajúcej úlohy. Na dvoch výstupoch bude teraz zapojené červené a zelené svetlo. Ak fungujú obe čerpadlá, svieti zelené svetlo a červené je zhasnuté. Pri poruche jedného z čerpadiel sa navyše rozsvieti aj červené svetlo a pri poruche oboch čerpadiel bude svietiť iba červené svetlo. Navrhite zodpovedajúci logický obvod.
Riešenie. Podobne ako v predchádzajúcej úlohe označme \(\mathrm{A}\) a \(\mathrm{B}\) výroky vyjadrujúce stav prvého a druhého čerpadla. Takto dostaneme tabuľku pravdivostných hodnôt neznámych zložených výrokov \(\mathrm{Č}\) (červené svetlo) a \(\mathrm{Z}\) (zelené svetlo):
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{Č}\) | \(\mathrm{Z}\) |
|---|---|---|---|
| \(1\) | \(1\) | \(0\) | \(1\) |
| \(1\) | \(0\) | \(1\) | \(1\) |
| \(0\) | \(1\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(1\) | \(0\) |
Je vidieť, že stĺpec pre výrok \(\mathrm{Č}\) je totožný s výrokom \(\mathrm{Z}\) v predchádzajúcej úlohe (a teda môžeme prevziať jej riešenie), a stĺpec pre výrok \(\mathrm{Z}\) zodpovedá disjunkcii \(\mathrm{A}\vee \mathrm{B}\). Využitím uzlov a rozvetvením obvodu tak môžeme zakresliť diagram zodpovedajúceho logického obvodu:
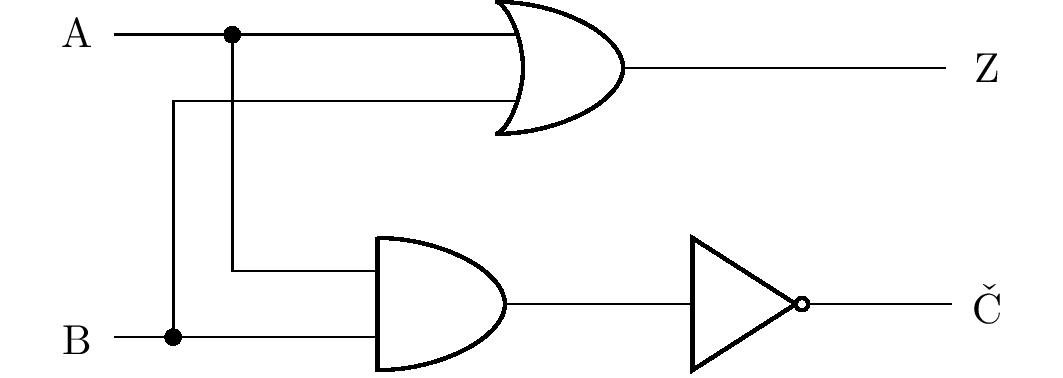
Podobne ako predchádzajúca úloha má aj táto viac riešení, ktorých správnosť je možné overiť vždy pomocou tabuľky pravdivostných hodnôt. Bližšie sa však vyjadríme ešte k jednému riešeniu. Žiakov môže napadnúť, že namiesto člena OR je možné vodiče spojiť jednoduchým uzlom, ako je znázornené na obrázku:
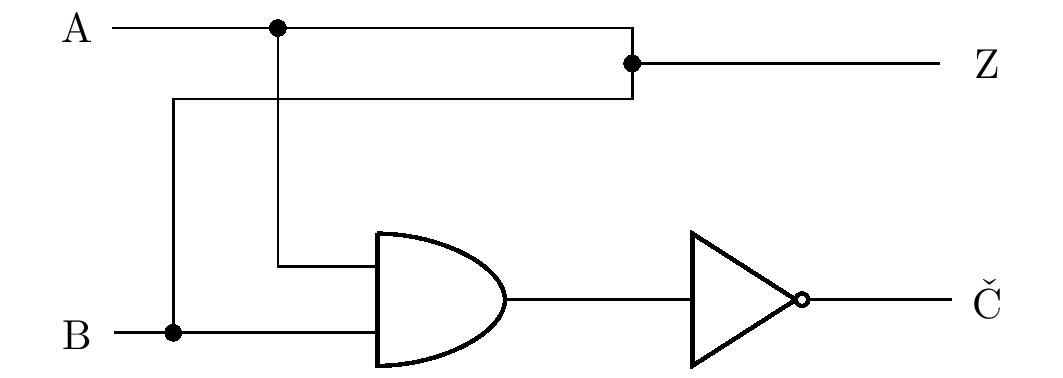
Ak platí, že na vstupe \(\mathrm{A}\) alebo \(\mathrm{B}\) (prípadne na oboch) je hodnota \(1\), nemusí táto hodnota automaticky prechádzať aj na výstup \(\mathrm{Z}\). V skutočnosti to tak vôbec neplatí. V úvode sme si stanovili, že logická hodnota \(1\) sa reprezentuje vysokou úrovňou napätia a hodnota \(0\) sa reprezentuje nízkou úrovňou napätia. Ak je teda na vstupe \(\mathrm{A}\) vysoké napätie a na vstupe \(\mathrm{B}\) nízke napätie, v obvode dôjde ku skratu, pretože vodič spája uzly s rôznymi úrovňami napätia. Preto vo všeobecnosti v logických obvodoch nemôžeme spájať výstupy rôznych členov priamo do jedného uzla.
Úloha 5. Navrhite logický obvod s dvoma vstupmi a jedným výstupom, ktorý simuluje operáciu logickej ekvivalencie.
Riešenie. Aby sme mohli obvod zostrojiť, potrebujeme nájsť ku ekvivalencii \(\mathrm{A}\Leftrightarrow\mathrm{B}\) zložený výrok s rovnakou pravdivostnou tabuľkou, ktorý obsahuje iba konjunkcie, disjunkcie alebo negácie. Z definície pre ekvivalenciu vyplýva, že je pravdivá práve vtedy, keď sú výroky \(\mathrm{A}\) a \(\mathrm{B}\) oba pravdivé alebo oba nepravdivé. To znamená, že je pravdivá práve vtedy, keď je pravdivá konjunkcia \(\mathrm{A}\wedge\mathrm{B}\) alebo je pravdivá konjunkcia \(\neg\mathrm{A}\wedge\neg\mathrm{B}\). Tak dostávame ekvivalenciu \[
\left( \mathrm{A}\Leftrightarrow\mathrm{B} \right)
\quad \Leftrightarrow \quad
\left( \mathrm{A}\wedge\mathrm{B} \right) \vee \left( \neg\mathrm{A}\wedge\neg\mathrm{B} \right),
\] ktorej pravá strana je výrok obsahujúci iba konjunkcie, disjunkcie a negácie. Môžeme preto zostaviť zodpovedajúci diagram: 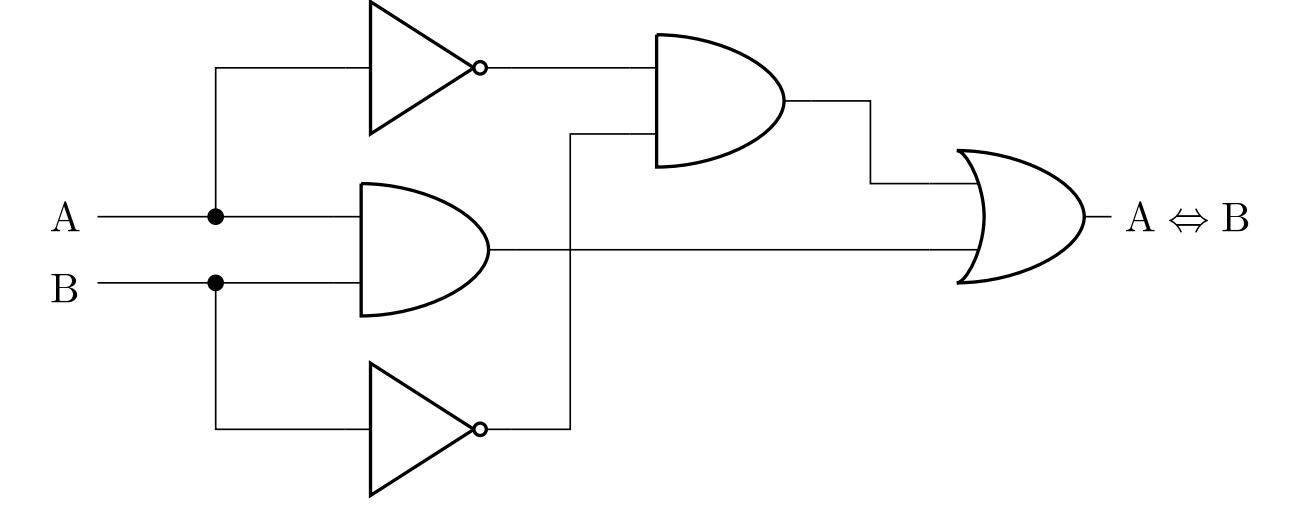
Jedno z ďalších možných riešení môžeme dostať využitím de Morganovych pravidiel a ekvivalentnou úpravou predchádzajúceho výsledku na výrok \(\left( \mathrm{A}\wedge\mathrm{B} \right) \vee \neg \left( \mathrm{A}\vee\mathrm{B} \right)\). Technickou výhodou tohto tvaru je menší počet potrebných logických členov pri realizácii obvodu.
Úloha 6. Kávový automat po stlačení príslušného tlačidla vie pripraviť tri typy nápojov: lungo, macchiato a kakao. Nápoje sa pripravujú miešaním štyroch ingrediencií (horúcej vody, mlieka, kávového a kakaového koncentrátu), kde každá ingrediencia má svoju trysku. Navrhite logický obvod s tromi vstupmi (pre každý nápoj jeden) a štyrmi výstupmi (pre ventil každej trysky jeden), ak sa lungo pripravuje z vody a kávového koncentrátu, macchiato z vody, mlieka a kávového koncentrátu a kakao z vody a kakaového koncentrátu. Pre jednoduchosť predpokladajme, že nikoho nenapadne stlačiť viac tlačidiel naraz, teda sa týmito prípadmi nemusíte zaoberať. Ingrediencia je do poháriku uvoľnená práve vtedy, keď je na príslušnom výstupe logická jednotka.
Riešenie. Označme \(\mathrm{C}\) (kakao, angl. cocoa), \(\mathrm{L}\) (lungo) a \(\mathrm{M}\) (macchiato) výroky predstavujúce stav stlačenia príslušného tlačidla a ďalej označme \(\mathrm{COC}\) (kakaový koncentrát, angl. cocoa concentrate), \(\mathrm{WA}\) (voda, angl. water), \(\mathrm{COF}\) (kávový koncentrát, angl. coffee concentrate) a \(\mathrm{ML}\) (mlieko, angl. milk) výroky predstavujúce stav otvorenia príslušnej trysky. Z informácií v zadaní potom zostavme tabuľku pravdivostných hodnôt:
| \(\mathrm{C}\) | \(\mathrm{L}\) | \(\mathrm{M}\) | \(\mathrm{COC}\) | \(\mathrm{WA}\) | \(\mathrm{COF}\) | \(\mathrm{ML}\) |
|---|---|---|---|---|---|---|
| \(1\) | \(0\) | \(0\) | \(1\) | \(1\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(0\) | \(0\) | \(1\) | \(1\) | \(0\) |
| \(0\) | \(0\) | \(1\) | \(0\) | \(1\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) |
Riadky, pre ktoré je v prvých troch stĺpcoch viac ako jedna jednotka, neberieme do úvahy, pretože je možné stlačiť vždy len jedno tlačidlo.
Z tabuľky plynie, že ekvivalentnou dvojicou výrokov je \(\mathrm{COC}\) a \(\mathrm{C}\) a ďalšou ekvivalentnou dvojicou sú výroky \(\mathrm{ML}\) a \(\mathrm{M}\). Výrok \(\mathrm{COF}\) je pravdivý práve vtedy, keď je pravdivý niektorý z výrokov \(\mathrm{L}\) alebo \(\mathrm{M}\), teda je ekvivalentný s disjunkciou \(\mathrm{L}\vee\mathrm{M}\). A nakoniec výrok \(\mathrm{WA}\) je pravdivý práve vtedy, keď je niektorý z trojice výrokov \(\mathrm{C}\), \(\mathrm{L}\), \(\mathrm{M}\) pravdivý, teda je \(\mathrm{WA}\) ekvivalentný s disjunkciou \(\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}\).
Na nasledujúcom obrázku je znázornený diagram príslušného obvodu - disjunkcia \(\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}\) je v ňom pritom realizovaná vnorením dvoch členov OR, t. j. ako \(\mathrm{C}\vee\left( \mathrm{L}\vee\mathrm{M}\right)\).
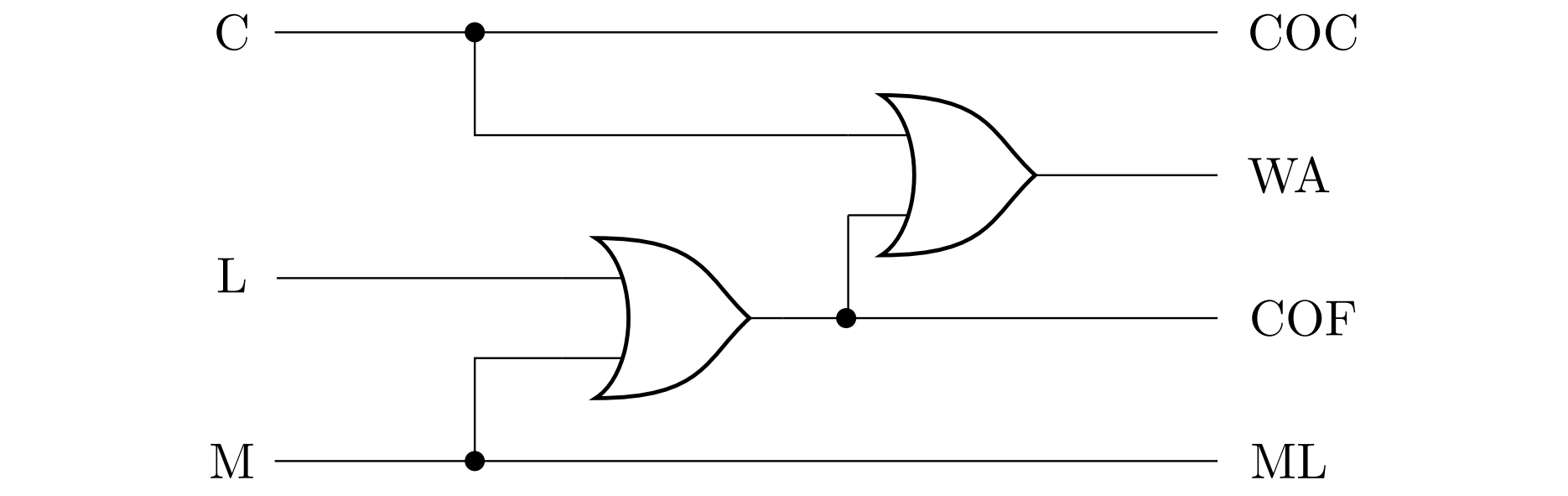
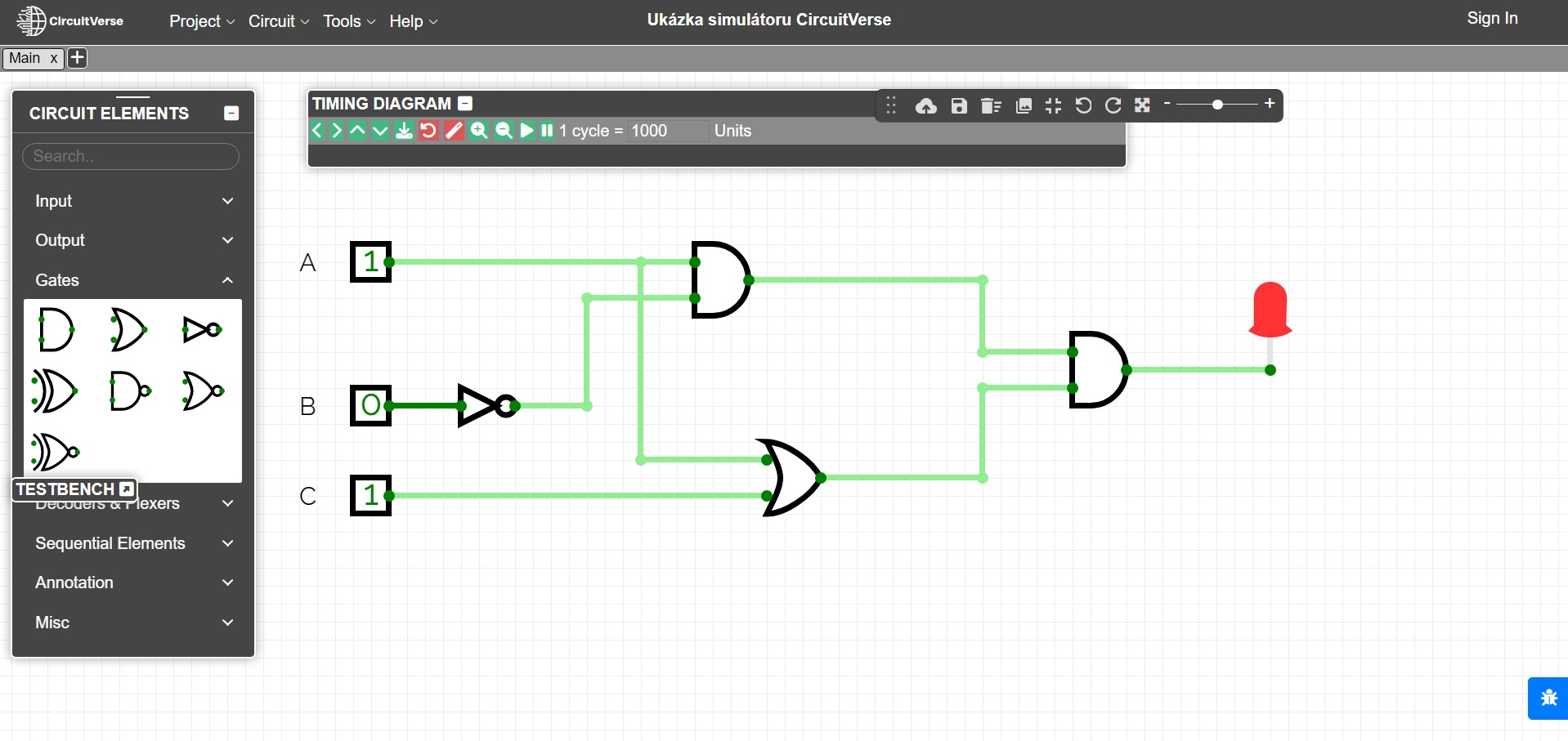
Všetky uvedené úlohy je možné názorne ilustrovať na rôznych simulátoroch logických obvodov, napr. online simulátore CircuitVerse. Na poslednom obrázku je v tomto simulátore modelovaný obvod z Úlohy 2. K ilustrácii je tiež možné využiť špecializované elektronické stavebnice.
Literatúra
- Perrin J. P., Denouette M., Daclin E. Logické systémy, díl I. Kombinační logické obvody. Úvod do sekvenčních obvodů. Praha: SNTL. 1972
- Online simulátor CircuitVerse, https://circuitverse.org/simulator