Circuitos lógicos
 35 min.,
35 min.,  2/3
2/3 ¿Qué hechizo puede encender la luz adecuada en un ascensor repleto, pulsar un botón en una máquina expendedora para hacer un refresco de naranja, apagar las luces del pasillo de una casa después de unos minutos o mover un personaje en la pantalla de un ordenador? De estas y otras muchas actividades de la vida real se encargan los circuitos lógicos que exploraremos con más detalle en la próxima serie de problemas.
Los circuitos lógicos constan de los llamados miembros lógicos, que implementan operaciones lógicas. En los problemas trabajaremos sólo con tres miembros lógicos básicos NOT (negación), AND (conjunción) y OR (disyunción). La figura muestra sus símbolos respectivos (según la norma americana ANSI/MIL) en los circuitos lógicos. Están orientados de forma que la dirección de entrada es por la izquierda. Las entradas se entienden como enunciados, mientras que las salidas son enunciados compuestos.

Los valores de verdad se realizan mediante tensión circuitos lógicos, una tensión baja indica un valor de verdad de 0, un nivel de tensión alto indica un valor de 1. Si, por ejemplo, el componente AND tiene un nivel de tensión bajo en la entrada A y un nivel de tensión alto en la entrada B, la salida es un nivel de tensión bajo. Los valores específicos de los niveles varían según el uso específico del circuito. Por ejemplo, un nivel bajo de aproximadamente 0V y un nivel alto de aproximadamente 5V son comunes.
En la siguiente figura vemos una representación de un circuito lógico más complejo. Para mayor claridad, la figura indica también la composición secuencial de los enunciados, que corresponde a las entradas o salidas de cada miembro. El punto negro indica el nudo en el que el circuito lógico se bifurca. Así, la salida de un miembro puede ser conectada a varias entradas simultáneamente.
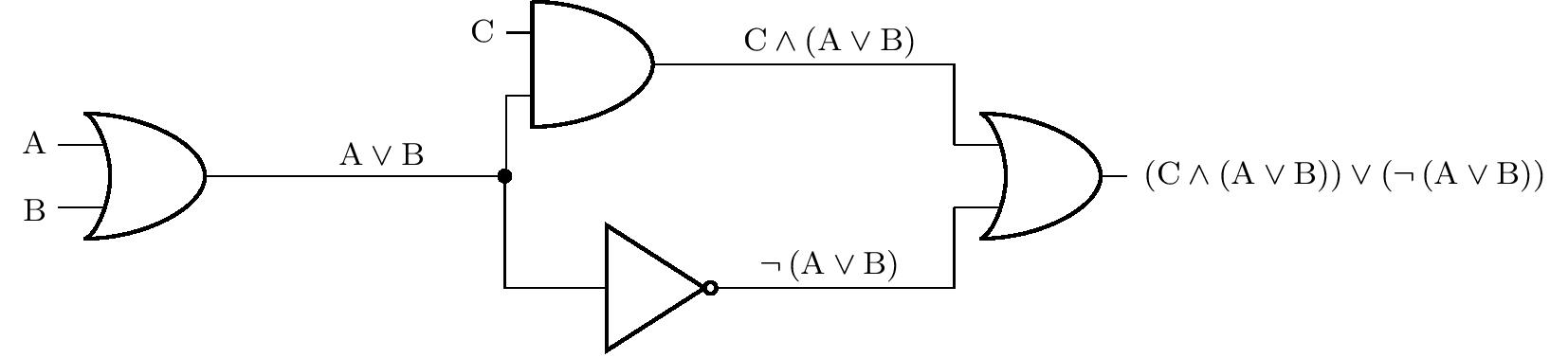
En los siguientes problemas, se pueden incluir interruptores o botones antes de las entradas, y bombillas después de las salidas del circuito lógico. Convengamos en que el valor lógico en la entrada es igual a 1 justo cuando el interruptor está encendido o el botón está pulsado. Del mismo modo, una bombilla se enciende precisamente cuando el valor lógico de 1 está en la salida correspondiente.
Tarea 1. En el circuito mostrado en la imagen anterior hay interruptores ante las entradas A, B y C y una bombilla está conectada a la salida. Si el interruptor C no está encendido, ¿en qué posición deben estar los interruptores A y B para que la bombilla se encienda?
Solución. Sea \(p(\mathrm{X})\) el valor de verdad del enunciado \(\mathrm{X}\). Del enunciado del problema sabemos que \(p(\mathrm{C})=0\), y preguntamos por los valores de \(p(\mathrm{A})\) a \(p(\mathrm{B})\) tales que, \(p\left[ \left(\mathrm{C}\wedge \left(\mathrm{A}\vee\mathrm{B}\right)\right)\vee \left( \neg\left(\mathrm{A}\vee\mathrm{B}\right)\right) \right]=1\). Resolvemos el problema por razonamiento.
Si \(p(\mathrm{C})=0\), entonces necesariamente
\(p(\mathrm{C}\wedge \left(\mathrm{A}\vee\mathrm{B}\right))=0\). Por lo tanto la afirmación \(\neg ( \mathrm{A}\vee \mathrm{B})\), debe ser cierta, y por lo tanto \(p(\mathrm{A}\vee \mathrm{B})=0\). Sin embargo, esto es posible sólo si las afirmaciones \(\mathrm{A}\) i \(\mathrm{B}\) son ambas falsas. Por lo tanto, ninguno de los dos interruptores puede estar encendido.
Tarea 2. Se da el circuito lógico de la figura siguiente, cuyas entradas A, B y C son interruptores y cuya salida Z es una bombilla. ¿Qué interruptores deben estar encendidos para que se encienda la bombilla? Encuentra todas las soluciones al problema. Si los cables se cruzan en el diagrama sin que se muestre un nudo, se supone que en la realidad no hay contacto entre los cables.
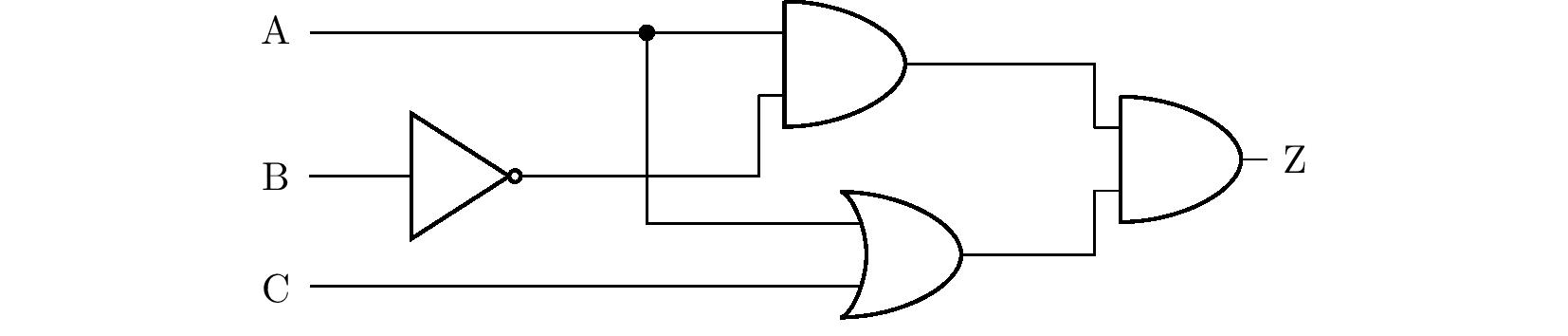
Solución. Resolveremos el problema utilizando la tabla de valores de verdad. A partir del diagrama de la tarea, derivamos primero un enunciado formado por los enunciados \(\mathrm{A}\), \(\mathrm{B}\) a \(\mathrm{C}\), que será equivalente al enunciado \(\mathrm{Z}\), ver figura.
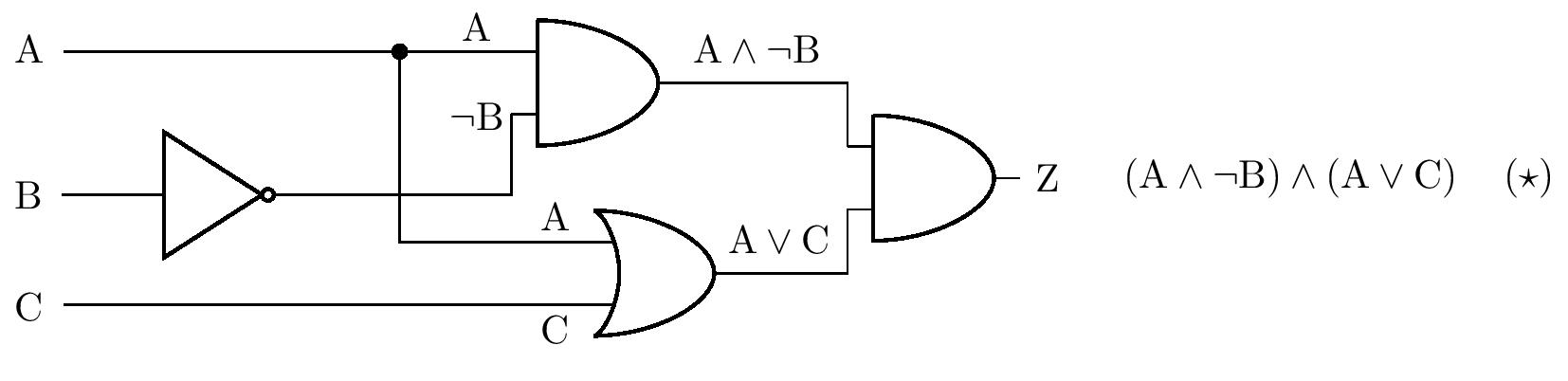
Para el enunciado compuesto \(\left( \star \right)\) creamos ahora una tabla de valores de verdad:
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{C}\) | \(\mathrm{A}\wedge\neg\mathrm{B}\) | \(\mathrm{A}\vee\mathrm{C}\) | \(\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \wedge \left( \mathrm{A}\vee\mathrm{C} \right)\) |
|---|---|---|---|---|---|
| \(1\) | \(1\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(1\) | \(1\) | \(0\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(1\) | \(0\) | \(1\) | \(\quad1\) | \(\quad1\) | \(\qquad\qquad1\) |
| \(1\) | \(0\) | \(0\) | \(\quad1\) | \(\quad1\) | \(\qquad\qquad1\) |
| \(0\) | \(1\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(0\) | \(1\) | \(0\) | \(\quad0\) | \(\quad0\) | \(\qquad\qquad0\) |
| \(0\) | \(0\) | \(1\) | \(\quad0\) | \(\quad1\) | \(\qquad\qquad0\) |
| \(0\) | \(0\) | \(0\) | \(\quad0\) | \(\quad0\) | \(\qquad\qquad0\) |
La tabla muestra que la bombilla estará encendida si el interruptor A está activado y el interruptor B. no está activado. El interruptor C es indiferente.
El problema también puede resolverse mediante modificaciones equivalentes del enunciado \(\left(\star \right)\). Primero usamos la ley distributiva, luego la llamada ley de idempotencia \(\mathrm{A}\wedge \mathrm{A}\Leftrightarrow \mathrm{A}\):
\[ \begin{alignat*}{3} &&&\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \wedge \left( \mathrm{A}\vee\mathrm{C} \right) &&\quad\Leftrightarrow\\ &\Leftrightarrow\quad &&\left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{A}\right) \vee \left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{C}\right) &&\quad\Leftrightarrow\\ &\Leftrightarrow\quad &&\left( \mathrm{A}\wedge\neg\mathrm{B}\right) \vee \left( \mathrm{A}\wedge\neg\mathrm{B}\wedge\mathrm{C}\right). && \tag{$\star\star$} \end{alignat*} \]
Sin embargo, el enunciado compuesto \(\left( \star\star \right)\) es verdadero sólo si la conjunción \(\mathrm{A}\wedge\neg\mathrm{B}\), es verdadera, es decir, si \(\mathrm{A}\) es un enunciado verdadero y \(\mathrm{B}\) es un enunciado falso. Esto implica la misma conclusión sobre la posición de los interruptores que hicimos utilizando la tabla.
Tarea 3. Diseñar un circuito lógico que, en caso de fallo de una de las dos bombas de agua (o de ambas), encienda una lámpara de aviso a la salida del circuito. Mientras la bomba está en funcionamiento, envía una señal correspondiente a la lógica una a una de las dos
entradas del circuito.
Solución. Señalemos \(\mathrm{A}\) y \(\mathrm{B}\) por los enunciados que representan el estado de la primera y segunda bombas. Buscamos el enunciado \(\mathrm{Z}\) formado por \(\mathrm{A}\) y \(\mathrm{B}\), cuya tabla de valor de verdad conocemos:
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{Z}\) |
|---|---|---|
| \(1\) | \(1\) | \(0\) |
| \(1\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(1\) |
De la tabla podemos ver que el enunciado equivalente es, por ejemplo, \(\neg\left( \mathrm{A} \wedge \mathrm{B}\right)\), que corresponde al diagrama del circuito resultante en la figura:
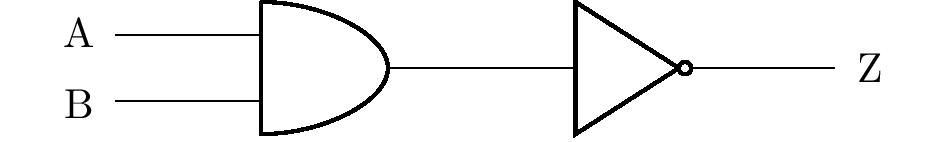
El problema tiene múltiples soluciones. Por ejemplo, utilizando la ley de Morgan, obtenemos el enunciado
equivalente \(\neg\mathrm{A}\vee\neg\mathrm{B}\). a partir del resultado anterior. Un circuito (diagrama) diferente, pero también correcto, correspondería a esta afirmación.
Tarea 4. Modificar el dispositivo de alerta de la tarea anterior. Las dos salidas tendrán ahora una luz roja y otra verde. Si las dos bombas funcionan, la luz verde estará encendida y la roja apagada. Además, si una bomba falla, la luz čroja también estará encendida y si ambas bombas fallan, sólo la luz roja estará encendida. Diseña un circuito lógico correspondiente.
Solución. De forma similar al problema anterior, señalemos \(\mathrm{A}\) a \(\mathrm{B}\) como enunciados que representan el estado de la primera y segunda bombas. Esto produce
una tabla de los valores de verdad de las afirmaciones compuestas desconocidas \(\mathrm{Č}\) (luz roja) a \(\mathrm{Z}\) (luz verde):
| \(\mathrm{A}\) | \(\mathrm{B}\) | \(\mathrm{Č}\) | \(\mathrm{Z}\) |
|---|---|---|---|
| \(1\) | \(1\) | \(0\) | \(1\) |
| \(1\) | \(0\) | \(1\) | \(1\) |
| \(0\) | \(1\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(1\) | \(0\) |
Se puede observar que la columna del enunciado \(\mathrm{Č}\) es idéntica al enunciado \(\mathrm{Z}\) del problema anterior (y por tanto podemos tomar su solución), y la columna del enuciado \(\mathrm{Z}\) corresponde a la disyunción \(\mathrm{A}\vee \mathrm{B}\). Así, utilizando los nodos y ramificando el circuito, podemos dibujar un diagrama del circuito lógico correspondiente:
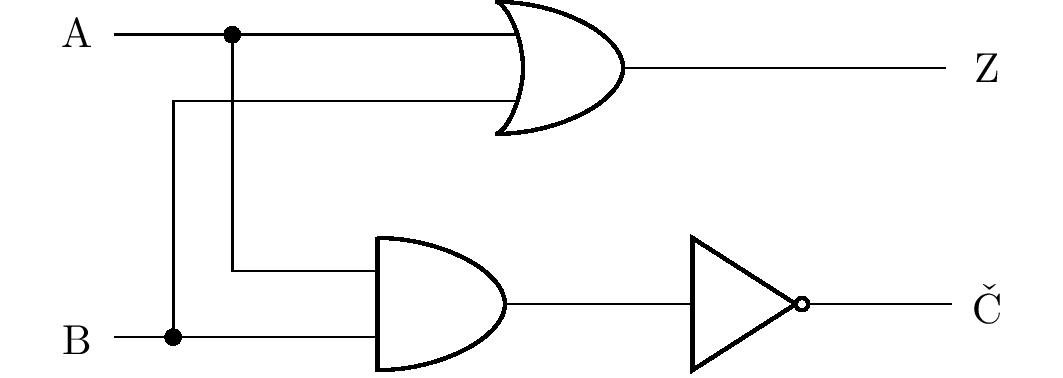
Al igual que el problema anterior, éste tiene múltiples soluciones, cuya corrección puede verificarse siempre utilizando la tabla de valores de verdad . Sin embargo, lo comentaremos más detenidamente en una solución.
Los alumnos pueden pensar que, en lugar de un término OR, los cables pueden conectarse mediante un simple nudo, como se muestra en la figura:
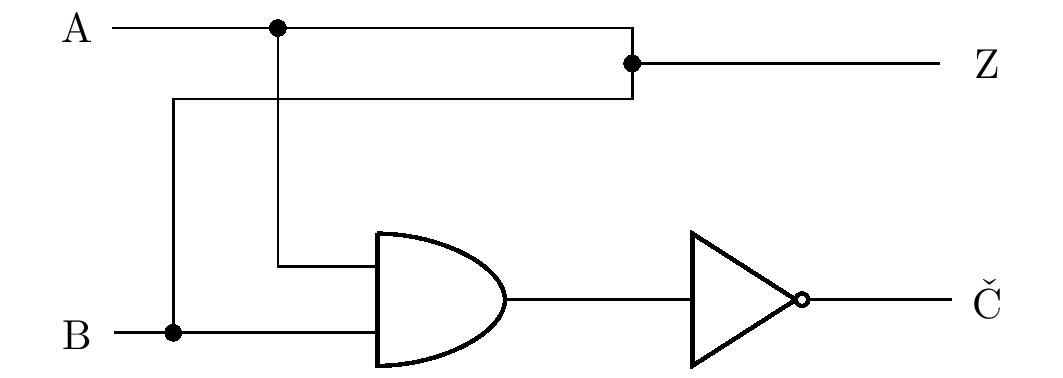
Si se encuentra \(\mathrm{A}\) o \(\mathrm{B}\) (o en ambos) el valor \(1\), ¿puede este valor fluir libremente a través de la salida de \(\mathrm{Z}\,\)? La realidad es que no lo hace. En el párrafo introductorio, señalamos que el valor de verdad \(1\) se realiza por el alto nivel de la tensión y el valor \(0\) por su bajo nivel. Así, por ejemplo, si la entrada de \(\mathrm{A}\) es alta y la entrada de \(\mathrm{B}\) nízké napětí, es baja, se producirá un cortocircuito, porque los puntos con tensiones diferentes están conectados por un conductor. Por lo tanto, en general, no podemos conectar salidas de diferentes miembros con nudos en circuitos lógicos.
Tarea 5. Diseñar un circuito lógico con dos entradas y una salida que simule una operación de equivalencia lógica.
Solución. Para construir el circuito, necesitamos encontrar una equivalencia \(\mathrm{A}\Leftrightarrow\mathrm{B}\) del enunciado compuesto con la misma tabla de verdad de valores que contenga sólo conjunciones, disyunciones o negaciones. La definición de equivalencia implica que es verdadera precisamente si los enunciados \(\mathrm{A}\) y \(\mathrm{B}\) son ambos verdaderos o ambos falsos. Esto significa que es verdadera precisamente si la
conjunción \(\mathrm{A}\wedge\mathrm{B}\) o la conjunción \(\neg\mathrm{A}\wedge\neg\mathrm{B}\) son verdaderas. Entonces obtenemos la equivalencia \[
\left( \mathrm{A}\Leftrightarrow\mathrm{B} \right)
\quad \Leftrightarrow \quad
\left( \mathrm{A}\wedge\mathrm{B} \right) \vee \left( \neg\mathrm{A}\wedge\neg\mathrm{B} \right),
\] cuyo lado derecho es un enunciado que sólo contiene conjunciones, disyunciones y negaciones. Por lo tanto, podemos construir el diagrama correspondiente:
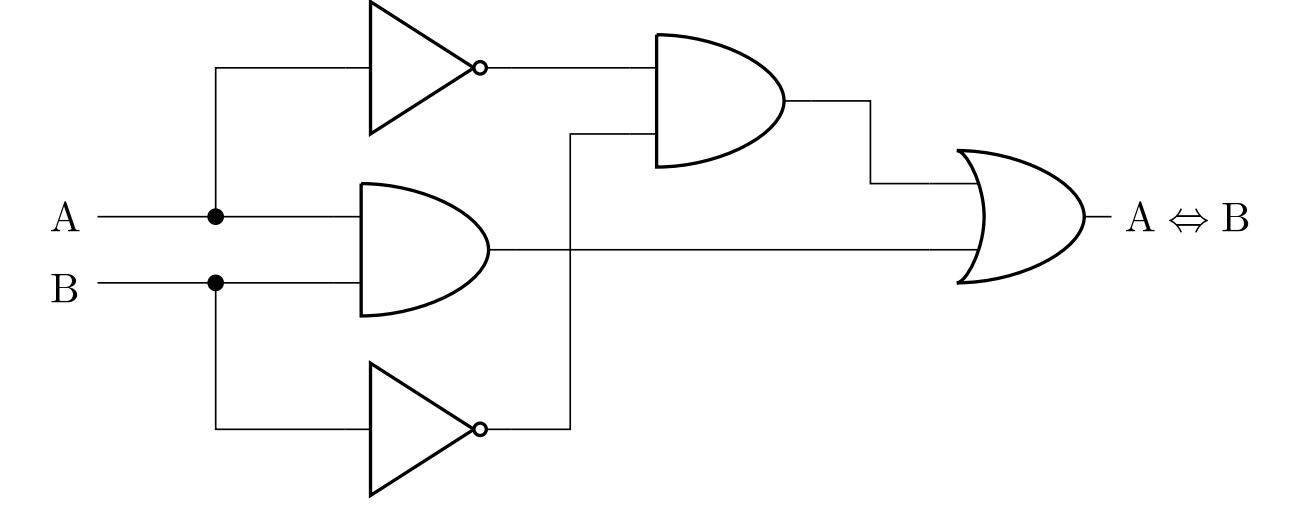
Otra posible solución puede obtenerse utilizando las leyes de Morgan y modificando equivalentemente el resultado anterior por el enunciado \(\left( \mathrm{A}\wedge\mathrm{B} \right) \vee \neg \left( \mathrm{A}\vee\mathrm{B} \right)\). La ventaja técnica de esta forma es el menor número de componentes lógicos necesarios en la implementación del circuito.
Tarea 6. La cafetera puede preparar tres tipos de bebidas: lungo, macchiato y cacao pulsando el botón correspondiente. Las bebidas se preparan mezclando cuatro ingredientes (agua caliente, leche, café y concentrado de cacao), donde cada ingrediente tiene su propia boquilla. Diseñe un circuito lógico con tres entradas (una para cada bebida) y cuatro salidas (una para cada válvula de boquilla) teniendo en cuenta que el lungo se prepara a partir de agua y concentrado de café, el macchiato a partir de agua, leche y concentrado de café, y el cacao a partir de agua y concentrado de cacao.
Para simplificar, vamos a suponer que a nadie se le ocurre pulsar varios botones a la vez, por lo que no hay que lidiar con estos casos. Un ingrediente se libera en el vaso justo cuando en la salida correspondiente hay, lógicamente, uno.
Solución. Señalemos \(\mathrm{C}\) (kakao, angl. cocoa), \(\mathrm{L}\) (lungo) a \(\mathrm{M}\) (macchiato) por los enunciados que representan el estado de pulsar el botón correspondiente y además por \(\mathrm{COC}\) (concentrado de cacao, en inglés, cocoa concentrate), \(\mathrm{WA}\) (voda, angl. water), \(\mathrm{COF}\) (concentrado de café, en inglés, coffee concentrate) a \(\mathrm{ML}\) (leche, en inglés, milk) enunciados que representan el estado de abrir la boquilla respectiva. A partir de la información de la instrucción, construyamos entonces una tabla de verdad de valores:
| \(\mathrm{C}\) | \(\mathrm{L}\) | \(\mathrm{M}\) | \(\mathrm{COC}\) | \(\mathrm{WA}\) | \(\mathrm{COF}\) | \(\mathrm{ML}\) |
|---|---|---|---|---|---|---|
| \(1\) | \(0\) | \(0\) | \(1\) | \(1\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(0\) | \(0\) | \(1\) | \(1\) | \(0\) |
| \(0\) | \(0\) | \(1\) | \(0\) | \(1\) | \(1\) | \(1\) |
| \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) |
Las filas con más de un 1 en las tres primeras columnas no se tienen en cuenta porque sólo se puede pulsar un botón a la vez.
La tabla muestra que el par equivalente de enunciados es \(\mathrm{COC}\) a \(\mathrm{C}\) y el otro par equivalente es \(\mathrm{ML}\) a \(\mathrm{M}\). El enunciado \(\mathrm{COF}\) es verdadero sólo si es verdadero cualquiera de los enunciados \(\mathrm{L}\) nebo \(\mathrm{M}\), por lo que es equivalente a la disyunción \(\mathrm{L}\vee\mathrm{M}\). Por último, el enunciado \(\mathrm{WA}\) es verdadero sólo si, cualquiera de la tripleta de enunciados \(\mathrm{C}\), \(\mathrm{L}\), \(\mathrm{M}\) es verdadero, es decir \(\mathrm{WA}\) es equivalente a la disyunción \(\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}\).
La siguiente figura muestra un diagrama del circuito correspondiente: la disyunción \(\mathrm{C}\vee\mathrm{L}\vee\mathrm{M}\) se realiza empleando dos términos OR, es decir, como \(\mathrm{C}\vee\left( \mathrm{L}\vee\mathrm{M}\right)\).
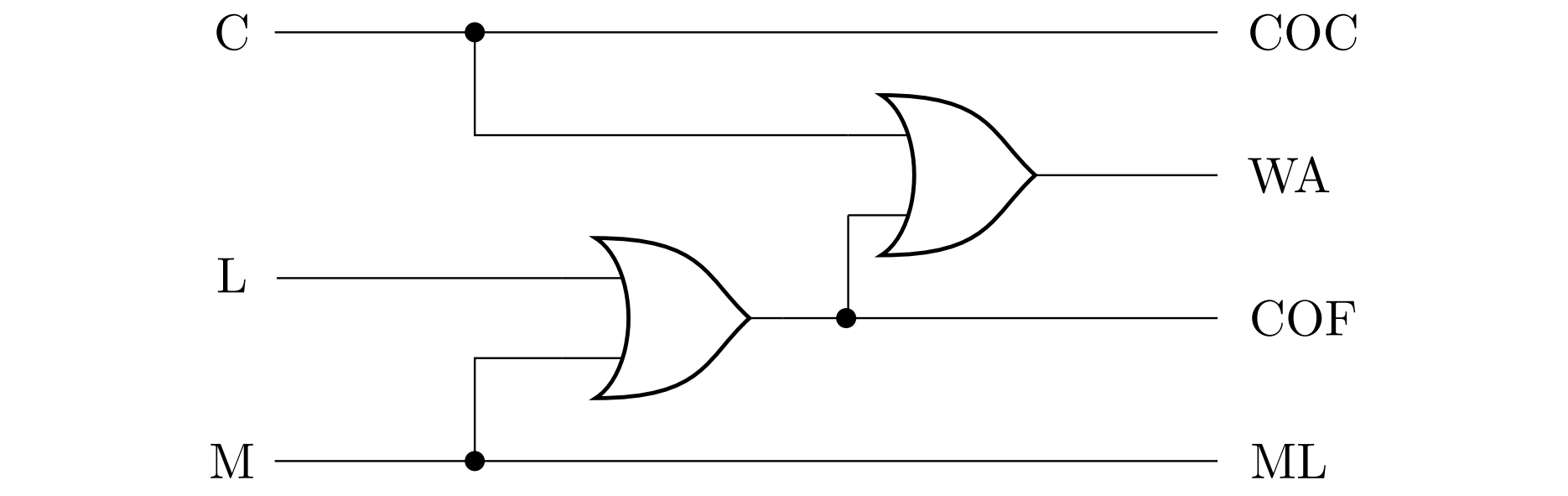
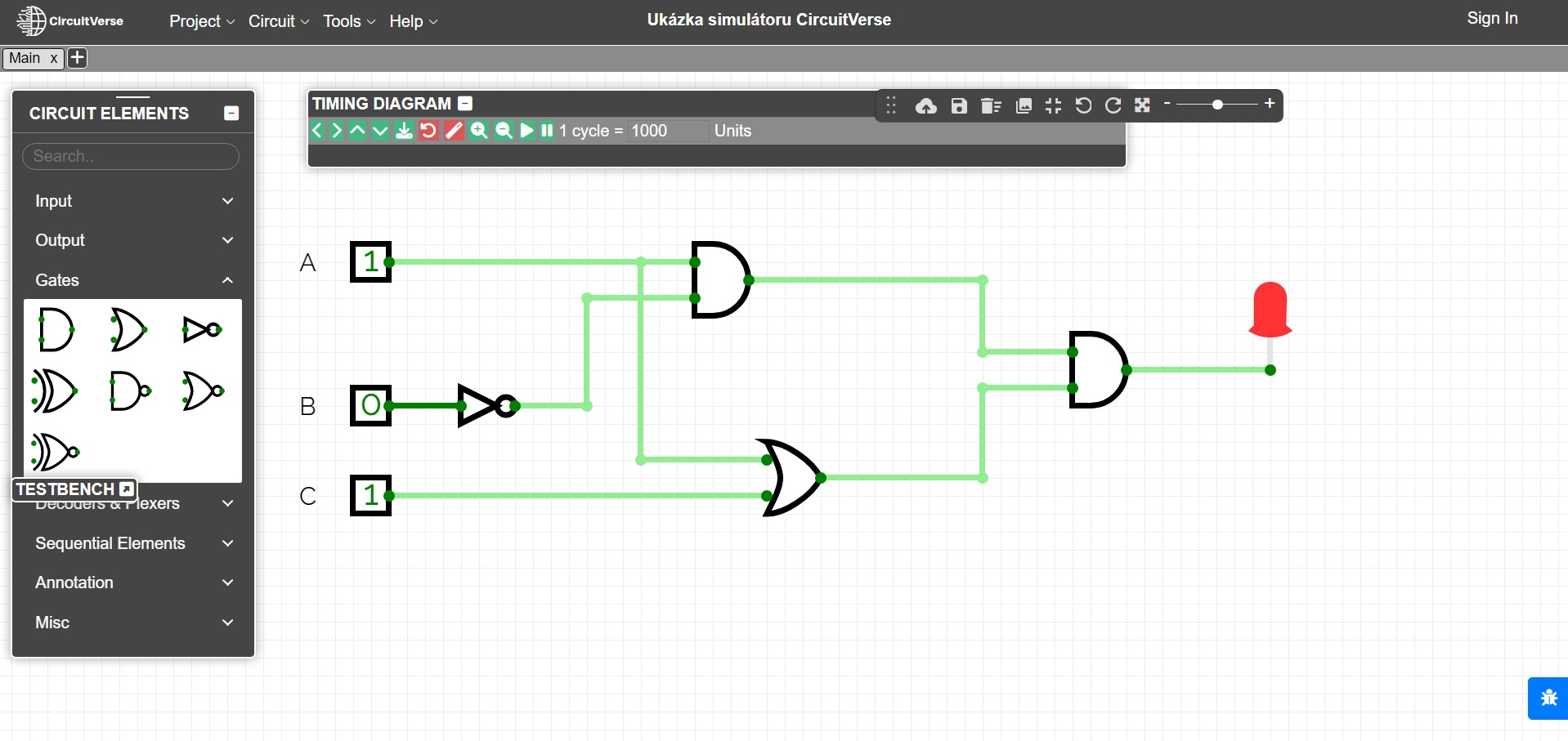
Todas estas tareas pueden ilustrarse en diversos simuladores de circuitos lógicos, como el simulador en línea CircuitVerse. En la última figura, el circuito del problema 2 se modela en este simulador.
Bibliografía
- Perrin J. P., Denouette M., Daclin E. Logické systémy, díl I. Kombinační logické obvody. Úvod do sekvenčních obvodů. Praha: SNTL. 1972
- Online simulátor CircuitVerse, https://circuitverse.org/simulator