Parabolická anténa
 20 min.,
20 min.,  2/3
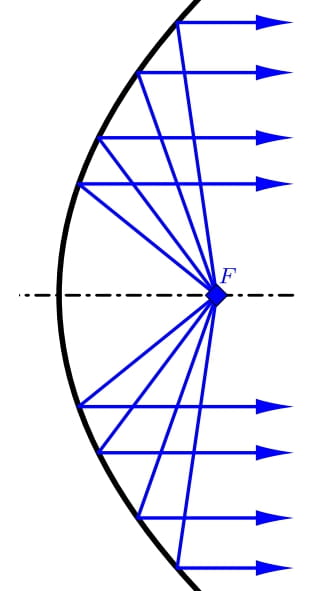
2/3 Kvalitná anténa je jedným z najdôležitejších prvkov každého radaru. Jedným typom antény je takzvaná parabolická anténa. Táto anténa má tvar rotačného paraboloidu (to znamená, že vznikla rotáciou časti paraboly okolo jej osi) a používa sa nielen na rádiolokáciu, ale aj napríklad na príjem satelitného televízneho vysielania. Parabolický tvar prijímacej antény zabezpečuje, že prichádzajúce signály z určitého smeru sa po odraze od antény sústredia v jednom bode. Konkrétne v ohnisku paraboly, ktorej rotáciou anténa vznikla. Prijímač antény sa preto nachádza v tomto bode. Na druhej strane, ak sa výstup vysokofrekvenčného generátora (vysielač) nachádza v ohnisku, anténa funguje ako vysielač. Po odraze od paraboloidu sa energia z vysielača sústreďuje do úzkeho lúča mikrovĺn s rovnobežnými lúčmi.
Osovým rezom antény je časť paraboly. Charakterizuje sa dvoma parametrami. Sú to priemer \(d\) antény a hĺbka \(h\) antény, pozri obrázok. Tieto dva parametre určujú polohu ohniska \(F\). Vzdialenosť ohniska od vrcholu paraboly označujeme \(f\). Poslednou dôležitou charakteristikou antény je jej uhol otvorenia, ktorý vyjadruje, pod akým uhlom vidíme okraje časti paraboly z ohniska. Jeho hodnotu označujeme \(2\varphi\).
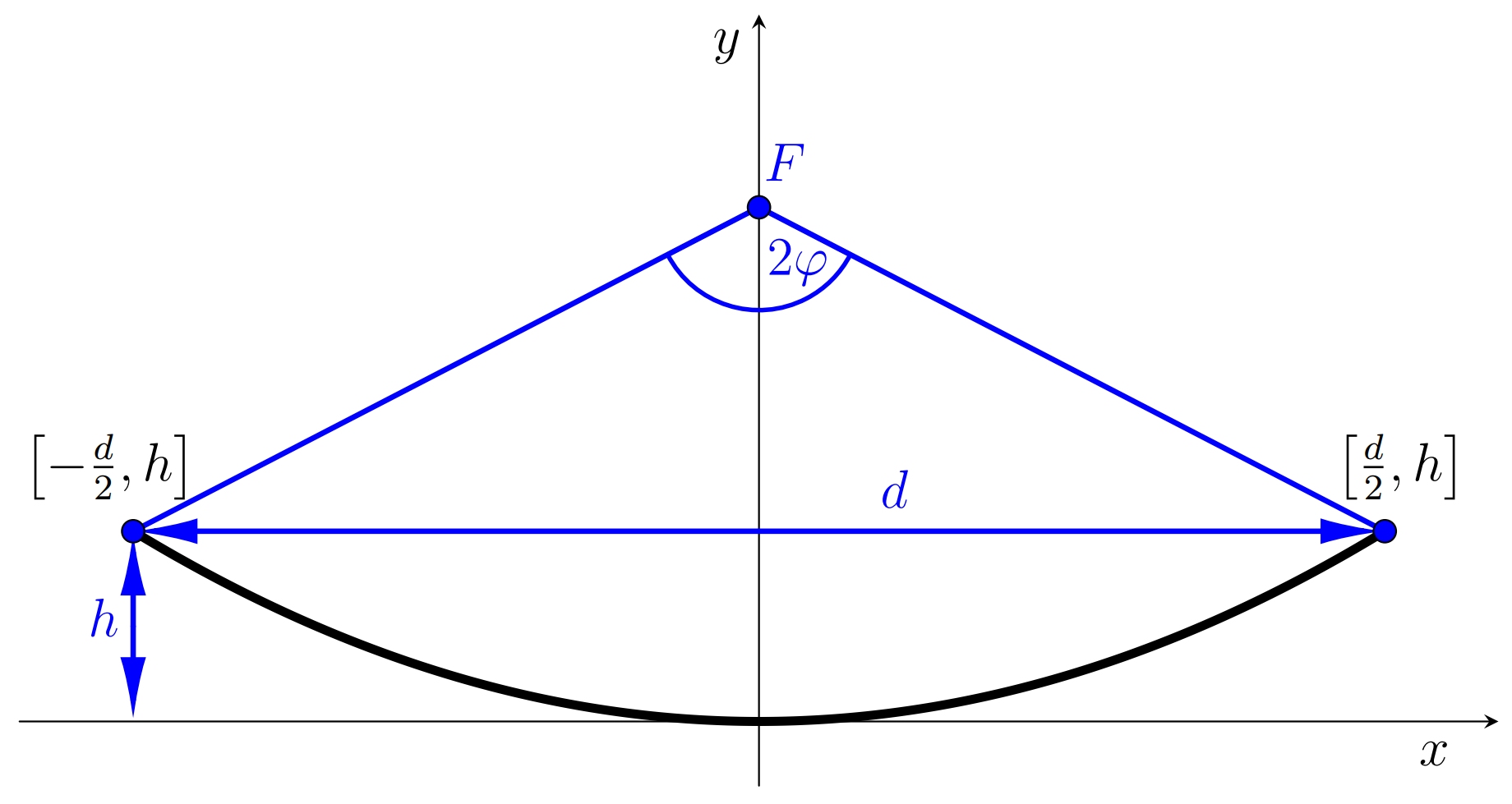
Pri výpočte polohy ohniska je výhodné predpokladať, že vrchol paraboly sa nachádza v počiatku súradnicového systému a os \(x\) je dotyčnicou paraboly v jej vrchole. Všeobecná rovnica paraboly je potom \[x^2=2py,\] kde \(p\) je parameter paraboly, t. j. vzdialenosť ohniska od riadiacej priamky paraboly. Pre parameter \(p\) platí \(p=2f\).
Zadanie
Úloha 1. Máme parabolickú anténu s priemerom \(d=120\,\text{cm}\) a hĺbkou \(h=20{,}3\,\text{cm}\). Takáto anténa je vhodná na použitie v amatérskom rádiovom pásme \(5{,}76\,\text{GHz}\) (vlnová dĺžka \(5{,}2\,\text{cm}\)). Vypočítajte optimálne umiestnenie prijímača.
Riešenie. Aby anténa fungovala optimálne, prijímač musí byť umiestnený v ohnisku parabolickej antény. Preto musíme určiť súradnice ohniska. Pri danom umiestnení paraboly majú jej krajné body súradnice \(\left[-\frac{d}{2},h\right]\) a \(\left[\frac{d}{2},h\right]\). Okrem toho oba tieto body musia spĺňať všeobecnú rovnicu paraboly \(x^2=2py,\) kde parameter \(p\) určuje polohu ohniska, pričom v našom označení platí \(f=\frac{p}{2}\).
Dosadime pravý krajný bod do tejto rovnice a určíme \(p\): \[60^2=2p\cdot 20{,}3.\] Odtiaľ \(p \doteq 88{,}7\,\text{cm}\). Ohnisko leží na osi \(y\) vo vzdialenosti \(f=\frac{p}{2}\doteq44{,}3\,\text{cm}\) od vrcholu paraboly.
Úloha 2. Určte kvadratickú funkciu (vo všeobecnom tvare) vyjadrujúcu zakrivenie parabolickej antény a znázornite ju (napr. v GeoGebre).
Riešenie. Z vrcholového tvaru rovnice paraboly \(x^2=2\cdot 88{,}7 y\) je potrebné vyjadriť súradnicu \(y\). Pre kvadratickú funkciu platí \[ y=\frac{1}{177{,}4}x^2. \] Graf kvadratickej funkcie správne zachytáva zakrivenie parabolickej antény, ak majú obe osi rovnaké mierky.
Úloha 3. Vypočítajte uhol otvorenia paraboly \(2\varphi\).
Riešenie. Pre výpočet otvorenia paraboly použijeme pravouhlý trojuholník s odvesnami dĺžok \(f-h\) a \(\frac{d}{2}\).
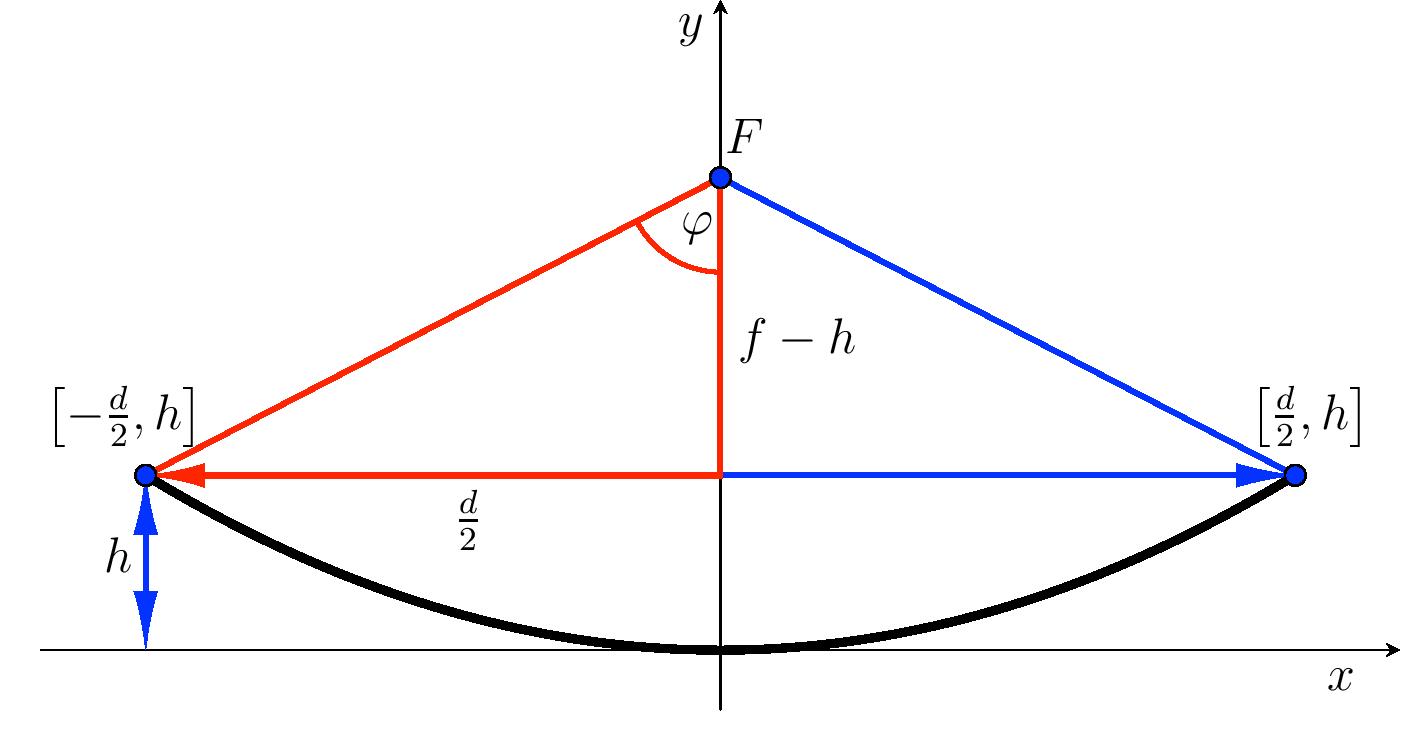
Pre polovicu uhla otvorenia platí \[ \mathrm{tg}\,\varphi=\frac{\frac{d}{2}}{f-h}=\frac{60}{44{,}3-20{,}3}\quad\Longrightarrow\quad \varphi\doteq 68{,}2^{\circ}. \] Uhol otvorenia paraboly \(2\varphi\) je \(136{,}4^{\circ}\).
Literatúra
- Střihavka, František. Parabolické antény [1994] [online]. Dostupné z https://www.ok2kkw.com/next/ok1ca_1994dish.htm [cit. 30.,10.,2023]
- Kusala, Jaroslav. Radarové antény [online]. Dostupné z https://www.army.cz/images/id_8001_9000/8753/radar/k25.htm [cit. 30.,10.,2023].
- Interactive mathematics. The Parabola [online]. Dostupné z https://www.intmath.com/plane-analytic-geometry/4-parabola.php [cit. 30.,10.,2023].