Antena paraboliczna
 20 min.,
20 min.,  2/3
2/3 Wysokiej jakości antena jest jednym z najważniejszych elementów każdego radaru. Jednym z typów anten jest tak zwana antena paraboliczna. Antena ta ma kształt obracającej się paraboloidy (co oznacza, że została stworzona poprzez obracanie części paraboli wokół jej osi) i jest używana nie tylko do radiolokacji, ale także na przykład do odbioru programów telewizji satelitarnej.
Paraboliczny kształt anteny odbiorczej zapewnia, że sygnały przychodzące z określonego kierunku są skoncentrowane w jednym punkcie po odbiciu od anteny. Mianowicie w ognisku paraboli, której obrót utworzył antenę. Odbiornik anteny znajduje się zatem w tym punkcie. Z drugiej strony, jeśli wyjście generatora wysokiej częstotliwości (emitera) znajduje się w punkcie centralnym, antena działa jak nadajnik. Po odbiciu od paraboloidy energia z emitera jest koncentrowana w wąski strumień mikrofal o równoległych wiązkach.
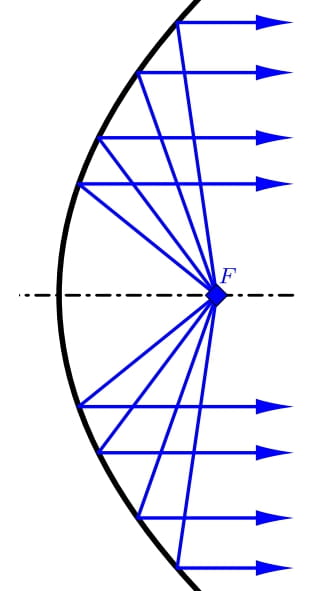
Przekrój osiowy anteny jest częścią paraboli. Charakteryzuje się on dwoma parametrami. Są to średnica \(d\) anteny i głębokość \(h\) anteny, patrz rysunek. Te dwa parametry określają położenie ogniska \(F\). Odległość ogniska od wierzchołka paraboli oznaczamy przez \(f\). Ostatnią ważną cechą anteny jest jej kąt rozwarcia, który wyraża kąt, przy którym krawędzie części paraboli są widoczne z punktu centralnego. Oznaczamy jego wartość przez \(2\varphi\).
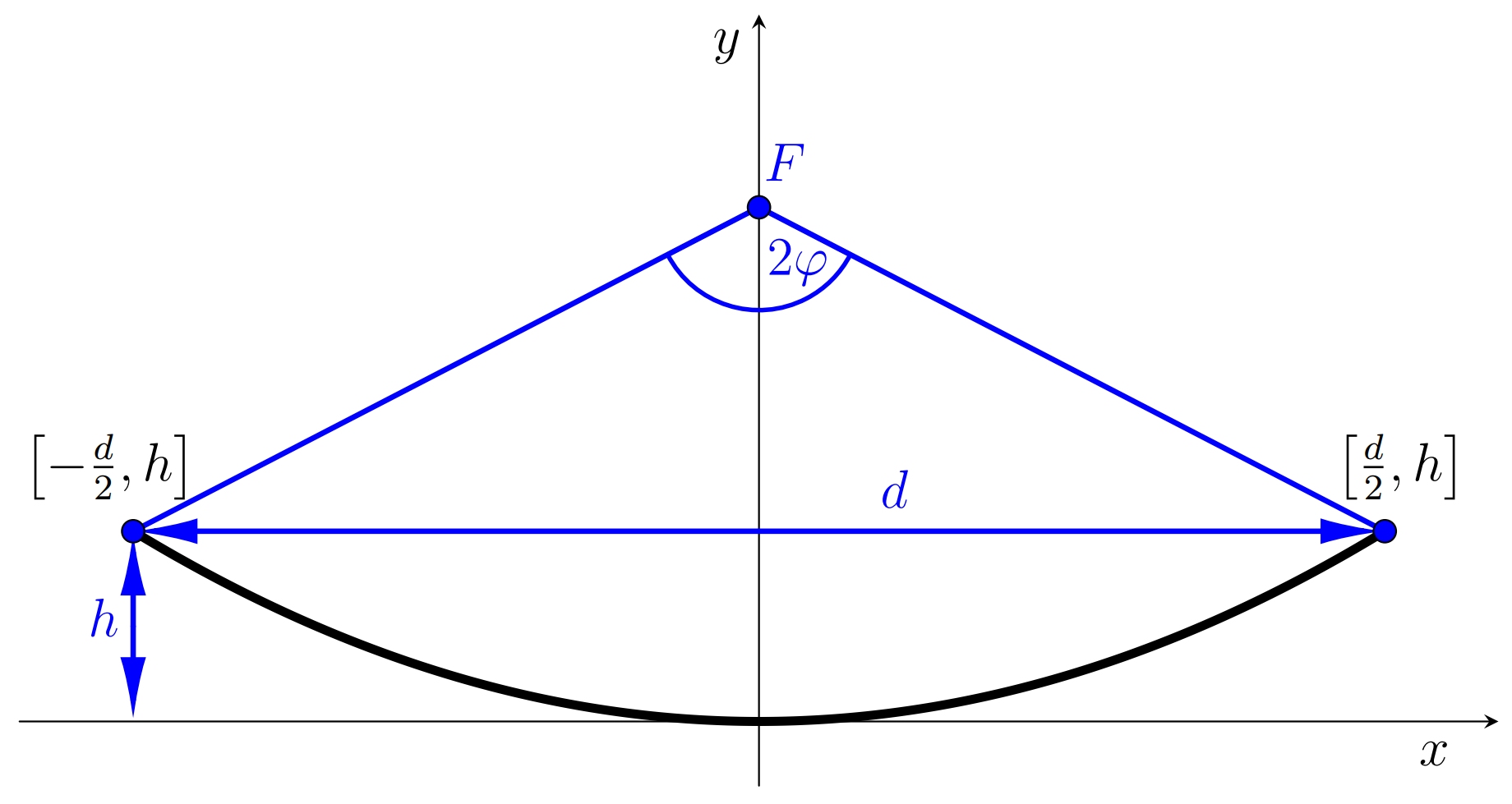
Przy obliczaniu położenia punktu ogniskowania korzystne jest założenie, że położenie wierzchołka paraboli znajduje się w punkcie początkowym układu współrzędnych, a oś \(x\) jest styczną do paraboli w jej wierzchołku. Standardowe równanie paraboli to zatem \[x^2=2py,\] gdzie \(p\) jest parametrem paraboli (semi-latus rectum), tj. odległością ogniska od direktora paraboli. Dla parametru \(p\), \(p=2f\) posiada.
Przydział
Ćwiczenie 1. Mamy antenę paraboliczną o średnicy \(d=120\,\text{cm}\) i głębokość \(h=20{,}3\,\text{cm}\). Taka antena nadaje się do użytku w amatorskim paśmie radiowym \(5{,}76\,\text{GHz}\) (długość fali \(5{,}2\,\text{cm}\)). Określenie optymalnej lokalizacji odbiornika.
Rozwiązanie. Aby antena działała optymalnie, odbiornik musi znajdować się w ognisku anteny parabolicznej. Dlatego musimy określić współrzędne punktu ogniskowego. Biorąc pod uwagę położenie paraboli, jej punkty końcowe mają współrzędne
\(\left[-\frac{d}{2},h\right]\) i \(\left[\frac{d}{2},h\right]\).
Co więcej, oba te punkty muszą spełniać standardowe równanie paraboli \(x^2=2py,\) gdzie parametr \(p\) określa pozycję fokusa, podczas gdy \(f=\frac{p}{2}\) ma zastosowanie w naszej notacji.
Podstawmy prawy punkt końcowy do tego równania i określmy \(p\): \[ 60^2=2p\cdot 20{.}3. \] Stąd \(p \doteq 88{,}7\,\text{cm}\). Ostrość leży na osi \(y\) w odległości \(f=\frac{p}{2}\doteq44{,}3\,\text{cm}\) od wierzchołka paraboli.
Ćwiczenie 2. Wyznacz funkcję kwadratową (w jawnej postaci) wyrażającą krzywiznę anteny parabolicznej i sporządz jej wykres (np. w programie GeoGebra).
Rozwiązanie. Ze standardowego równania paraboli \(x^2=2\cdot 88{,}7 y\) konieczne jest wyrażenie współrzędnej \(y\). Dla funkcji kwadratowej stosuje się
\[ y=\frac{1}{177{,}4}x^2. \]
Wykres funkcji kwadratowej poprawnie oddaje krzywiznę anteny parabolicznej, jeśli obie osie mają tę samą skalę.
Ćwiczenie 3. Oblicz kąt rozwarcia \(2\varphi\) paraboli.
Rozwiązanie. Aby obliczyć rozwarcie paraboli, użyjemy trójkąta prostokątnego o nogach długości \(f-h\) i \(\frac{d}{2}\).
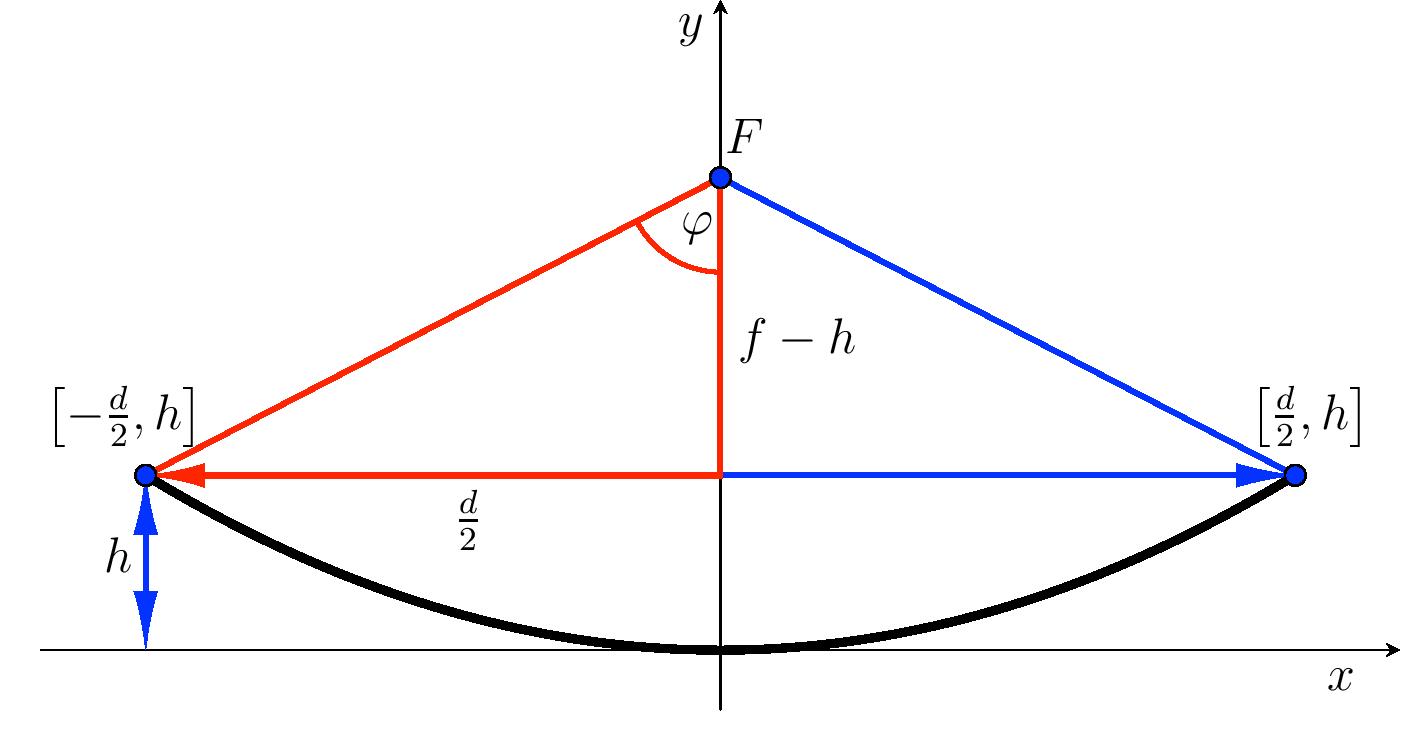
Dla połowy kąta otwarcia otrzymujemy
\[\mathrm{tg}\,\varphi=\frac{\frac{d}{2}}{f-h}=\frac{60}{44{,}3-20{,}3}\quad\Longrightarrow\quad \varphi\doteq 68{,}2^{\circ}.\]
Kąt rozwarcia paraboli \(2\varphi\) jest \(136{,}4^{\circ}\).