Zborcený hranol
 45 min.,
45 min.,  1/3
1/3 Jak vytvořit zborcený hranol z kolmého čtyřbokého hranolu
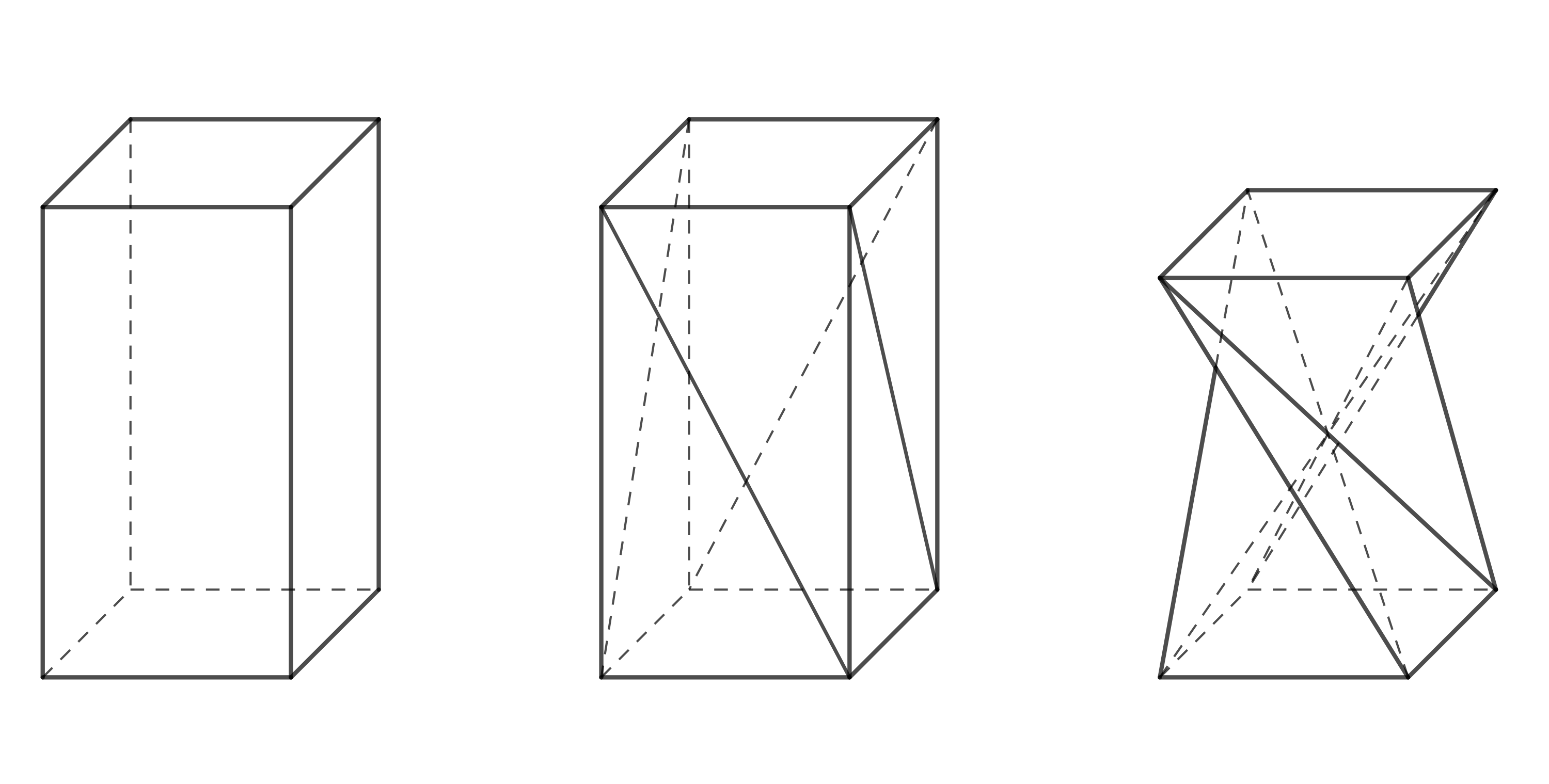
V designu nábytku se objevuje tvar, který je zajímavý i z geometrického hlediska. Lze ho vytvořit z pravidelného čtyřbokého hranolu rozdělením každé boční stěny na dva trojúhelníky pomocí jedné z úhlopříček a pootočením horní podstavy o \(90^\circ\) tak, jak je to znázorněno na Obrázku 1. Při zachování délek hran a úhlopříček současně dochází ke změně výšky hranolu. Výsledný tvar je speciálním případem tzv. zborceného hranolu (v angličtině twisted prism).
Zkusme si tento tvar vytvořit třeba z krabičky od dětského sirupu nebo očních kapek. Aby vše fungovalo je nutné, aby víčka krabičky (horní a dolní podstava hranolu) byla čtvercová a daly se nějakým způsobem odklopit nebo rozložit. K vytvoření zborceného hranolu je třeba trochu praxe a zručnosti, protože ono pootočení o \(90^\circ\) nelze provést v praxi tak jednoduše.
Můžeme použít následující postup.
- Odklopíme víčka krabičky a krabičku složíme do roviny (dvě boční stěny nahoře, dvě boční stěny dole).
- Všechny boční stěny rozdělíme úhlopříčkami v jednom směru tak, jak je to na obrázku. Snažíme se v papíru vytvořit rýhy, v nichž půjde papír přehnout.
- Všechny vzniklé úhlopříčky prolomíme mírně směrem dovnitř.
- Provedeme překřížení. Spodní část přidržíme lehce jednou rukou, vrchní část vezmeme, nadzvedneme a přesuneme směrem doleva.
- Nyní z roviny rozložíme krabičku do prostoru. Tento krok chce trochu cviku. Můžeme to udělat tak, že v místě, kde leží všechny označené úhlopříčky nad sebou, přitlačíme krabičku dvěma prsty proti sobě. Současně se snažíme druhou rukou rozložit horní nebo dolní část krabičky do prostoru.
- Pokud se vám předchozí krok podařil, zbývá už jen zavřít víčka krabičky a máte hotovo. Gratuluji!

Úloha 1. Chceme vytvořit stoličku ve tvaru zborceného hranolu a máme k dispozici několik vhodných kartonových krabic. Tyto krabice mají stejné čtvercové podstavy o délce hrany \(40\,\text{cm}\), ale různé výšky. Pro sezení máme odzkoušené, že nám vyhovuje výška stoličky \(50\,\text{cm}\). Jaká výška krabice je ideální pro výrobu stoličky ve tvaru čtyřbokého zborceného hranolu o výšce \(50\,\text{cm}\)? Délka hrany podstavy je \(a=40\,\text{cm}\).
Řešení. Původní boční hrana hranolu o délce \(v\), výška židličky \(h\) a hrana dolní podstavy \(a\) tvoří pravoúhlý trojúhelník. Hrana \(a\) je kolmým průmětem hrany \(v\) do roviny dolní podstavy (viz obrázek).
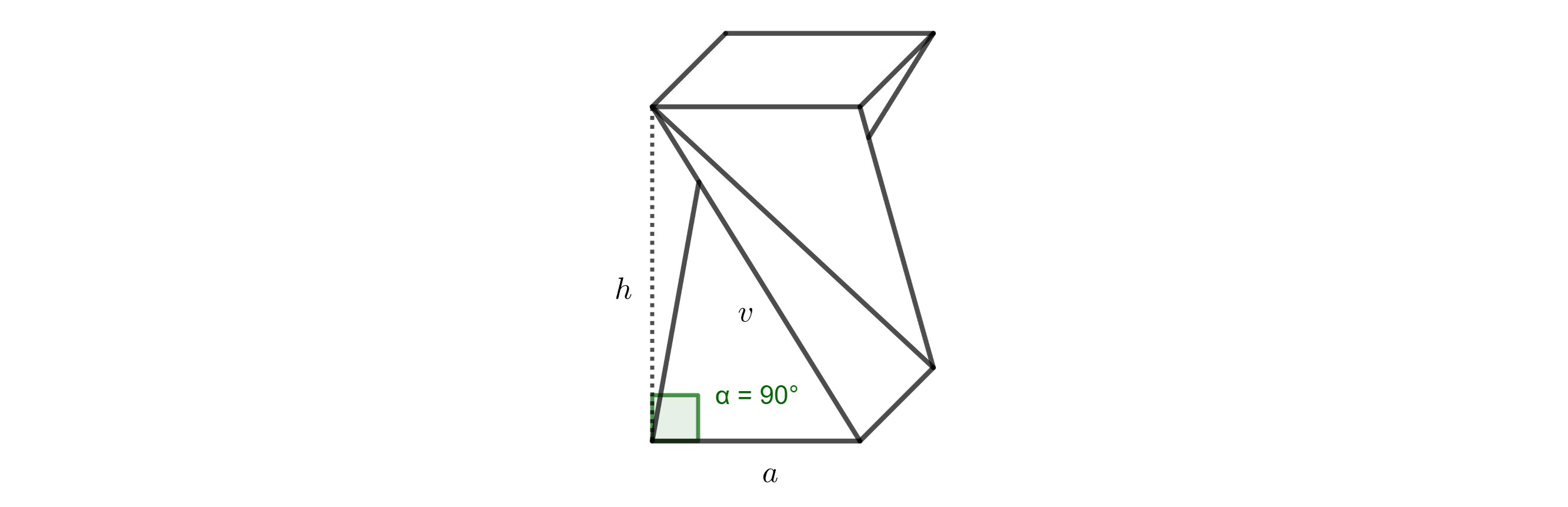
Podle Pythagorovy věty tedy platí
\[ v = \sqrt{h^2 + a^2} = \sqrt{50^2 + 40^2} \doteq 64\,\text{cm}. \]
Kartonová krabice by v ideálním případě měla být vysoká přibližně \(64\,\text{cm}\).
Další varianty zborcených hranolů
Šlo by obdobný tvar vytvořit i z kolmých hranolů, jejichž podstava by byl jiný pravidelný \(n\)-úhelník? Odpověď zní ano. Postup uvedený výše (pro tvorbu zborceného hranolu z papíru) je však možné aplikovat pouze pro sudá \(n\).
V následující úloze se budeme zabývat tvorbou šestibokého zborceného hranolu. Rozmyslete si nejdříve, o kolik stupňů se tomto případě horní podstava pootočí. Pokud prostorová představivost selhává, vytvořte si model. Pro jednoduchost stačí pracovat se sítí pláště hranolu. Na obrázku níže je taková síť již připravená ke slepení (ideální je tvrdší papír).
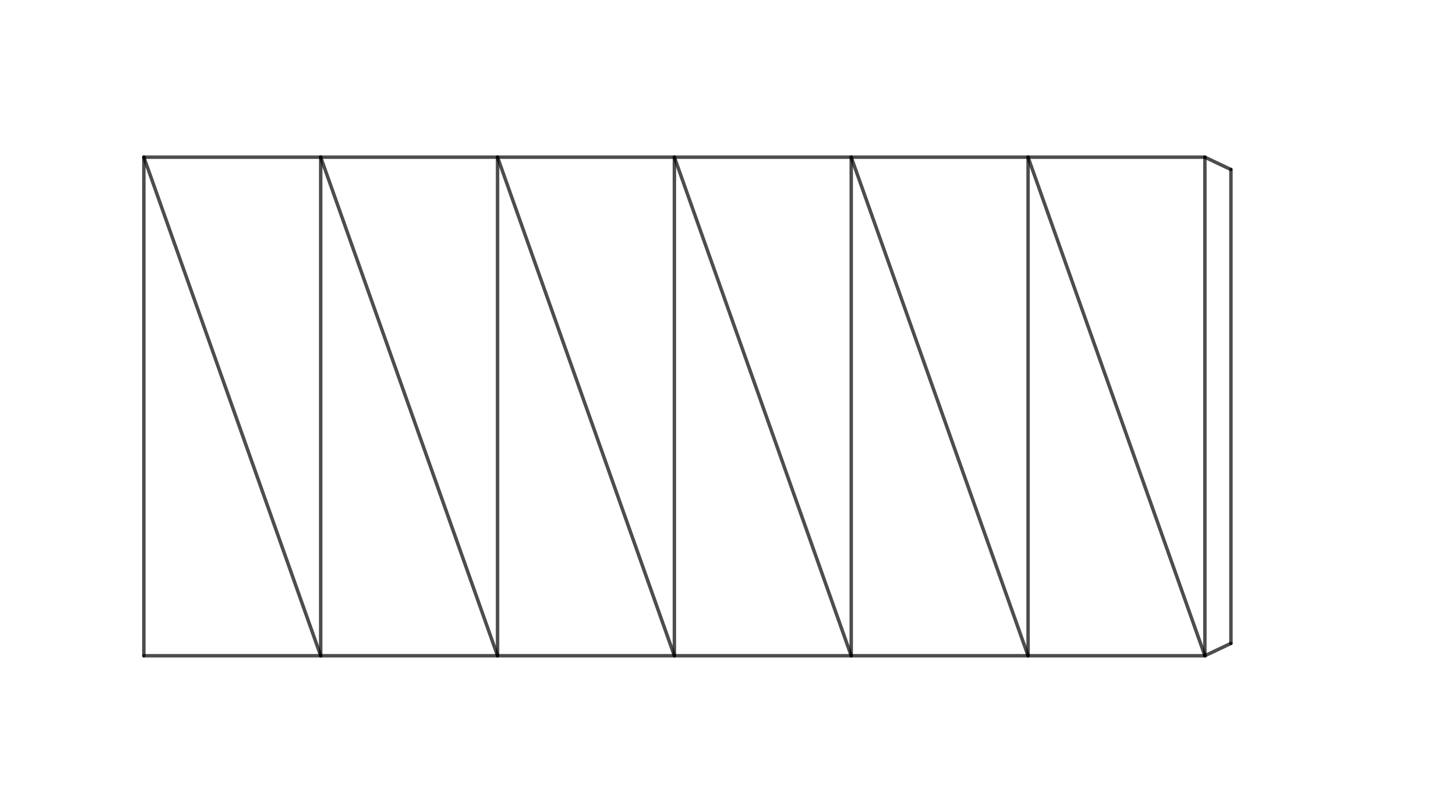
Před slepením vytvořte ohyby v hranách a úhlopříčkách. Ve hranách směrem nahoru, v úhlopříčkách směrem dolů. Po slepení postupujte podle obrázku.

Úloha 2. Jak závisí výška \(h\) šestibokého zborceného hranolu (který vznikne z pravidelného šestibokého hranolu) na výšce původního hranolu \(v\) a na délce hrany dolní podstavy \(a\)?
Řešení. K výpočtu je třeba znát úhel o který se jedna podstava pootočí vzhledem k druhé. Ten lze určit z modelu popsaného výše. Následující prostorový obrázek úhel rotace prozrazuje.
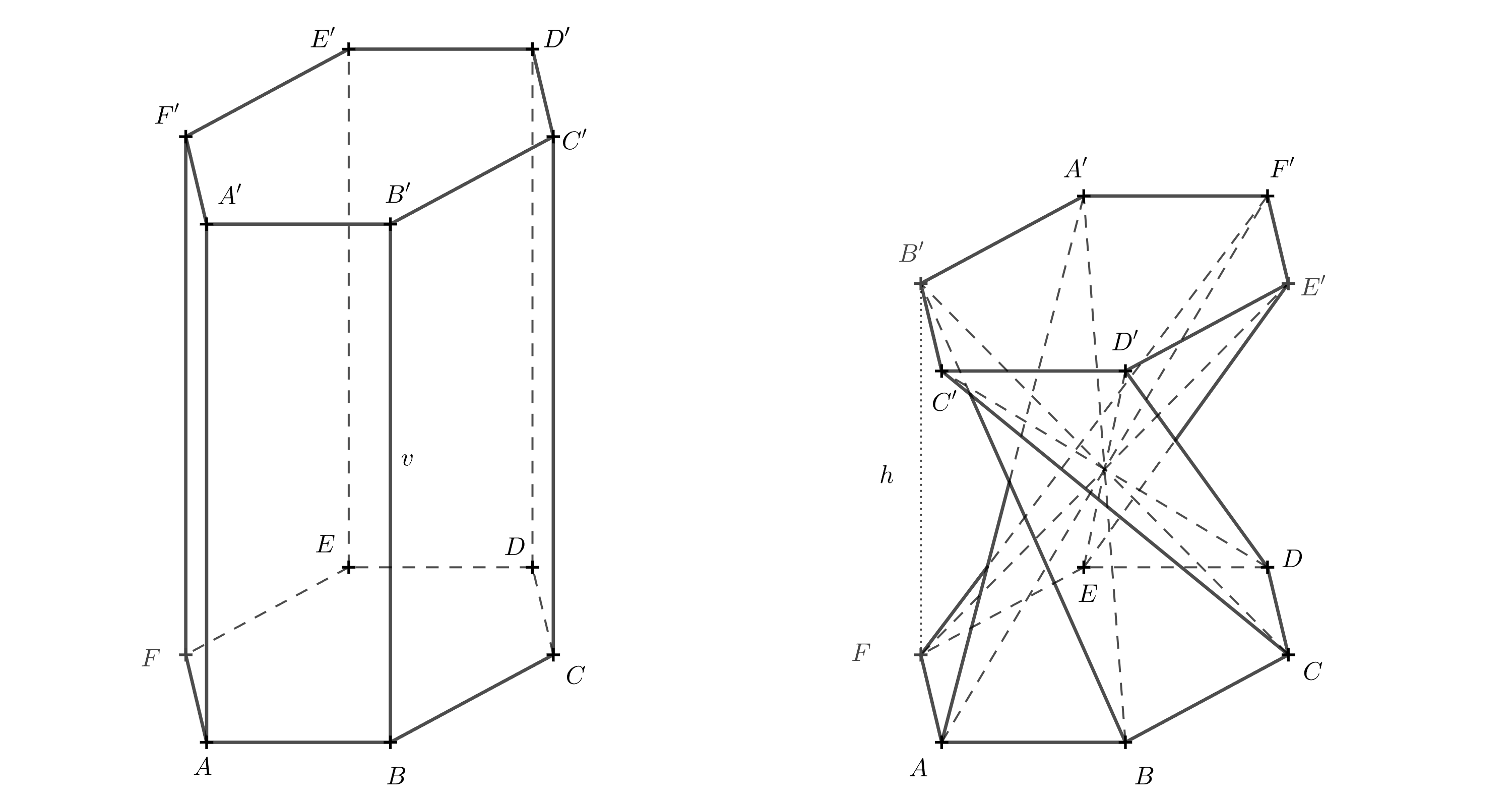
Pokud je pro někoho trojrozměrný obrázek nepřehledný, může si představit, jak těleso vypadá při pohledu shora. Horní podstavu budeme brát nyní jako průhlednou. Úsečky, které byly úhlopříčkami ve stěnách původního hranolu, se protínají v jednom bodě a při pohledu shora dělí šestiúhelník \(A'B'C'D'E'F'\) na šest rovnostranných trojúhelníků. Zaměříme se na úsečku \(A'B\), která byla úhlopříčkou ve stěně \(ABB'A'\).
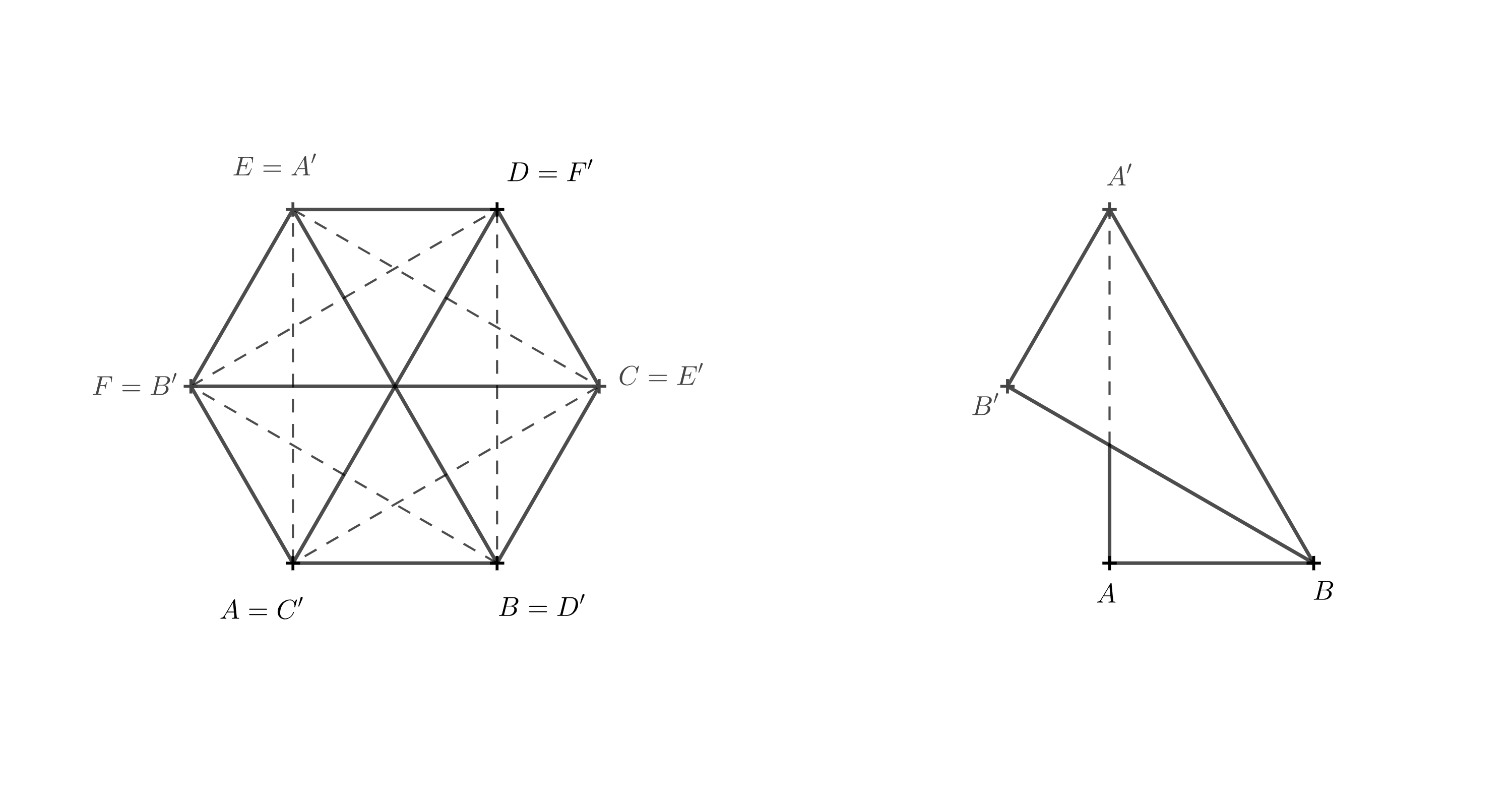
Aby tato úsečka procházela středem, musí být \(A'=E\), protože bod \(E\) je naproti bodu \(B\). Ostatní vrcholy doplníme postupně podle abecedy ve stejném směru, v jakém jsou body označeny v dolní podstavě, tj. proti směru hodinových ručiček.
Nyní je už jasné, že se horní podstava pootočila vzhledem ke spodní podstavě o \(120^\circ\). Díky tomu víme, že hrana \(BB'\) leží nad hranou \(BF\) a úsečka \(BF\) je kolmým průmětem úsečky \(BB'\).
Délka hrany \(BB'\) je \(v\), délku \(BF\) označme \(v_1\). Výška tělesa \(h\) je rovna délce úsečky \(B'F\). Body \(F\), \(B\) a \(B'\) tvoří pravoúhlý trojúhelník. Pomocí Pythagorovy věty dostáváme pro výšku vztah
\[ h = \sqrt{v^2 - v_1^2}. \]
Zbývá určit \(v_1\). K tomu použijeme trojúhelník \(ABF\).
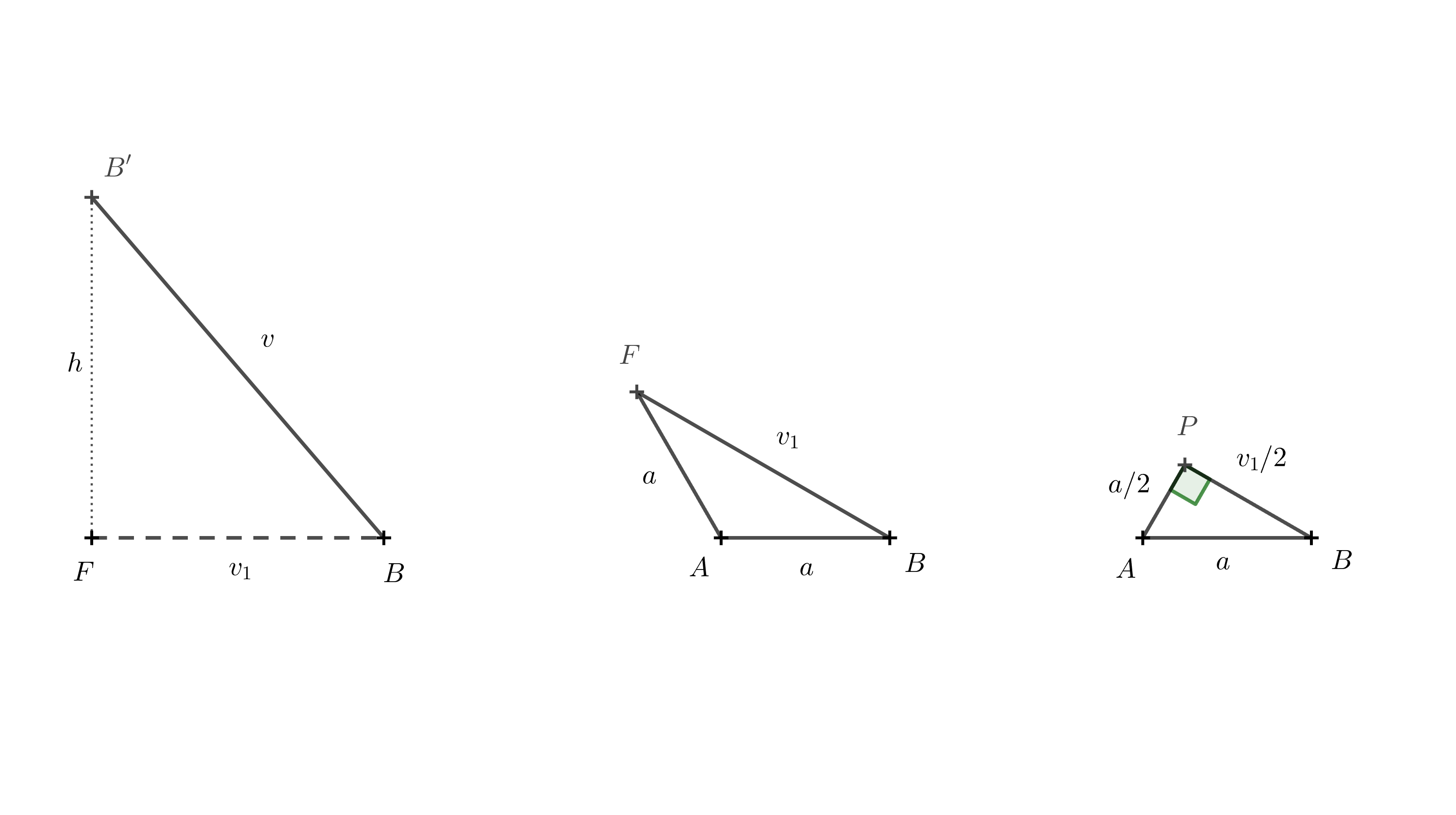
Postupovat můžeme opět pomocí Pythagorovy věty. K vytvoření pravoúhlého trojúhelníka stačí bodem \(A\) vést výšku na stranu \(AF\). Patu této výšky označíme \(P\). Délka této výšky je \(\frac a2\), protože trojúhelník \(ABP\) je polovina rovnostranného trojúhelníku o straně \(a\). Platí
\[ \frac{v_1}{2} = \sqrt{a^2 - \left(\frac{a}{2}\right)^2} = \sqrt{\frac{3}{4}a^2} = \frac{a}{2}\sqrt{3} \]
a odtud
\[ v_1 = a\sqrt{3}. \]
Toto vyjádření nyní můžeme dosadit do vztahu pro \(h\). Tím dostáváme
\[ h = \sqrt{v^2 - (a\sqrt{3})^2} = \sqrt{v^2 - 3a^2}, \]
což je hledané vyjádření výšky šestibokého zborceného hranolu pomocí \(v\) a \(a\).
Úloha 3. Jaká je omezující podmínka pro vznik modelů z předchozích dvou úloh?
Řešení. V Úloze 1 musí být \(v\) větší než \(a\). Pokud by platila rovnost \(v=a\), potom by v pravoúhlém trojúhelníku byla přepona stejně dlouhá jako odvěsna a zbylá odvěsna by měla nulovou délku. Výška zborceného hranolu by tedy byla nulová a hranol by se složil do roviny. Úhlopříčky původního hranolu by se stále protínaly v jednom bodě.
V Úloze 2 by obdobně muselo platit \(v > |AE|\), tedy \(v > \sqrt{3}a\). Pro \(v=\sqrt{3}a\) by zborcený hranol měl opět nulovou výšku a složil by se do roviny.
Postup pro liché \(n\)
Už bylo zmíněno, že pro liché \(n\) nelze postupovat tak, jak bylo uvedeno výše. Rozdíl je ale pouze v tom, že po vytvoření sítě pláště není vhodné lepit spoj v boční hraně předtím než vytvoříme požadovaný tvar. Nejdříve síť upravíme do tvaru zborceného hranolu a teprve poté slepíme boční hranu.
Postup pro jiný úhel otočení
Co kdybychom chtěli vyrobit tvar podobný tomu z prvního příkladu, ale použít ho jako vázičku na suché květiny nebo stojan na tužky? Nevyhovuje nám v tom případě, že se 4 hrany zborceného hranolu (bývalé úhlopříčky stěn pravidelného čtyřbokého hranolu) uprostřed hranolu protínají. Chceme, aby uvnitř vznikl volný prostor. Proto potřebujeme zmenšit úhel rotace jedné podstavy vzhledem k druhé.
Úloha 4. Sestrojte síť vázy tvaru zborceného hranolu, jestliže je dána výška vázy \(h=110\,\text{mm}\), délka hrany čtvercové podstavy \(a=65\,\text{mm}\) a úhel rotace horní hrany vázy oproti dolní podstavě je \(\alpha=45^\circ\). Tentokrát úlohu řešte konstrukčně, tedy pomocí pravítka a kružítka.
Nápověda. Na obrázku vlevo je pohled shora na dolní podstavu a na horní podstavu pootočenou o \(45^\circ\). Napravo jsou znázorněny i všechny hrany vzniklého objektu. Kreslit všechny hrany není třeba, pro konstrukci je důležitá spojnice \(AA'\) a \(BA'\). Je třeba si také uvědomit, že při pohledu shora pro kolmý průmět \(A_1\) bodu \(A'\) do roviny dolní podstavy platí \(A_1=A'\).
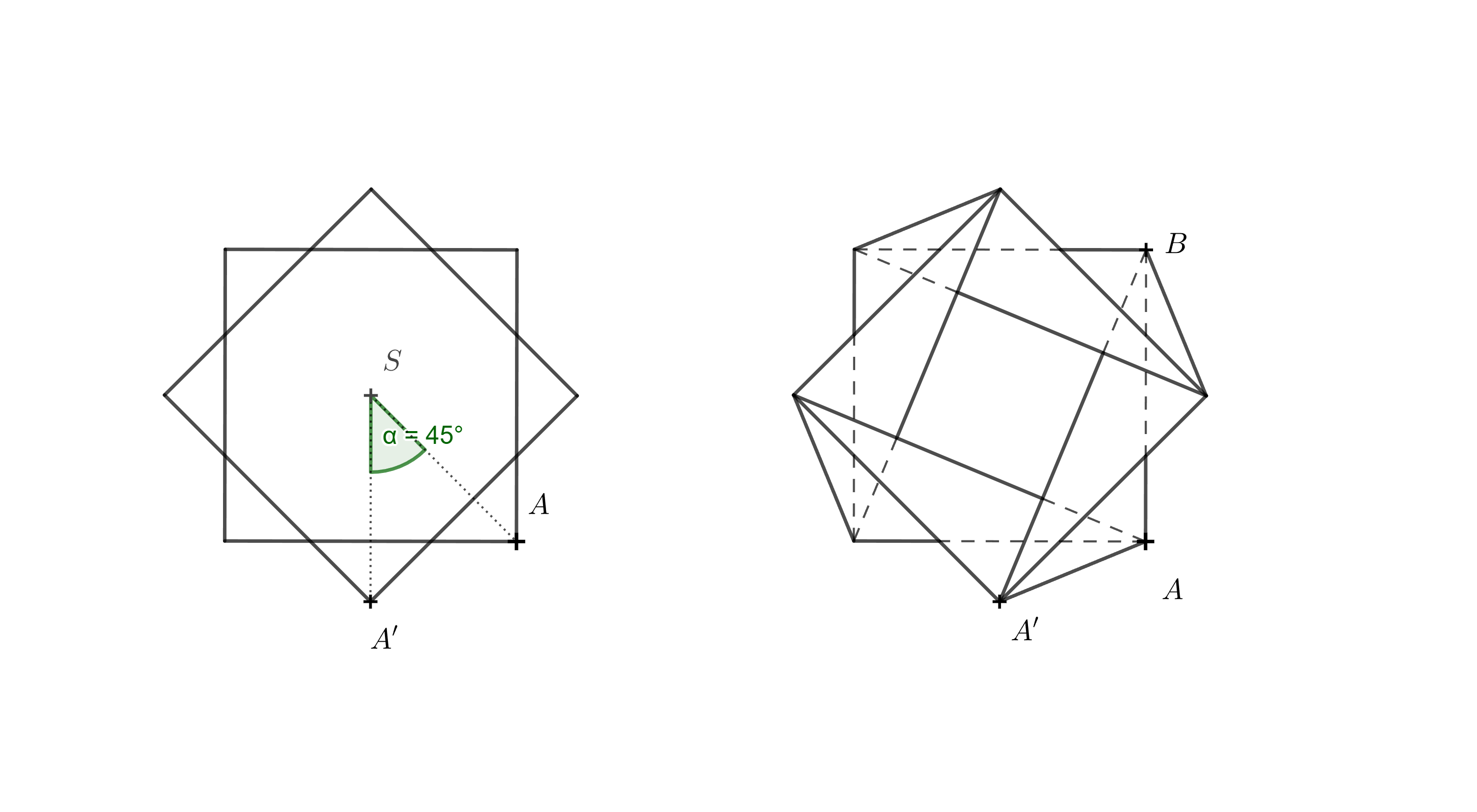
Ze zadání navíc víme, že výška vázy je \(110\,\text{mm}\), tedy \(|AA_1|=110\,\text{mm}\). Z pravoúhlého trojúhelníka \(A_1AA'\) můžeme určit skutečnou délku hrany \(AA'\). Obdobně můžeme určit délku hrany \(BA'\) pomocí konstrukce pravoúhlého trojúhelníka \(A_1BA'\). Poté známe všechny délky hran potřebné pro narýsování sítě vázy.
