Řešením ryze matematických problémů dostáváme přesné výsledky. Používáme-li však matematiku k řešení problémů světa kolem nás, dosáhneme absolutní přesnosti odpovědi jen zřídka. Přibližnost je někdy způsobena tím, že při svých úvahách reálnou situaci zjednodušíme. Jindy jsou přibližně stanovena už vstupní data (např. měřit délky nebo čas umíme jen s omezenou přesností) nebo je absolutně přesný výsledek reálně nedosažitelný a musí se zaokrouhlit.
Často se v praxi (a také v následujících úlohách) využívá zaokrouhlování na určitý počet platných číslic. Kladné reálné číslo \(r\) zaokrouhlíme na \(n\) platných číslic následujícím způsobem:
Úloha 1. Vedoucí skladu léčiv obdržel fakturu za objednané dva druhy vakcín. Celkem bylo za dodávku \(597\) balení vakcín Ixodinum proti encefalitidě a \(386\) balení vakcín Nopolio proti obrně zaplaceno \(401\,950\,\text{Kč}\). Při vstupní kontrole však bylo zjištěno, že \(84\) balení vakcíny Ixodinum a \(19\) balení vakcíny Nopolio je prošlých a musí být vráceny. Při reklamaci prošlých léčiv bylo vráceno \(39\,600\,\text{Kč}\).
Protože je zvědavý, chce si spočítat, jaká je nákupní cena jednoho balení obou vakcín. Nemá však po ruce kalkulačku a ani telefon, a proto se spokojí s přibližným řešením. Všechny údaje, které zná, před výpočtem zaokrouhlí na jednu platnou číslici.
Jak moc se bude jeho výsledek lišit od skutečné nákupní ceny? Pro oba druhy vakcín určete absolutní rozdíl vypočítané a skutečné ceny i relativní chybu v procentech.
Řešení. Vyřešme úlohu nejprve bez zaokrouhlování. Označme \(x\) cenu za jedno balení Ixodinu a \(y\) cenu za jedno balení Nopolio. Informace v zadání vedou na soustavu dvou lineárních rovnic o dvou neznámých \[ \begin{alignedat}{2} 597x &\,+& 386 y &= 401\,950 \\ 86x &\,+& 19 y &= 39\,600, \end{alignedat} \] jejímž řešením dostáváme skutečnou nákupní cenu jednoho balení vakcíny Ixodinum \(350\,\text{Kč}\) a cenu jednoho balení vakcíny Nopolio \(500\,\text{Kč}\).
Po zaokrouhlení koeficientů na jednu platnou číslici řešíme soustavu \[ \begin{alignedat}{2} 600x' &\,+ & 400 y' &= 400\,000 \\ 90x' &\,+ & 20 y' &= 40\,000. \end{alignedat} \] Řešením je dvojice \(x'=\frac{1000}{3}\doteq333\) a \(y'=500\). Porovnáme skutečnou cenu a skladníkův cenový odhad. Dále vypočteme relativní chybu v ceně léčiva, která vznikla zaokrouhlením. Relativní chybu určíme jako podíl absolutní chyby (absolutní hodnoty rozdílu cen) a skutečné ceny balení léku. Výsledky shrneme v tabulce:
| vakcína | skutečná cena | skladníkův odhad ceny | relativní chyba |
|---|---|---|---|
| Ixodinum | \(350\,\text{Kč}\) | \(333\,\text{Kč}\) | \(\frac{350-333}{350}=4{,}9\,\%\) |
| Nopolio | \(500\,\text{Kč}\) | \(500\,\text{Kč}\) | \(\frac{500-500}{500}=0\,\%\) |
Úloha 2. Po pár měsících přišla do skladu jiná dodávka, a to \(504\) balení vakcín Antiflu proti chřipce a \(81\) balení vakcín Kontradift proti záškrtu. Za tuto dodávku bylo zaplaceno \(198\,900\,\text{Kč}\). Při vstupní kontrole bylo zjištěno, že \(98\) balení Antiflu a \(18\) balení Kontradiftu je prošlých. Při jejich reklamaci bylo zpět vráceno \(40\,700\,\text{Kč}\).
Vedoucí skladu zopakoval svůj postup a spočítal si od ruky přibližnou nákupní cenu obou léků. Tentokrát se však nestačil divit. Z čeho vycházel jeho údiv a jak moc se jeho výsledek od skutečných cen lišil tentokrát?
Řešení. Úlohu budeme řešit stejně jako předchozí, tentokrát označíme \(x\) cenu jednoho balení Antiflu a \(y\) cenu jednoho balení Kontradiftu. Tyto skutečné ceny jsou řešením soustavy \[ \begin{alignedat}{2} 504x &\,+ & 81 y &= 198\,900 \\ 98x &\,+ & 18 y &= 40\,700, \end{alignedat} \] odkud dostáváme \(x=250\) a \(y=900\).
Po zaokrouhlení koeficientů řešíme soustavu \[ \begin{alignedat}{2} 500x' &\,+ & 80 y' &= 200\,000 \\ 100x' &\,+ & 20 y' &= 40\,000, \end{alignedat} \] jejímž řešením je \(x'=400\) a \(y'=0\). Z řešení vedoucího skladu se tedy zdá, že druhá vakcína byla do skladu dodána zadarmo, přitom je ve skutečnosti skoro čtyřikrát dražší než první. Rozdíl mezi skutečnou cenou a skladníkovým odhadem ceny i relativní chybu zaneseme opět do tabulky:
| vakcína | skutečná cena | skladníkův odhad ceny | relativní chyba |
|---|---|---|---|
| Antiflu | \(250\,\text{Kč}\) | \(400\,\text{Kč}\) | \(\frac{400-250}{250}=60\,\%\) |
| Kontradift | \(900\,\text{Kč}\) | \(0\,\text{Kč}\) | \(\frac{900-0}{900}=100\,\%\) |
Úloha 3. Soustavy z obou předchozích úloh znázorněte graficky ve vhodném softwaru. Porovnáním znázornění soustav z Úlohy 1 se znázorněním soustav z Úlohy 2 vysvětlete rozdíl v přesnostech výsledků obou úloh.
Řešení. Označme \(p_1\), \(p_2\) (resp. \(q_1\), \(q_2\)) jednotlivé přímky dané rovnicemi soustavy s nezaokrouhlenými koeficienty v Úloze 1 (resp. v Úloze 2), jmenovitě \[ \begin{aligned} p_1 &\colon 597x + 386 y = 401\,950 \\ p_2 &\colon 86x + 19 y = 39\,600 \\[2mm] q_1 &\colon 504x + 81 y = 198\,900 \\ q_2 &\colon 98x + 18 y = 40\,700. \end{aligned} \] Přímky dané odpovídajícími rovnicemi se zaokrouhlenými koeficienty označme \(p'_1\), \(p'_2\), \(q'_1\) a \(q'_2\) a dále označme body \(P\in p_1\cap p_2\), \(P'\in p'_1\cap p'_2\), \(Q\in q_1\cap q_2\) a \(Q'\in q'_1\cap q'_2\). Grafické znázornění dvojice soustav pro každou úlohu zvlášť je vidět na obrázku.
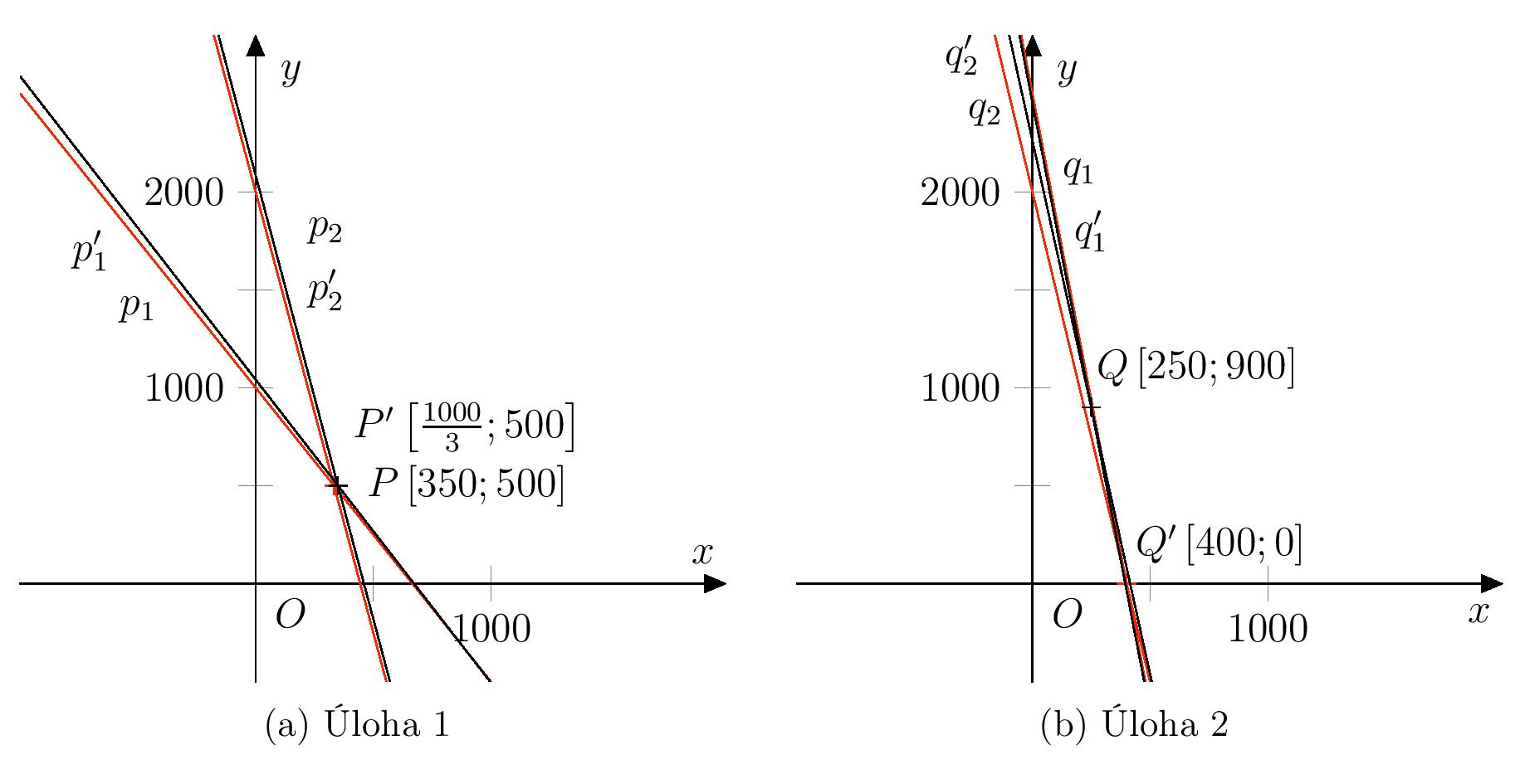
Porovnáním obou grafických znázornění je vidět, že v případě Úlohy 2 je přímky \(q_1\) a \(q_2\) jsou téměř rovnoběžné. Při zaokrouhlování koeficientů rovnice se obecně poloha přímek vůči souřadnému systému mění a tím se mění také poloha jejich průsečíku. Změna polohy průsečíku je přitom daleko větší u přímek, které jsou téměř rovnoběžné. Z obrázku je také vidět, proč bude zaokrouhlením v druhé úloze daleko více ovlivněna druhá souřadnice průsečíku (tj. cena vakcíny Kontradift). Vzhledem ke sklonu přímek \(q_1\) a \(q_2\) by totiž malá změna \(x\)-ové souřadnice průsečíku znamenala velkou změnu jeho \(y\)-ové souřadnice.