První Keplerův zákon říká:
Planety se pohybují kolem Slunce po eliptických trajektoriích, přičemž Slunce je v jednom z jejich ohnisek.
Místo na trajektorii, kde je Země nejblíže (resp. nejdále) Slunci se pak nazývá perihel (resp. afel). Situace je znázorněna na obrázku, který je záměrně zkreslený, aby byl patrný eliptický tvar trajektorie. Vzdálenosti jsou uvedeny v milionech kilometrů (data jsou z programu Stellarium a odpovídají roku 2022).
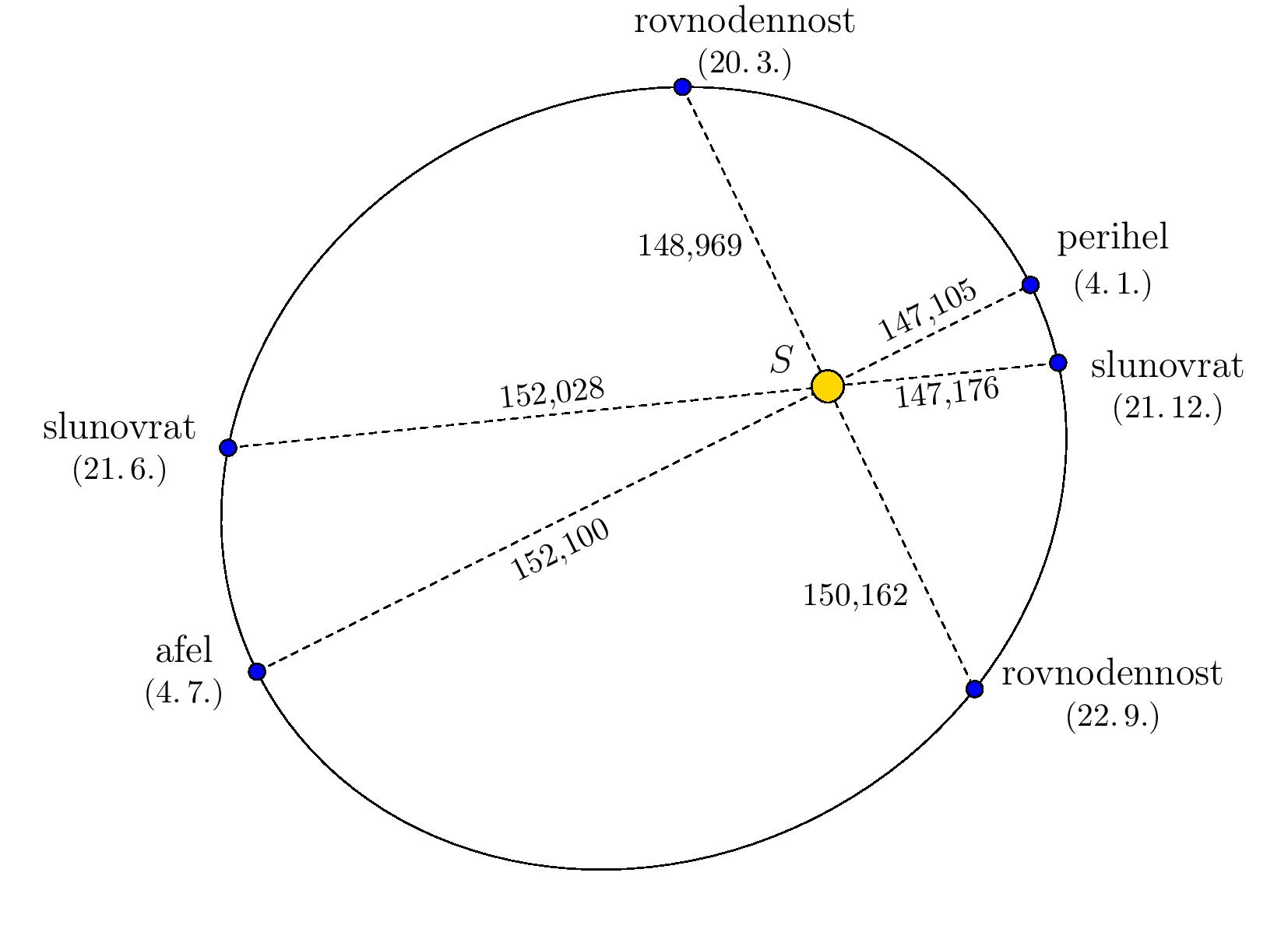
Úloha 1. Určete excentricitu a délky hlavní a vedlejší poloosy eliptické trajektorie Země užitím informací na obrázku.
Řešení. Protože se Slunce nachází v jednom z ohnisek elipsy, jsou afel a perihel její hlavní vrcholy. Součet vzdáleností Slunce od Země v afelu a perihelu je proto dvojnásobkem délky hlavní poloosy \(a\) a tedy
\[a=\frac{152{,}100\cdot10^6\,\text{km} + 147{,}105\cdot10^6\,\text{km}}{2}\doteq149,603\cdot10^6\,\text{km}.\]
Jak je patrné z obrázku (bod \(O\) zde značí střed elipsy), součet délky hlavní poloosy~\(a\) a excentricity \(e\) je vzdáleností Slunce od Země v afelu. Tedy
\[e=152,100\cdot10^6\,\text{km} - 149,603\cdot10^6\,\text{km} =2,497\cdot10^6\,\text{km}.\]
Protože pro elipsu platí vztah \(a^2 = b^2 + e^2\) (kde \(b\) je délka vedlejší poloosy), určíme nyní délku vedlejší poloosy:
\[b=\sqrt{a^2 - e^2}\doteq 149,582\cdot10^6\,\text{km}.\]
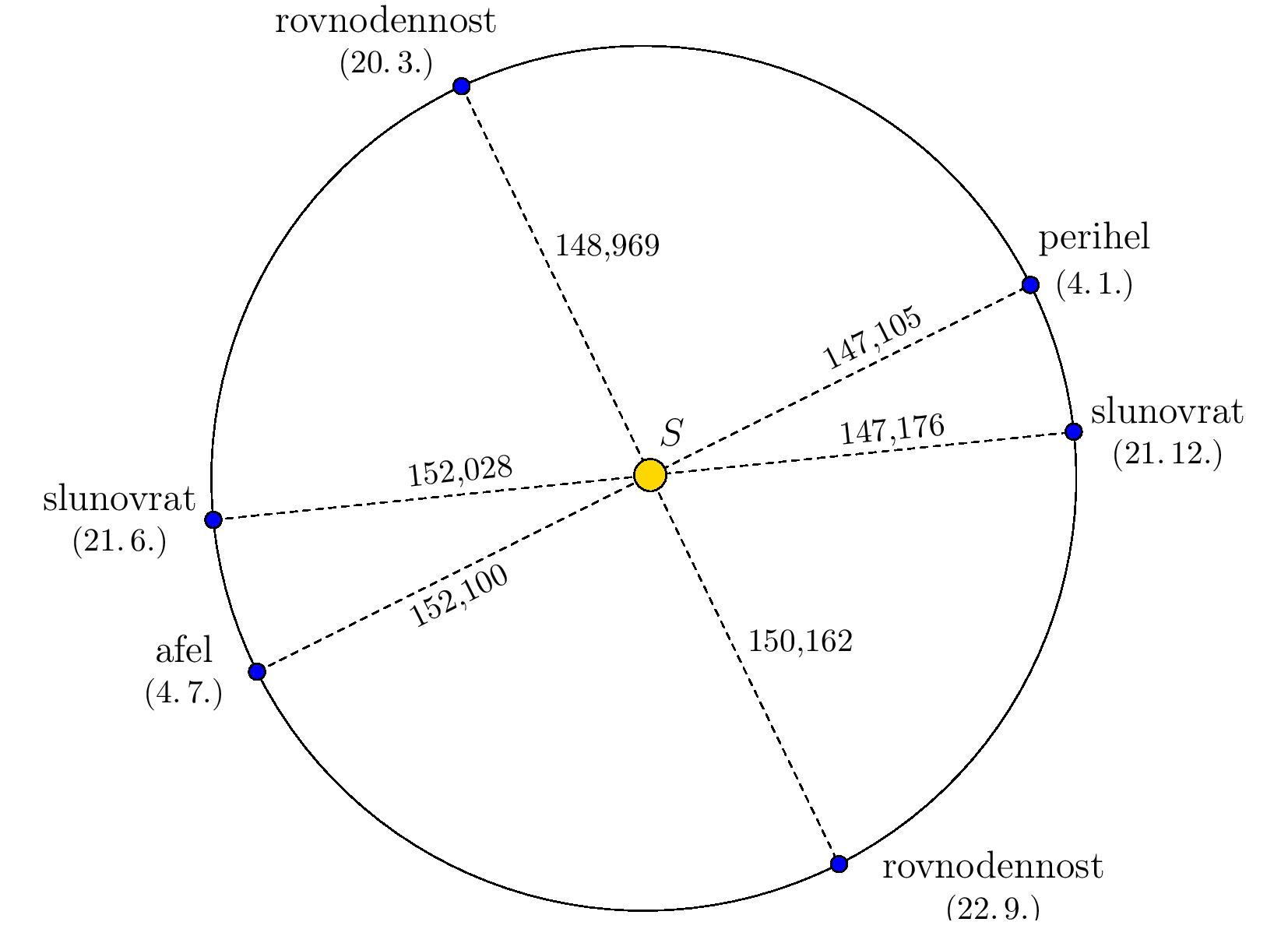
Pokud nyní obrázek ze zadání překreslíme tak, aby poměr velikostí poloos odpovídal skutečnosti, je z něj vidět, že se trajektorie skutečně velice podobá kružnici se Sluncem v jejím středu.
