Zvedavý skladník
 35 min.,
35 min.,  2/3
2/3 Pri riešení čisto matematických úloh dostávame presné výsledky. Avšak pri použití matematiky na riešenie problémov z reálneho sveta len zriedka dosiahneme absolútnu presnosť odpovede. Aproximácia je niekedy dôsledkom zjednodušenia reálnej situácie v našej mysli. Niekedy sú aj vstupné údaje aproximované (napr. dĺžky alebo čas vieme merať len s obmedzenou presnosťou), alebo je absolútne presný výsledok reálne nedosiahnuteľný a musíme ho zaokrúhliť.
V praxi (a v nasledujúcich úlohách) sa často používa zaokrúhľovanie na daný počet platných číslic. Kladné reálne číslo \(r\) zaokrúhľujeme na \(n\) platných číslic takto:
- Vyjadríme \(r\) v tvare \(a\cdot 10^b\), kde \(a\in\mathbb{R}\), \(a\in\left\langle 1,10 \right)\) a \(b\in\mathbb{Z}\), a následne zaokrúhlime číslo \(a\) na \(n-1\) desatinných miest podľa podľa bežných pravidiel zaokrúhľovania.
- Napr. čísla \(r=31{,}258\,16\) a \(s=0{,}023 \,123\,6\) zaokrúhlime na štyri platné číslice nasledovne: \[ \begin{aligned} r &= 31{,}258\,16 = 3{,}125\,816 \cdot 10^1 \quad \doteq\quad 3{,}126 \cdot 10^1 = 31{,}26 \\ s &= 0{,}023 \,123\,6 = 2{,}312\,36 \cdot 10^{-2} \quad \doteq\quad 2{,}312 \cdot 10^{-2} = 0{,}023\,12. \end{aligned} \] Zaokrúhľovanie vstupných údajov môže mať prekvapivé dôsledky na presnosť výsledku, napríklad pri riešení rovníc, ako uvidíme v nasledujúcej sérii úloh.
Úloha 1. Skladník vo farmaceutickom sklade dostal faktúru za dva druhy objednaných vakcín. Za dodávku \(597\) balení vakcíny Ixodinum proti encefalitíde a \(386\) balení vakcíny Nopolio proti detskej obrne bolo zaplatených spolu \(401\,950\,\text{Kč}\). Pri úvodnej kontrole však bolo zistené, že \(86\) balení Ixodinum a \(19\) balení Nopolio bolo expirovaných a museli byť vrátené. Za expirované lieky bolo vrátených spolu \(39\,600\,\text{Kč}\).
Zo zvedavosti si skladník chce vypočítať nákupnú cenu jedného balenia oboch vakcín. Nemá však po ruke kalkulačku ani mobil, a preto sa uspokojí s približným riešením. Všetky údaje, ktoré pozná, pred výpočtom zaokrúhli na jednu platnú číslicu.
O koľko sa jeho výsledok bude líšiť od skutočnej nákupnej ceny? Pre oba druhy vakcín určte absolútny rozdiel medzi vypočítanou a skutočnou cenou, ako aj relatívnu chybu vyjadrenú v percentách.
Riešenie. Najskôr vyriešme úlohu bez zaokrúhľovania. Nech \(x\) je cena za balenie Ixodinum a \(y\) cena za balenie Nopolio. Zadanie smeruje k zostaveniu sústavy dvoch lineárnych rovníc s dvoma neznámymi \[ \begin{alignedat}{2} 597x &\,+& 386 y &= 401\,950 \\ 86x &\,+& 19 y &= 39\,600, \end{alignedat} \] ktorej riešením je skutočná nákupná cena balenia Ixodinum \(350\,\text{Kč}\) a balenia Nopolio \(500\,\text{Kč}\).
Po zaokrúhlení koeficientov na jednu platnú číslicu riešime sústavu \[ \begin{alignedat}{2}600x' &\,+ & 400 y' &= 400\,000 \\ 90x' &\,+ & 20 y' &= 40\,000. \end{alignedat} \] Riešením je dvojica \(x'=\frac{1000}{3}\doteq333\) a \(y'=500\). Máme teda skutočnú cenu lieku a odhad ceny podľa skladníka. Vypočítajme aj relatívnu chybu ceny spôsobenú zaokrúhľovaním. Relatívna chyba je absolútna chyba (absolútna hodnota rozdielu cien) delená skutočnou cenou za balenie. Výsledky zhrnieme v tabuľke:
| vakcína | skutočná cena | skladníkov odhad ceny | relatívna chyba |
|---|---|---|---|
| Ixodinum | \(350\,\text{Kč}\) | \(333\,\text{Kč}\) | \(\frac{350-333}{350}=4{,}9\,\%\) |
| Nopolio | \(500\,\text{Kč}\) | \(500\,\text{Kč}\) | \(\frac{500-500}{500}=0\,\%\) |
Úloha 2. Po niekoľkých mesiacoch dorazila do skladu ďalšia dodávka, a to \(504\) balení vakcíny Antiflu proti chrípke a \(81\) balení vakcíny Kontradift proti záškrtu. Za túto dodávku bolo zaplatených \(198\,900\,\text{Kč}\). Pri úvodnej kontrole bolo zistené, že \(98\) balení Antiflu a \(18\) balení Kontradift bolo expirovaných. Za expirované balenia bolo vrátených spolu \(40\,700\,\text{Kč}\).
Skladník postup zopakoval a približnú cenu oboch liekov vypočítal z hlavy. Tentokrát ho však výsledok prekvapil. Čím bol prekvapený a o koľko sa jeho výsledok líšil od skutočných cien?
Riešenie. Úlohu riešime rovnako ako predtým, tentoraz označme \(x\) cenu jedného balenia Antiflu a \(y\) cenu jedného balenia Kontradift. Skutočné ceny sú riešením sústavy \[ \begin{alignedat}{2} 504x &\,+ & 81 y &= 198\,900 \\ 98x &\,+ & 18 y &= 40\,700, \end{alignedat} \] kde dostaneme \(x=250\) a \(y=900\).
Pri zaokrúhlení koeficientov riešime sústavu \[ \begin{alignedat}{2} 500x' &\,+ & 80 y' &= 200\,000 \\ 100x' &\,+ & 20 y' &= 40\,000, \end{alignedat} \] ktorej riešením je \(x'=400\) a \(y'=0\). Podľa riešenia skladníka sa teda zdá, že druhá vakcína bola dodaná do skladu zadarmo, hoci v skutočnosti je takmer štyrikrát drahšia než prvá. Vypočítame relatívnu chybu a všetky hodnoty opäť uvedieme v tabuľke:
| vakcína | skutočná cena | skladníkov odhad ceny | relatívna chyba |
|---|---|---|---|
| Antiflu | \(250\,\text{Kč}\) | \(400\,\text{Kč}\) | \(\frac{400-250}{250}=60\,\%\) |
| Kontradift | \(900\,\text{Kč}\) | \(0\,\text{Kč}\) | \(\frac{900-0}{900}=100\,\%\) |
Úloha 3. Graficky znázornite sústavy rovníc z predchádzajúcich dvoch úloh pomocou vhodného softvéru. Vysvetlite rozdiel v presnosti výsledkov oboch úloh porovnaním ich grafov.
Riešenie. Nech \(p_1\), \(p_2\) (alebo \(q_1\), \(q_2\)) sú priamky dané rovnicami sústavy s nezaokrúhlenými koeficientmi v Úlohe 1 (alebo Úlohe 2), teda \[ \begin{aligned} p_1 &\colon 597x + 386 y = 401\,950 \\ p_2 &\colon 86x + 19 y = 39\,600 \\[2mm] q_1 &\colon 504x + 81 y = 198\,900 \\ q_2 &\colon 98x + 18 y = 40\,700. \end{aligned} \] Priamky dané príslušnými rovnicami so zaokrúhlenými koeficientmi označme \(p'_1\), \(p'_2\), \(q'_1\) a \(q'_2\) a ďalej označme priesečníky \(P\in p_1\cap p_2\), \(P'\in p'_1\cap p'_2\), \(Q\in q_1\cap q_2\) a \(Q'\in q'_1\cap q'_2\). Grafické znázornenie dvojice sústav pre každú úlohu samostatne je na nasledujúcom obrázku.
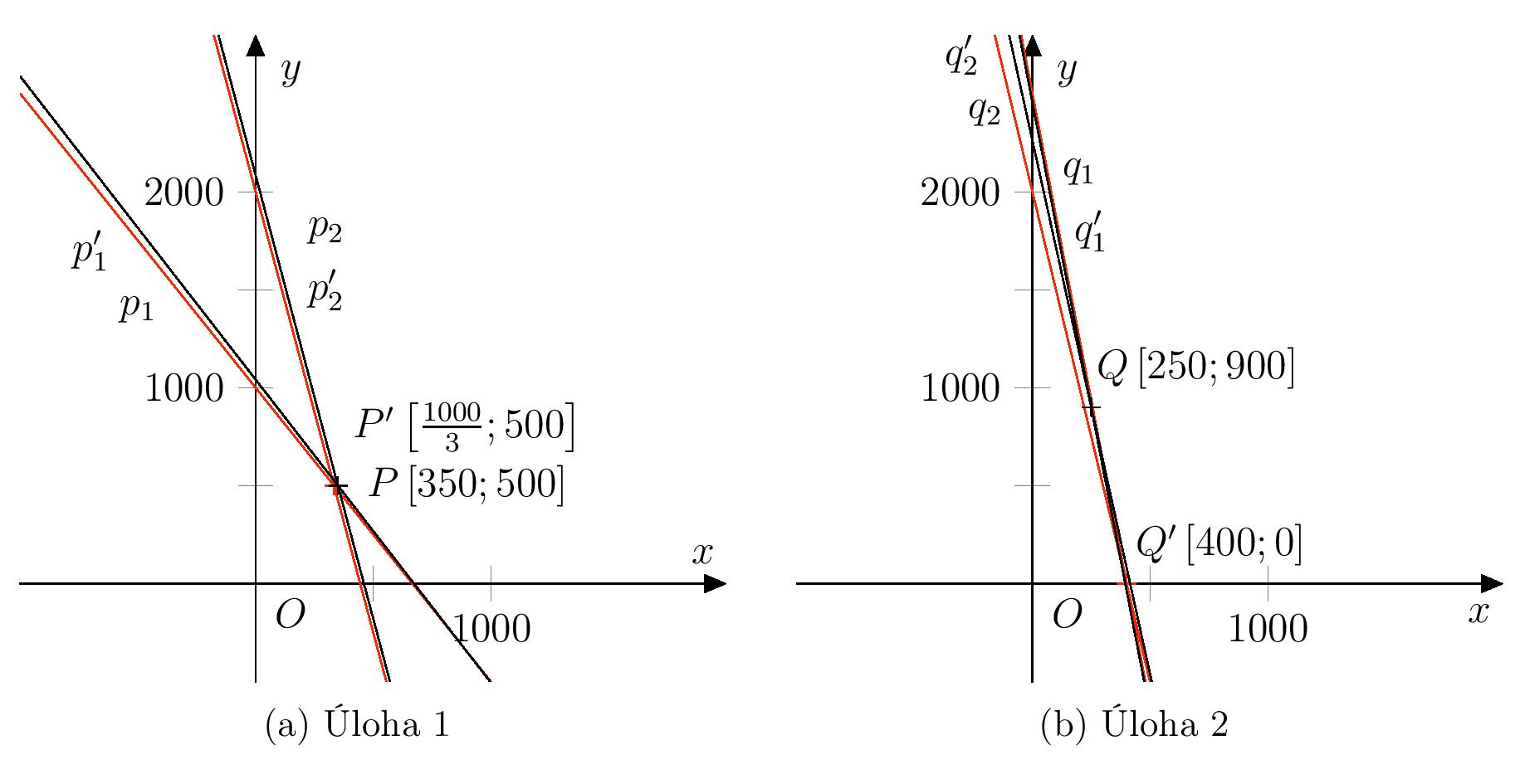
Porovnaním obidvoch grafických znázornení vidíme, že v prípade Úlohy 2 je dvojica priamok \(q_1\) a \(q_2\) takmer rovnobežná. Pri zaokrúhľovaní koeficientov rovnice sa poloha priamok voči súradnicovej sústave všeobecne mení a mení sa aj poloha priesečníka. Zmena polohy priesečníka je oveľa väčšia pri takmer rovnobežných priamkach. Obrázok tiež ukazuje, prečo je druhá súradnica priesečníka (t. j. cena vakcíny Kontradift) v druhej úlohe oveľa viac ovplyvnená zaokrúhľovaním. Vzhľadom na sklon priamok \(q_1\) a \(q_2\) malá zmena v \(x\)-ovej súradnici priesečníka znamená veľkú zmenu v jeho \(y\)-ovej súradnici.
Literatura
- Biermann K., Grötschel M., Lutz-Westphal B. (2010). Besser als Mathe: Moderne angewandte Mathematik aus dem MATHEON zum Mitmachen. Berlin: Vieweg+Teubner.