Ciekawski kierownik magazynu
 35 min.,
35 min.,  2/3
2/3 Kiedy rozwiązujemy problemy czysto matematyczne, otrzymujemy dokładne wyniki. Jednakże, gdy używamy matematyki do rozwiązywania problemów w otaczającym nas świecie, rzadko osiągamy absolutną precyzję odpowiedzi. Przybliżenie jest czasami wynikiem uproszczenia rzeczywistej sytuacji w naszych umysłach. Czasami dane wejściowe są przybliżone (np. możemy mierzyć długość lub czas z ograniczoną dokładnością) lub absolutnie dokładny wynik jest realistycznie nieosiągalny i musi zostać zaokrąglony.
Zaokrąglanie do określonej liczby cyfr znaczących jest często stosowane w praktyce (i w poniższych problemach). Zaokrąglamy dodatnią liczbę rzeczywistą \(r\) do \(n\) cyfr znaczących w następujący sposób:
- Wyrażamy \(r\) w postaci \(a\cdot 10^b\) , gdzie \(a\in\mathbb{R}\), \(a\in\left\langle 1,10 \right)\) i \(b\in\mathbb{Z}\) , a następnie zaokrąglamy liczbę \(a\) do \(n-1\) miejsc po przecinku zgodnie ze standardowymi zasadami zaokrąglania.
- Np. liczby \(r=31{.}258\,16\) i \(s=0{.}023 \,123\,6\) zaokrąglamy do czterech prawidłowych cyfr w następujący sposób:
\[ \begin{aligned} r &= 31{.}258\,16 = 3{.}125\,816 \cdot 10^1 \quad \doteq\quad 3{.}126 \cdot 10^1 = 31{.}26 \\ s &= 0{.}023 \,123\,6 = 2{.}312\,36 \cdot 10^{-2} \quad \doteq\quad 2{.}312 \cdot 10^{-2} = 0{.}023\,12. \end{aligned} \]
Warto zauważyć, że zaokrąglanie danych wejściowych może mieć zaskakujące konsekwencje dla dokładności wyniku, na przykład podczas rozwiązywania równań, o czym przekonamy się w poniższej serii problemów.
Ćwiczenie 1. Kierownik hurtowni farmaceutycznej otrzymał fakturę za dwa rodzaje zamówionych szczepionek. Łącznie \(401{,}950\,\text{CZK}\) zapłacono za dostarczenie opakowań szczepionek Ixodinum przeciwko zapaleniu mózgu o wartości 597 USD oraz 386 opakowań szczepionek Nopolio przeciwko polio. Jednak podczas wstępnej inspekcji, opakowania szczepionki Ixodinum o wartości 86 USD i opakowania szczepionki Nopolio o wartości 19 USD okazały się przeterminowane i musiały zostać zwrócone. Łącznie zwrócono kwotę \(39{,}600\,\text{CZK}\) za przeterminowane leki.
Z ciekawości kierownik chce obliczyć cenę zakupu jednego opakowania obu szczepionek. Nie ma jednak pod ręką kalkulatora ani telefonu komórkowego, więc decyduje się na rozwiązanie przybliżone. Zaokrągla wszystkie znane mu liczby do jednej cyfry znaczącej przed wykonaniem obliczeń.
Jak bardzo jego wynik będzie się różnił od rzeczywistej ceny zakupu? Dla obu rodzajów szczepionek określ bezwzględną różnicę między cenami rzeczywistymi, a także błąd względny wyrażony w procentach.
Rozwiązanie. Najpierw rozwiążmy problem bez zaokrąglania. Niech \(x\) będzie ceną za opakowanie Ixodine, a \(y\) ceną za opakowanie Nopolio. Informacje zawarte w zadaniu prowadzą do układu dwóch równań liniowych z dwiema niewiadomymi
\[ \begin{alignat*}{2} 597x &\,+& 386 y &= 401{,}950 \\ 86x &\,+& 19 y &= 39{,}600 \end{alignat*} \]
którego rozwiązanie daje nam rzeczywistą cenę zakupu opakowania szczepionki Ixodin \(350\,\text{CZK}\) oraz opakowania szczepionki Nopolio \(500\,\text{CZK}\).
Po zaokrągleniu współczynników do jednej cyfry znaczącej, rozwiązujemy układ
\[ \begin{alignat*}{2} 600x' &\,+ & 400 y' &= 400\,000 \\ 90x' &\,+ & 20 y' &= 40\,000. \end{alignat*} \]
Rozwiązaniem jest para \(x'=\frac{1{,}000}{3}\doteq333\) i \(y'=500\). Teraz mamy rzeczywistą cenę leku i szacunkową cenę podaną przez kierownika magazynu. Obliczmy również błąd względny w cenie leku wynikający z zaokrąglenia. Błąd względny to błąd bezwzględny (bezwzględna wartość różnicy w cenie) podzielona przez rzeczywistą cenę za opakowanie. Wyniki podsumowujemy w tabeli:
| szczepionka | cena rzeczywista | cena szacunkowa | błąd względny |
|---|---|---|---|
| Ixodinum | \(350\,\text{Kč}\) | \(333\,\text{Kč}\) | \(\frac{350-333}{350}=4{,}9\,\%\) |
| Nopolio | \(500\,\text{Kč}\) | \(500\,\text{Kč}\) | \(\frac{500-500}{500}=0\,\%\) |
Ćwiczenie 2. Po kilku miesiącach do magazynu dotarła kolejna dostawa, a mianowicie \(504\) opakowań szczepionek Antiflu przeciwko grypie po 81 dolarów za opakowania szczepionek Kontradift przeciwko błonicy. Kwota \(198{,}900\,\text{CZK}\) została zapłacona za tę dostawę. Podczas wstępnej kontroli, opakowania Antiflu o wartości 98 USD i opakowania Contradift o wartości 18 USD okazały się przeterminowane. Łącznie \(40{,}700\,\text{CZK}\) została zwrócona.
Kierownik magazynu powtórzył swoją procedurę i obliczył przybliżoną cenę zakupu obu leków. Tym razem jednak był zaskoczony. Jaki był powód jego zaskoczenia i jak bardzo jego wynik różnił się od rzeczywistych cen?
Rozwiązanie. Rozwiążemy problem w taki sam sposób jak poprzednio, tym razem oznaczymy \(x\) jako cenę jednego opakowania Antiflu a \(y\) cenę jednego opakowania Contradift. Rzeczywiste ceny są rozwiązaniem układu
\[ \begin{alignat*}{2} 504x &\,+\,& 81 y &= 198{,}900 \\ 98x &\,+\,& 18 y &= 40{,}700 \end{alignat*} \]
gdzie otrzymujemy \(x=250\) i \(y=900\).
Po zaokrągleniu współczynników rozwiązujemy układ
\[ \begin{alignat*}{2} 500x' &\,+\,& 80 y' &= 200{,}000 \\ 100x' &\,+\,& 20 y' &= 40{,}000, \end{alignat*} \]
którego rozwiązaniem jest \(x'=400\) i \(y'=0\). Z rozwiązania kierownika magazynu wynika, że druga szczepionka została dostarczona do magazynu bezpłatnie, podczas gdy w rzeczywistości jest ona prawie cztery razy droższa niż pierwsza. Obliczamy błąd względny i ponownie wpisujemy wszystkie wartości do tabeli:
| szczepionka | cena rzeczywista | cena szacunkowa | błąd względny |
|---|---|---|---|
| Antiflu | \(250\,\text{Kč}\) | \(400\,\text{Kč}\) | \(\frac{400-250}{250}=60\,\%\) |
| Kontradift | \(900\,\text{Kč}\) | \(0\,\text{Kč}\) | \(\frac{900-0}{900}=100\,\%\) |
Ćwiczenie 3. Przedstaw graficznie układy równań z poprzednich dwóch zadań przy użyciu odpowiedniego oprogramowania. Wyjaśnij różnicę w dokładności wyników obu ćwiczeń porównując ich wykresy.
Rozwiązanie. Niech \(p_1\), \(p_2\) (or \(q_1\), \(q_2\)) będą liniami wyznaczonymi przez równania układu o niezaokrąglonych współczynnikach w Ćwiczeniu 1 (lub Ćwiczeniu 2), a mianowicie
\[ \begin{align*} p_1 &\colon 597x + 386 y = 401{,}950 \\ p_2 &\colon 86x + 19 y = 39{,}600 \\[2mm] q_1 &\colon 504x + 81 y = 198{,}900 \\ q_2 &\colon 98x + 18 y = 40{,}700. \end{align*} \]
Oznaczmy linie wyznaczone przez odpowiednie równania z zaokrąglonymi współczynnikami przez \(p'_1\), \(p'_2\), \(q'_1\) i \(q'_2\) i dalej oznaczają punkty \(P\in p_1\cap p_2\), \(P'\in p'_1\cap p'_2\), \(Q\in q_1\cap q_2\) and \(Q'\in q'_1\cap q'_2\). Graficzną reprezentację pary systemów dla każdego problemu z osobna przedstawiono na poniższym rysunku.
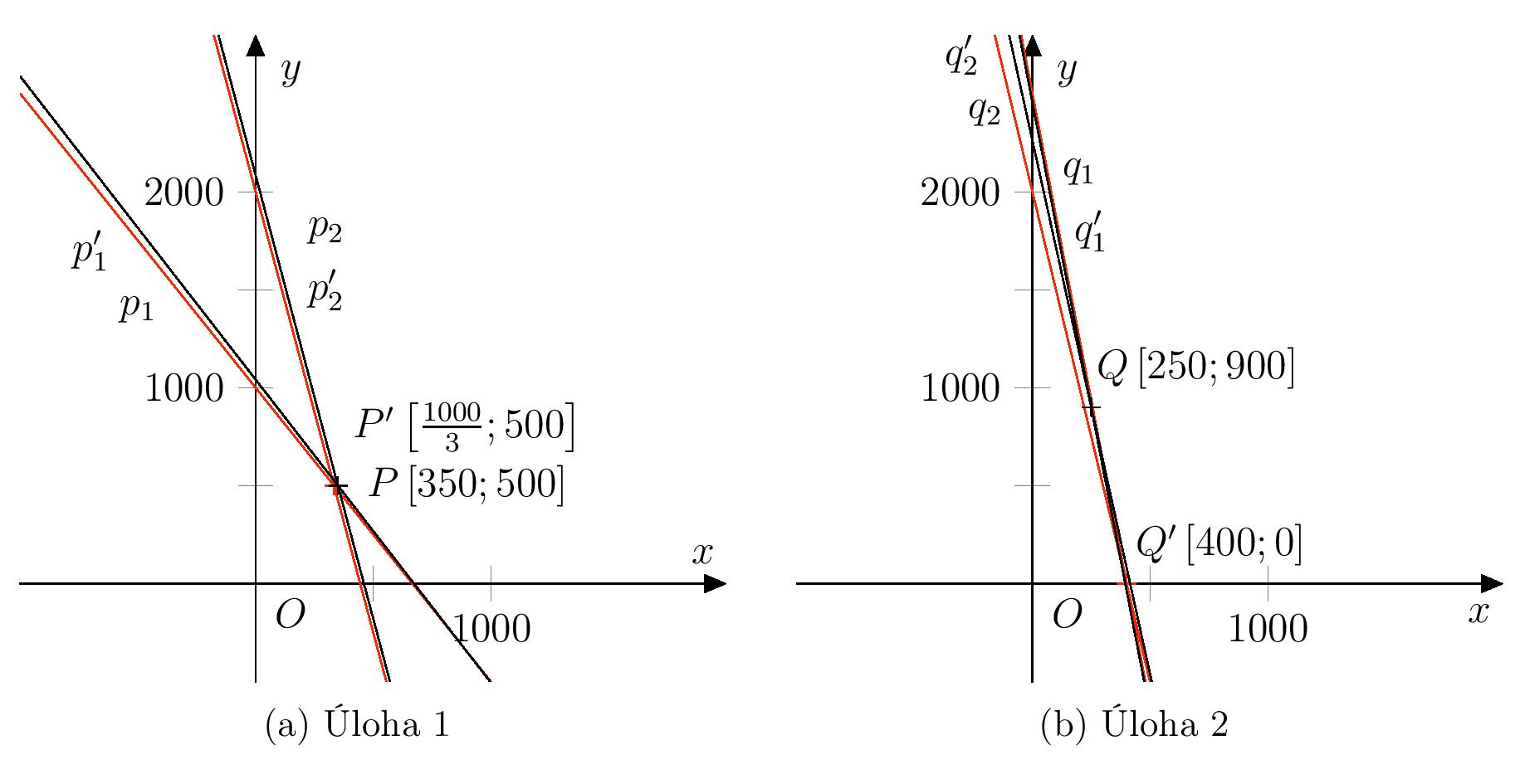
Porównując dwie reprezentacje graficzne, można zauważyć, że w przypadku ćwiczenia 2, linie \(q_1\) i \(q_2\) są prawie równoległe. Podczas zaokrąglania współczynników równania, położenie linii względem układu współrzędnych generalnie się zmienia i zmienia się również położenie punktu przecięcia. Zmiana położenia punktu przecięcia jest znacznie większa dla linii, które są prawie równoległe. Rysunek pokazuje również, dlaczego druga współrzędna punktu przecięcia (tj. cena szczepionki Contradift) będzie miała znacznie większy wpływ na zaokrąglenie w drugim problemie. Ze względu na nachylenie linii \(q_1\) i \(q_2\), niewielka zmiana współrzędnej \(x\) przecięcia oznaczałaby dużą zmianę współrzędnej \(y\).
Literatura
- Biermann K., Grötschel M., Lutz-Westphal B. (2010). Lepsze niż matematyka: Nowoczesna matematyka stosowana od MATHEON do przyłączenia się. Berlin: Vieweg+Teubner.