Cień domu
 40 min.,
40 min.,  3/3
3/3 Martin chce przygotować miejsce na płótnie, aby narysować dom w słoneczny dzień. Dlatego zwizualizował prosty model domu w rzucie równoległym (ortograficznym), stojąc na poziomym płaskim podłożu. Dom ma kształt prostopadłościanu z prostym czterospadowym dachem. Dach biodrowy to dach utworzony przez dwa trójkąty równoramienne i dwa trójkąty prostokątne. trapez równoramienny. Wszystkie cztery płaszczyzny dachu mają takie samo nachylenie. Na płótnie obok domu umieścił pionowy pręt i jego cień (patrz rysunek).
Aby opisać rozwiązanie, będziemy potrzebować następujących terminów:
- Cień własny obiektu to nieoświetlona część jego powierzchni. Zamknięta linia na powierzchni obiektu, która oddziela świecące elementy a nieoświetlone części nazywane są granicą cienia jaźni.
- Cień rzucany obiektu jest jego projekcją. w kierunku promieni świetlnych na daną płaszczyznę. Stwierdza on, że granicą rzucanego cienia jest rzucany cień. granicy własnego cienia
Zadanie 1. Zaznacz na rysunku własny cień domu i cień domu rzucany na ziemię przez słońce. (Odległość od Słońca do powierzchni Ziemi jest tak duża, że możemy uznać promienie słoneczne za równoległe do siebie). 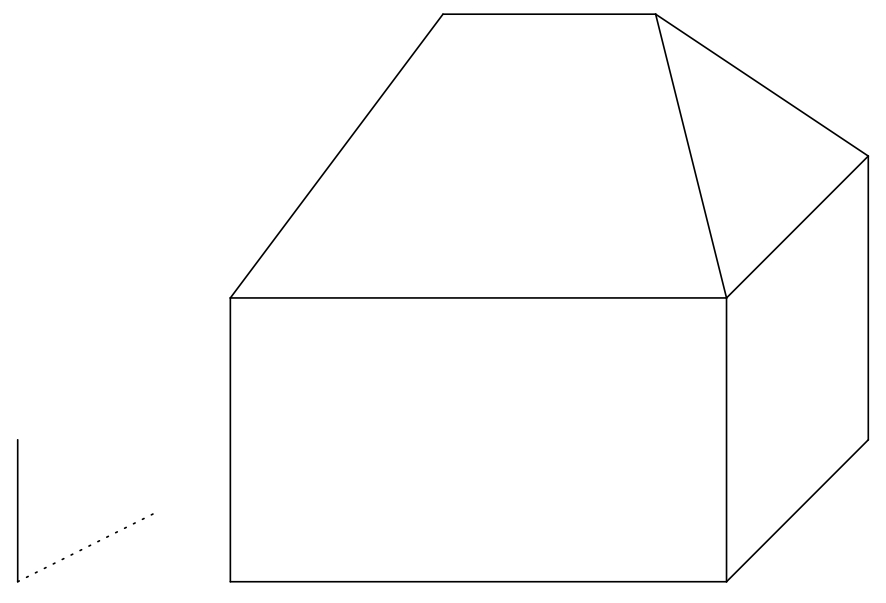
Rozwiązanie. Niech \(P\) oznacza podstawę pręta, \(Q\) jego górny koniec, a \(R\) cień rzucany przez punkt \(Q\). Zorientowany segment \(QR\) określa zatem kierunek i orientację promieni świetlnych. Linia \(PR\) jest rzutem prostopadłym linii \(QR\) na płaszczyznę podłoża. W dalszej części tekstu oznaczymy płaszczyznę podłoża przez \(\pi\). Następnie oznaczmy wierzchołki prostopadłościanu \(ABCDEFGH\) i punkty końcowe kalenicy dachu przez \(S\) i \(T\).
Oświetlona część domu obejmuje lewą i przednią stronę prostopadłościanu i odpowiadających mu części dachu. Granicą cienia własnego jest zatem zamknięty wielokątny łańcuch \(ABFTSHDA\). Aby określić granicę cienia rzucanego przez dom, wystarczy skonstruować cienie rzucane na wierzchołki tego wielokątnego łańcucha. Spośród nich \(A\), \(B\) i \(D\) leżą już w płaszczyźnie \(\pi\) i dlatego o również są swoimi własnymi cieniami. Dlatego, wystarczy skonstruować cienie punktów \(F\), \(T\), \(S\) i \(H\). Cień rzucany przez punkt \(T\) jest przecięciem promienia świetlnego przechodzący przez nią z rzutem prostopadłym tego promienia na płaszczyznę \(\pi\). Przypomnijmy, że kierunek promieni świetlnych to wyznaczony przez linię \(QR\) i kierunek linii \(QR\). Rzut prostopadły promieni na płaszczyznę \(\pi\) wynosi określony przez linię \(PR\). Prostopadły rzut promienia przechodzi dalej przez punkt \(T_1\), który jest rzutem prostopadłym punktu \(T\) na płaszczyznę \(\pi\). Jeśli oznaczymy cień rzucany przez punkt \(T\) jako \(T'\), jego konstrukcja jest pokazana na rysunku.
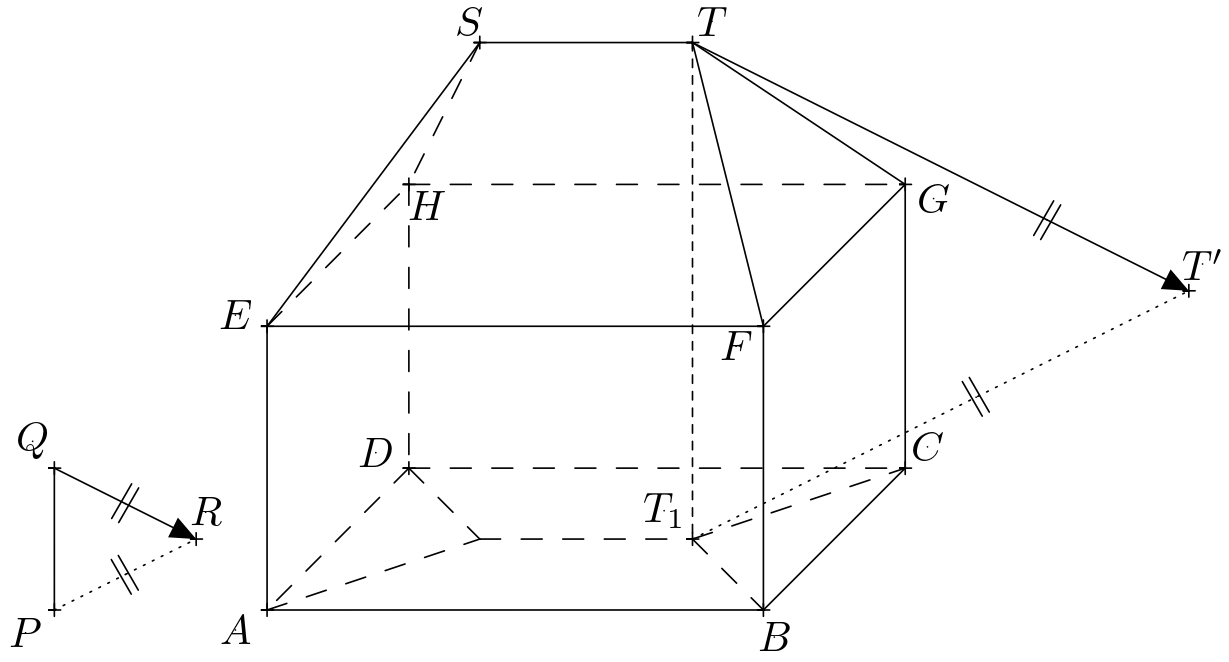
Konstruujemy cienie rzutowane \(F'\), \(S'\), \(H'\) punktów \(F\), \(S\), i \(H\) podobnie. Granicą cienia rzucanego przez dom jest wtedy wielokąt \(ABF'T'S'H'D\). Podczas cieniowania bierzemy pod uwagę tylko widoczne części siebie i rzucane cienie.
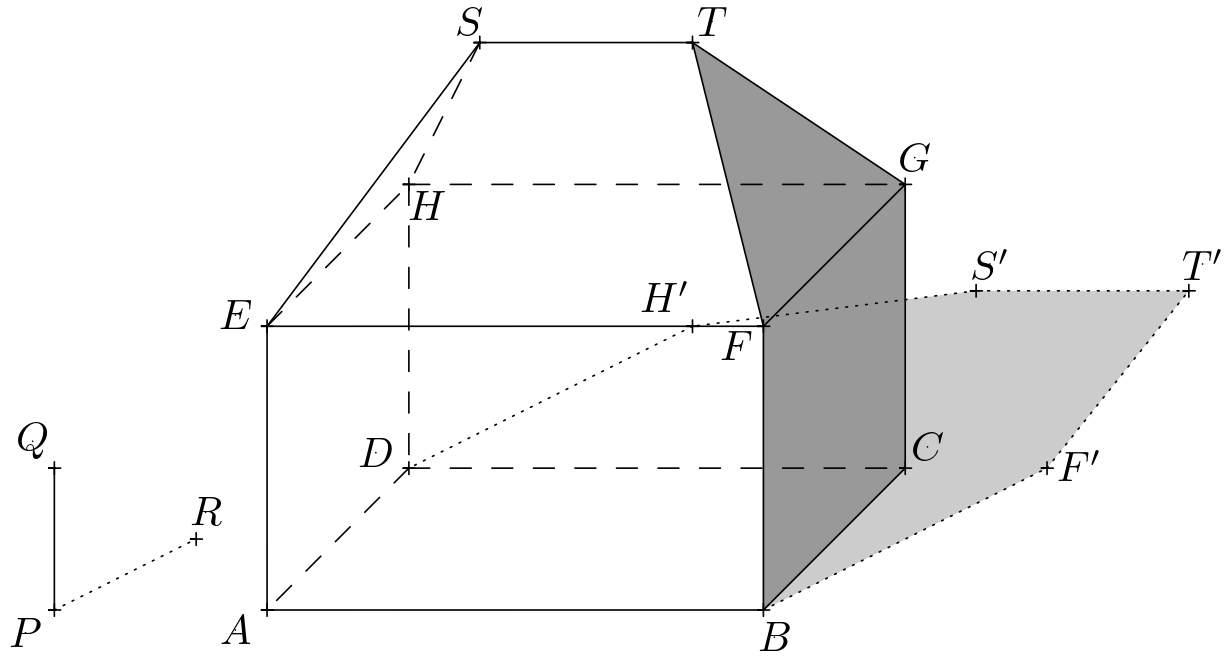
Zadanie 2. Narysuj cień rzucany przez dom, jeśli istnieje nieprzezroczysta ściana za domem, która jest równoległa do frontu i tylnej ściany domu. 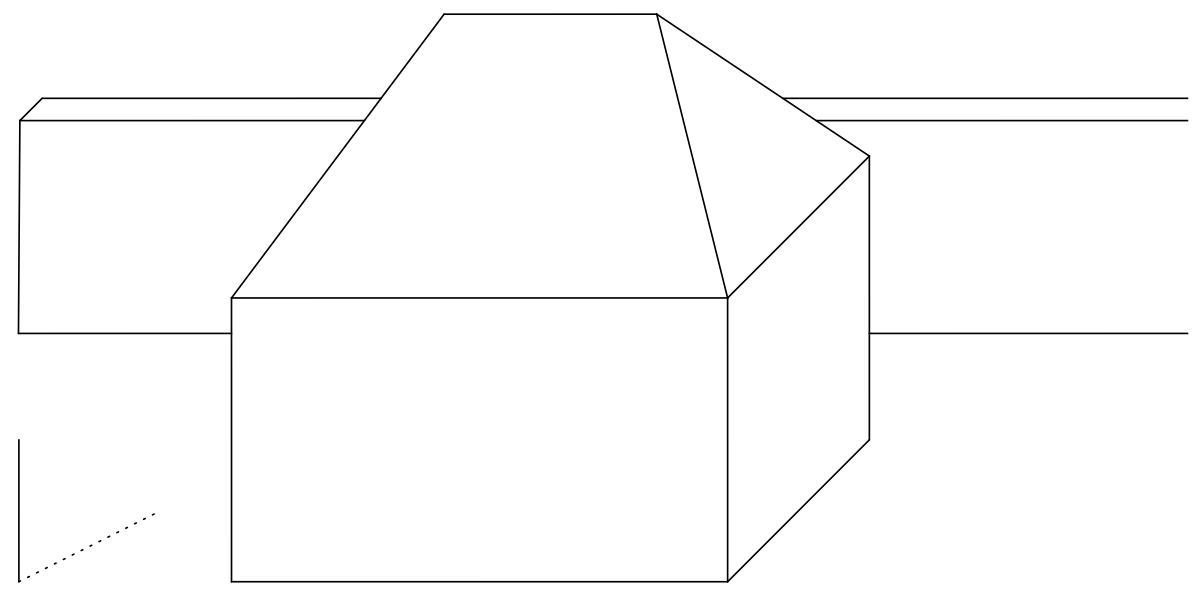
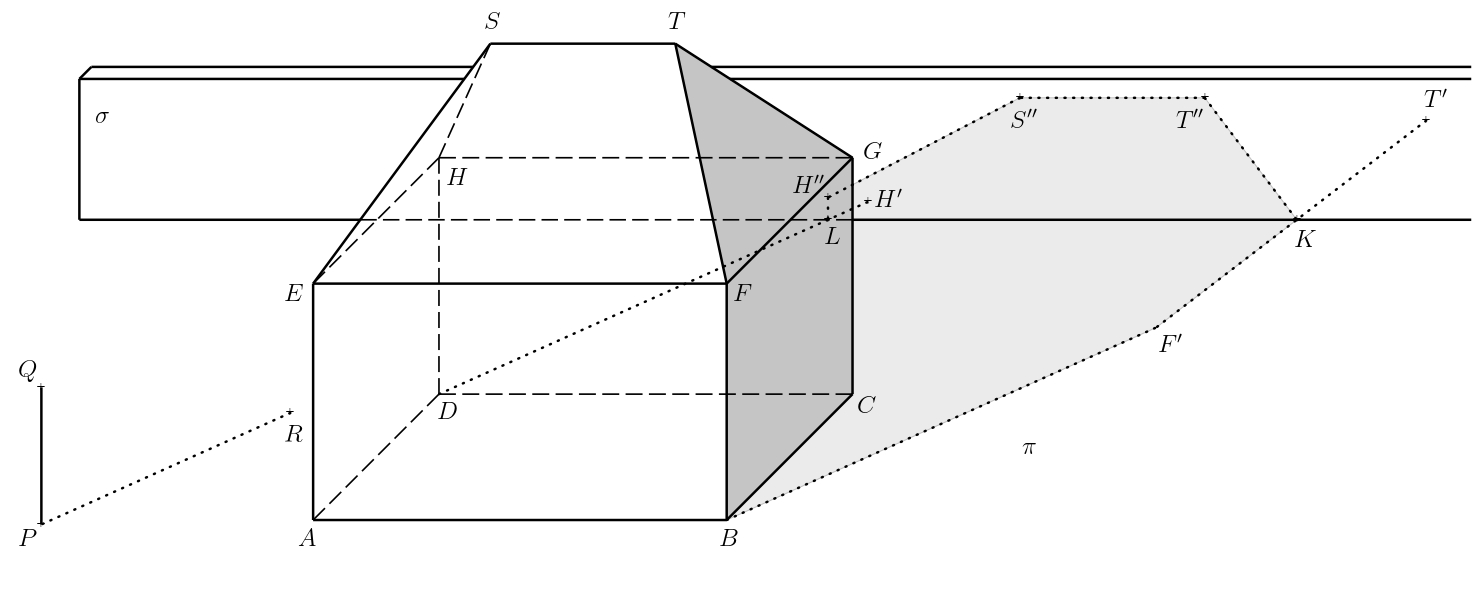
Rozwiązanie. Cień własny domu, jego granica i rzucane cienie do płaszczyzny \(\pi\), które z naszej perspektywy znajdują się przed ścianą, pozostają niezmienione. Oznaczmy przez \(\sigma\) płaszczyznę, w której leży przednia strona dodanej ściany. Dla punktów \(T\), \(S\) i \(H\), konieczne jest, aby tworzyły swoje cienie rzucane na tę płaszczyznę. Opiszmy to dla punktu \(T\).
Rozważmy punkty \(T_1\) i \(T'\) z poprzedniego ćwiczenia. Niech \(\tau\) oznacza płaszczyznę \(TT_1T'\), a dalej oznaczmy przez \(U\) przecięcie linii \(T_1T'\) a dolną krawędzią ściany (tj. \(\sigma\cap\pi\)).
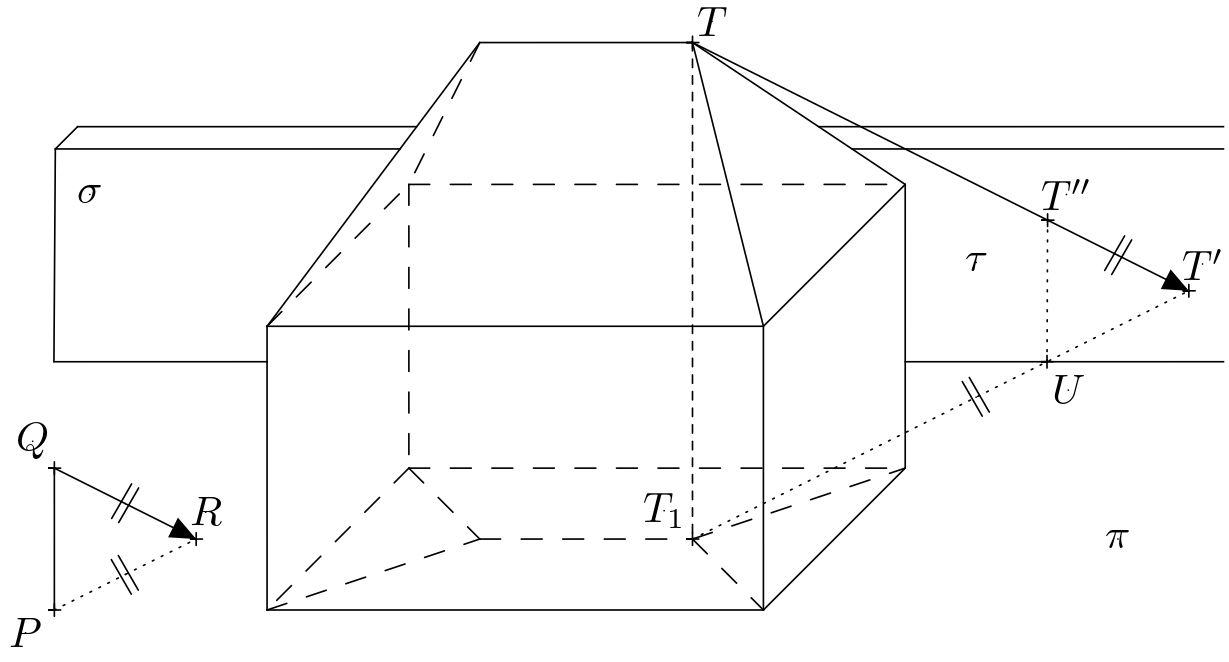
Przecięcie płaszczyzn \(\sigma\) i \(\tau\) również musi przechodzić przez ten punkt, tj. cień \(T_1T\) rzucany na punkt w płaszczyźnie \(\sigma\). Co więcej, to przecięcie musi być pionowe, ponieważ zarówno \(\tau\), jak i \(\sigma\) są pionowe. Cień rzucany przez punkt \(T\) na płaszczyznę \(\sigma\) (oznaczmy go przez \(T''\)) leży na wspomnianym przecięciu i linii \(TT'\).
Konstruujemy cienie rzutowane \(S''\), \(H''\) punktów \(S\) i \(H\). Granicą własnego cienia jest wtedy zamknięty wielokątny \(ABF'KT''S''H''LDA\), gdzie \(K\) (resp. \(L\)) leży na przecięciu płaszczyzn \(\sigma\) i \(\pi\), a także leży na \(F'T'\) (odpowiednio \(DH'\)). Zacieniamy tylko widoczne części jaźni i rzucane cienie, nie zacieniamy części cienia zasłoniętego przez dom.
Uwaga. W celu lepszej wizualizacji pomocny może być również interaktywny aplet w programie GeoGebra. W aplecie można do pewnego stopnia modyfikować kierunek promieni słonecznych, zob.https://www.geogebra.org/m/ecyqv4qg
Zadanie 3. Zaznacz na rysunku własny cień domu i cień domu rzucany na ziemię przez słońce. (Odległość od Słońca do powierzchni Ziemi jest tak duża, że możemy uznać promienie słoneczne za równoległe do siebie). 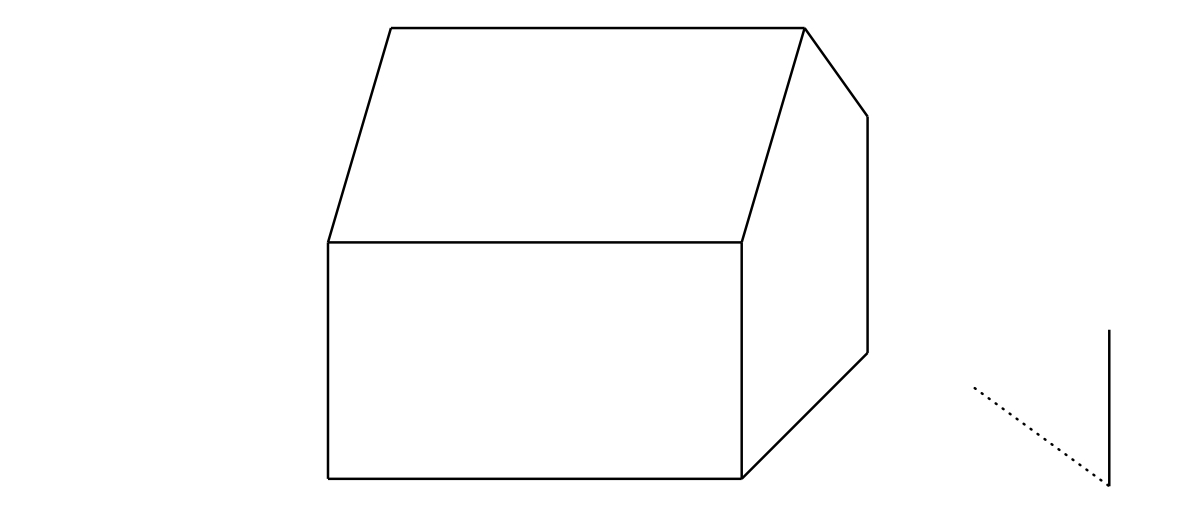
Rozwiązanie.
Literatura
- Pomykalová E. Deskriptivní geometrie pro střední školy. Prometheus. 2010. 106—107.