Stín domu
 40 min.,
40 min.,  3/3
3/3 Martin si chce rozvrhnout místo na plátně, aby mohl nakreslit dům za slunečného dne. Znázornil si proto ve volném rovnoběžném promítání jednoduchý model domu, který stojí na vodorovném pozemku, tvořený kvádrem s jednoduchou valbovou střechou. Valbová střecha je střecha domu tvořená dvěma rovnoramennými trojúhelníky a dvěma rovnoramennými lichoběžníky. Všechny čtyři střešní roviny mají stejný spád. Na plátně dále vedle domku umístil svislou tyč a její stín (viz obrázek).
Pro popis řešení budeme potřebovat následující pojmy:
- Vlastní stín objektu je neosvětlená část povrchu objektu. Uzavřená čára na povrchu objektu, která odděluje osvětlenou a neosvětlenou část, se nazývá hranice vlastního stínu.
- Vržený stín objektu je průmět objektu ve směru světelných paprsků do dané roviny. Platí, že hranice vrženého stínu je vržený stín hranice stínu vlastního
Úloha 1. Vyznačte v obrázku vlastní stín domu a stín vržený na zem Sluncem. Vzdálenost Slunce od povrchu Země je tak velká, že sluneční paprsky můžeme považovat za navzájem rovnoběžné.
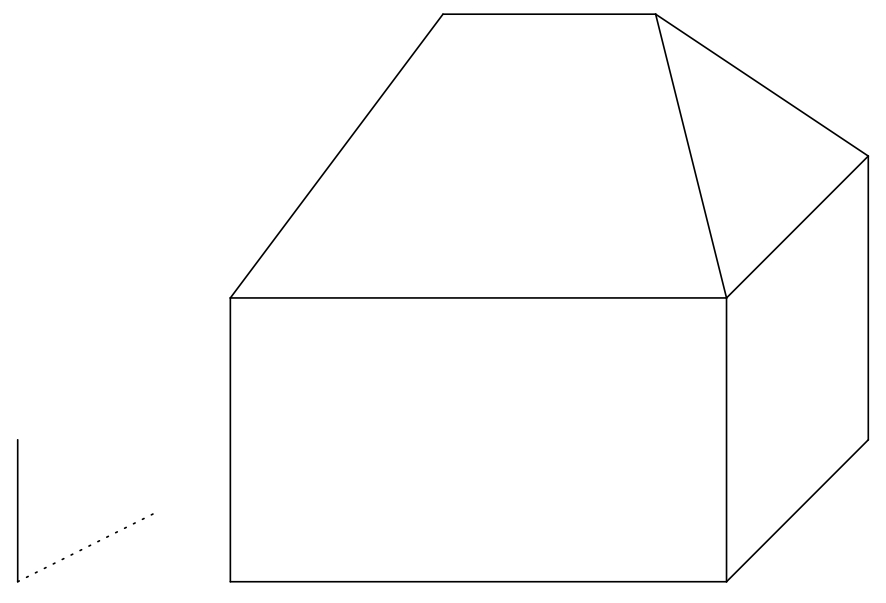
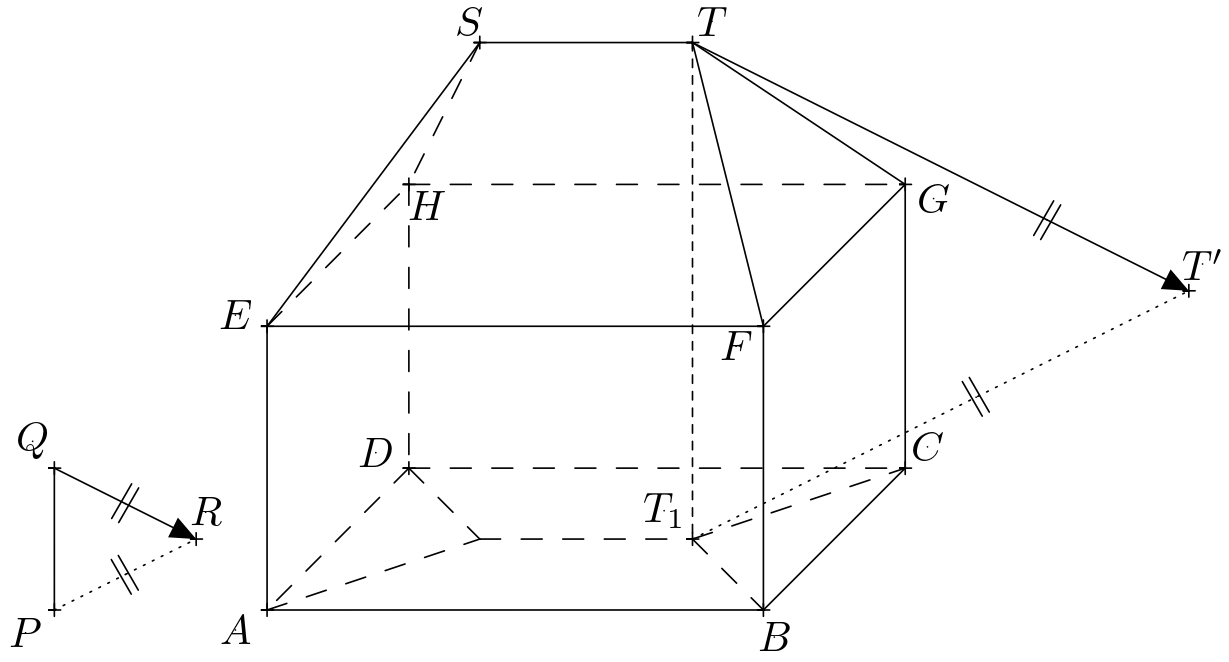
Řešení. Označme \(P\) patu tyče, \(Q\) její horní konec a \(R\) vržený stín bodu \(Q\). Orientovaná úsečka \(QR\) tak určuje směr a orientaci světelných paprsků, přímka \(PR\) je pravoúhlý průmět přímky \(QR\) do roviny země. Tu budeme v dalším textu označovat \(\pi\). Označme dále vrcholy kvádru \(ABCDEFGH\) a koncové body hřebene střechy označme \(S\) a \(T\).
Osvětlenou částí domu jsou levá boční a přední stěna kvádru a příslušné části střechy. Hranicí vlastního stínu je tak uzavřená lomená čára \(ABFTSHDA\). K určení hranice vrženého stínu domu tak stačí sestrojit vržené stíny vrcholů této lomené čáry. Z nich \(A\), \(B\) a \(D\) již v rovině \(\pi\) leží a jsou tedy zároveň vlastními vrženými stíny. Stačí proto sestrojit vržené stíny bodů \(F\), \(T\), \(S\) a \(H\).
Vržený stín bodu \(T\) je průsečíkem světelného paprsku, který jím prochází, s kolmým průmětem tohoto paprsku do roviny \(\pi\). Připomeňme, že směr světelných paprsků je určen přímkou \(QR\) a směr kolmého průmětu paprsků do roviny \(\pi\) je určen přímkou \(PR\). Kolmý průmět paprsku dále prochází bodem \(T_1\), který je kolmým průmětem bodu \(T\) do roviny \(\pi\). Označíme-li vržený stín bodu \(T\) jako \(T'\), jeho konstrukci znázorňuje obrázek.
Obdobně sestrojíme i vržené stíny \(F'\), \(S'\), \(H'\) bodů \(F\), \(S\) a \(H\). Hranicí vrženého stínu domu je pak mnohoúhelník \(ABF'T'S'H'D\). Při stínování dále zohledníme viditelné části vlastního i vrženého stínu.
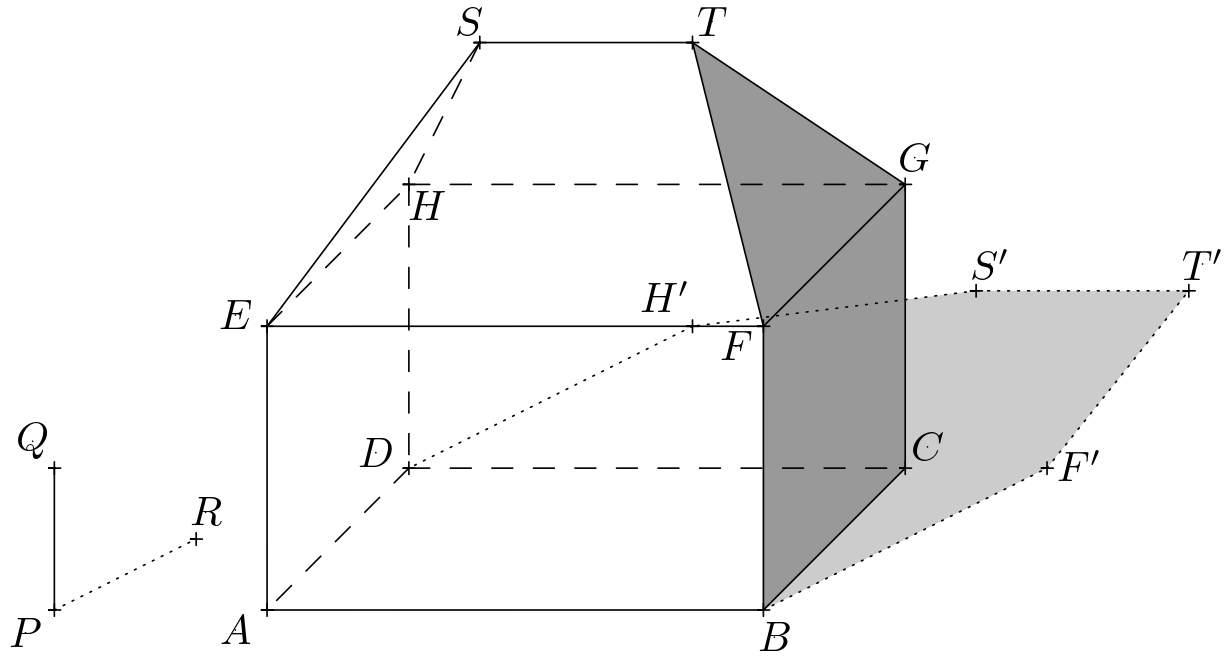
Úloha 2. Narýsujte vržený stín domu, je-li za domem přítomná neprůhledná zeď, která je rovnoběžná s přední a zadní stěnou domu.
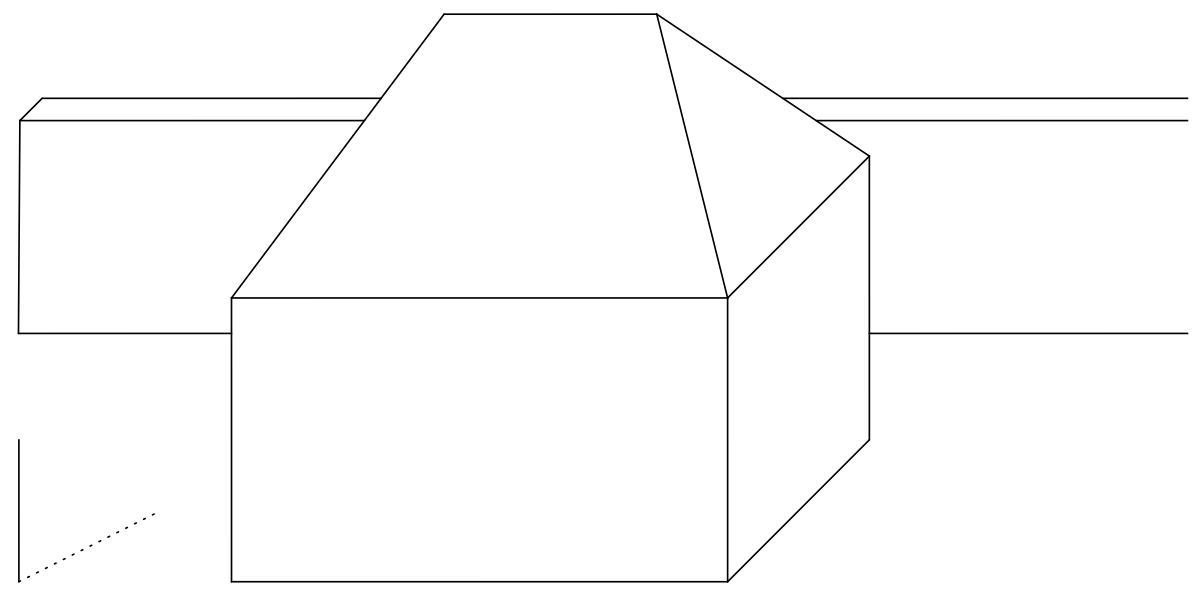
Řešení. Vlastní stín domu, jeho hranice a vržené stíny bodů do roviny \(\pi\), které se nachází z našeho pohledu před zdí, zůstanou nezměněny. Označme \(\sigma\) rovinu, ve které leží přední stěna přidané zdi. Pro trojici bodů \(T\), \(S\) a \(H\) je třeba sestrojit jejich vržené stíny do této roviny. Blíže popíšeme konstrukci opět jen pro bod \(T\).
Uvažme body \(T_1\) a \(T'\) z minulé úlohy. Označme \(\tau\) rovinu \(TT_1T'\) a dále označme \(U\) průsečík přímky \(T_1T'\) a spodní hrany zdi (tj. \(\sigma\cap\pi\)).
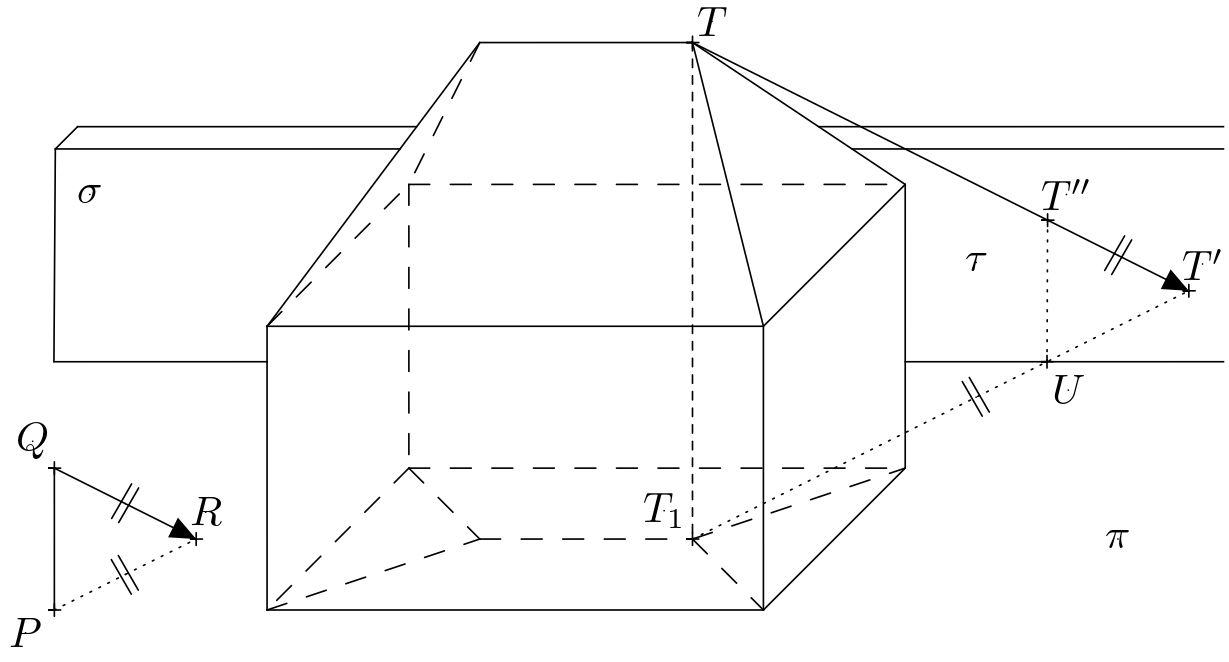
Tímto bodem musí procházet i průsečnice rovin \(\sigma\) a \(\tau\), tj. stín \(T_1T\) vržený do roviny \(\sigma\). Tato průsečnice navíc musí být svislá, protože \(\tau\) i \(\sigma\) jsou svislé. Vržený stín bodu \(T\) do roviny \(\sigma\) (označme jej \(T''\)) pak leží na řečené průsečnici a přímce \(TT'\).
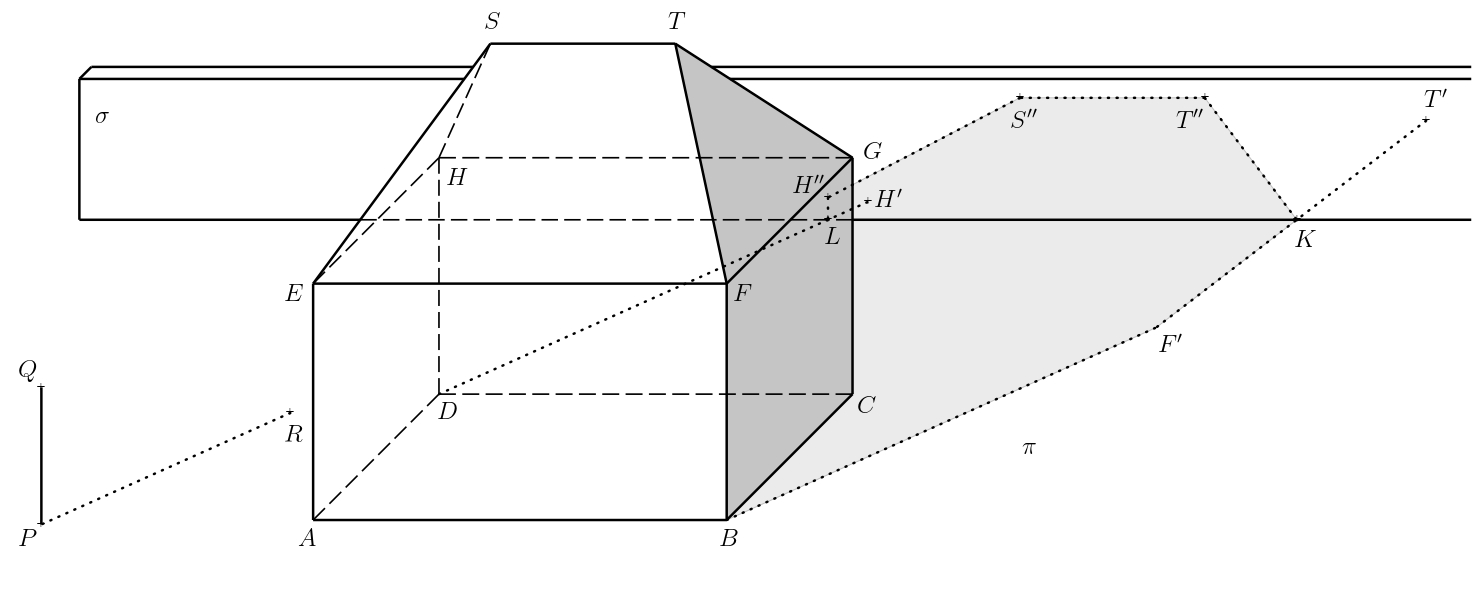
Podobně sestrojíme i vržené stíny \(S''\), \(H''\) bodů \(S\) a \(H\). Hranicí vlastního stínu je pak uzavřená lomená čára \(ABF'KT''S''H''LDA\), kde \(K\) (resp. \(L\)) leží na průsečnici rovin \(\sigma\) a \(\pi\) a dále leží na úsečce \(F'T'\) (resp. \(DH'\)). Stínujeme pouze viditelné části vlastního i vrženého stínu, části stínu zakryté domem nestínujeme.
Poznámka. Pro lepší představu může pomoci také interaktivní applet v GeoGebře, kde je možné směr slunečních paprsků omezeně měnit, viz https://www.geogebra.org/m/ecyqv4qg
Úloha 3. Vyznačte v obrázku vlastní stín domu a stín vržený na zem Sluncem. Vzdálenost Slunce od povrchu Země je tak velká, že sluneční paprsky můžeme považovat za navzájem rovnoběžné.
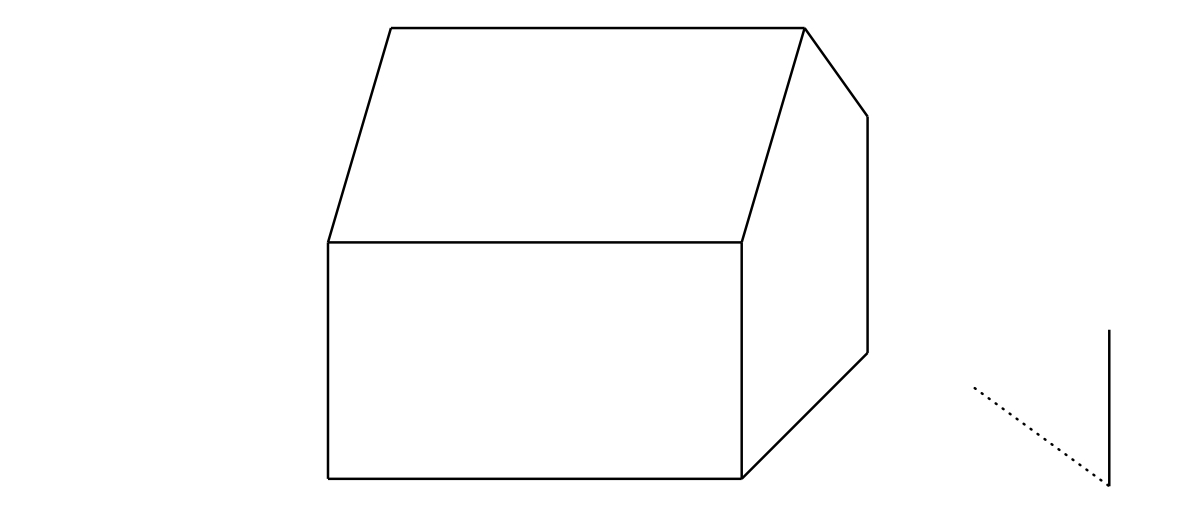
Řešení.
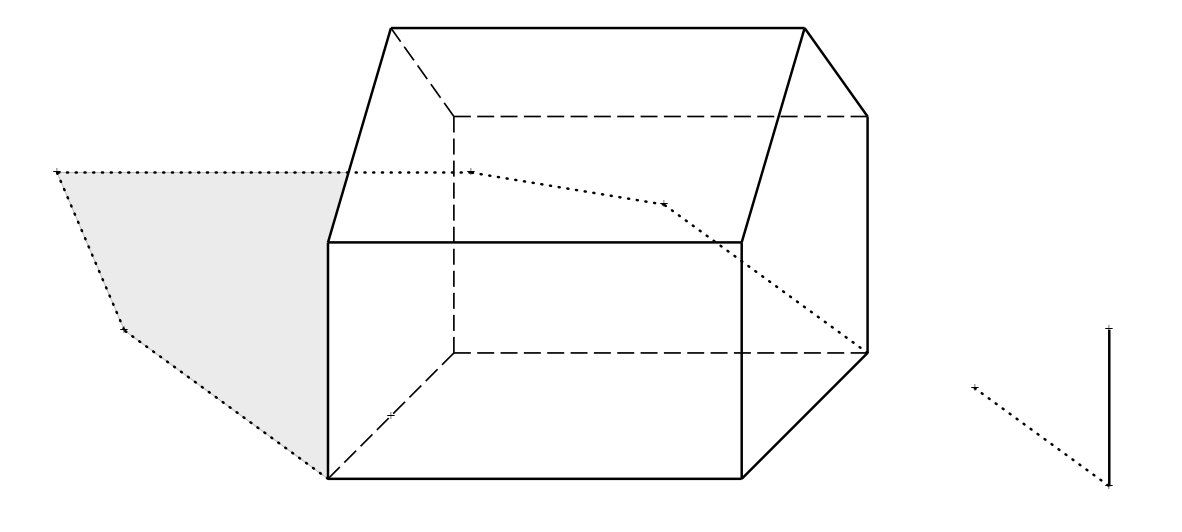
Literatura
- Pomykalová E. Deskriptivní geometrie pro střední školy. Prometheus. 2010. 106—107.