Postęp w dziedzinie inżynierii elektrycznej umożliwił opracowanie nowych systemów nawigacji opartych na transmisji fal elektromagnetycznych. Przykładem takiego systemu jest nawigacja morska LORAN-C, która została opracowana podczas II wojny światowej w USA. W tym typie nawigacji, statek odbiera zsynchronizowany sygnał z pary nadajników. Sygnał z bardziej oddalonego nadajnika jest odbierany przez statek później, więc opóźnienie sygnału określa różnicę między odległościami statku od pierwszego i drugiego nadajnika.
Zbiór punktów, które mają stałą różnicę odległości od dwóch punktów stałych jest hiperbolą. Zatem statek znajduje się na hiperboli, której ogniskami są nadajniki i która jest określona przez różnicę odległości statku od tych nadajników. Opóźnienie sygnału z innej pary stacji określa następnie drugą hiperbolę, na której musi znajdować się statek. Jeśli statek leży na obu hiperbolach, to leży na ich przecięciu.
Zadanie 1. Trzy odbiorniki \(P_1\), \(P_2\) i \(P_3\) są rozmieszczone w terenie. Rysunek przedstawia znane nam odległości: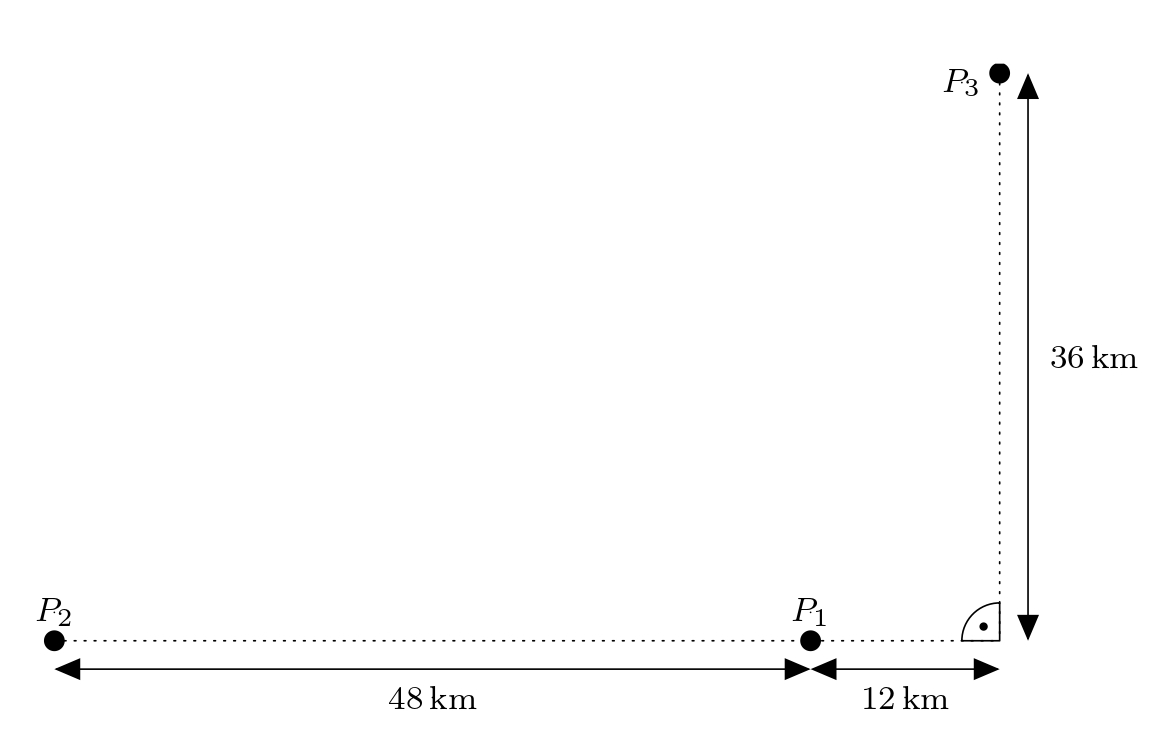 
Nawigacja turystyczna Adama wyśle sygnał do wszystkich trzech odbiorników. Sygnał dociera do odbiorników \(P_1\) i \(P_3\) w tym samym czasie, a do odbiornika \(P_2\) 80 mikrosekund później. Gdzie znajduje się Adam? Załóżmy, że sygnał pokonuje 300 000 km na sekundę. Określ pozycji w odpowiednio ustalonym układzie współrzędnych.
Rozwiązanie.Najpierw na rysunku wybieramy odpowiedni kartezjański układ współrzędnych. Uzasadniamy ten wybór w następujący sposób: Ponieważ Adam znajduje się w równej odległości od odbiorników \(P_1\) i \(P_3\), jest on umieszczony na osi linii \(P_1P_3\). Fakt, że jego sygnał dociera do odbiornika \(P_2\) 80 mikrosekund później niż do odbiornika \(P_1\) oznacza, że Adam znajduje się \(24\,\text{km}\) dalej od odbiornika \(P_2\) niż od odbiornika \(P_1\). Jego pozycja znajduje się zatem również na gałęzi hiperboli \(h\) z ogniskami \(P_1\) i \(P_2\) (gdzie różnica w odległościach Adama od \(P_1\) i \(P_2\) wynosi zaledwie \(24\,\text{km}\)). Korzystne jest umieszczenie początku układu współrzędnych w środku odcinka \(P_1P_2\), tak aby równanie hiperboli \(h\) miało najprostszą możliwą postać.
Oznaczmy początek układu \(O\) i umieśćmy go w środku odcinka \(P_1P_2\). Dodatni kierunek osi \(x\) będzie wyznaczony przez półprostą \(OP_1\), a dodatni kierunek osi \(y\) wybierzemy tak, aby druga współrzędna punktu \(P_3\) była dodatnia. Ponieważ wszystkie podane wymiary są wielokrotnościami \(12\), wybieramy jednostki na obu osiach, aby odpowiadały odległości \(12\,\text{km}\). Sytuację ilustruje rysunek:
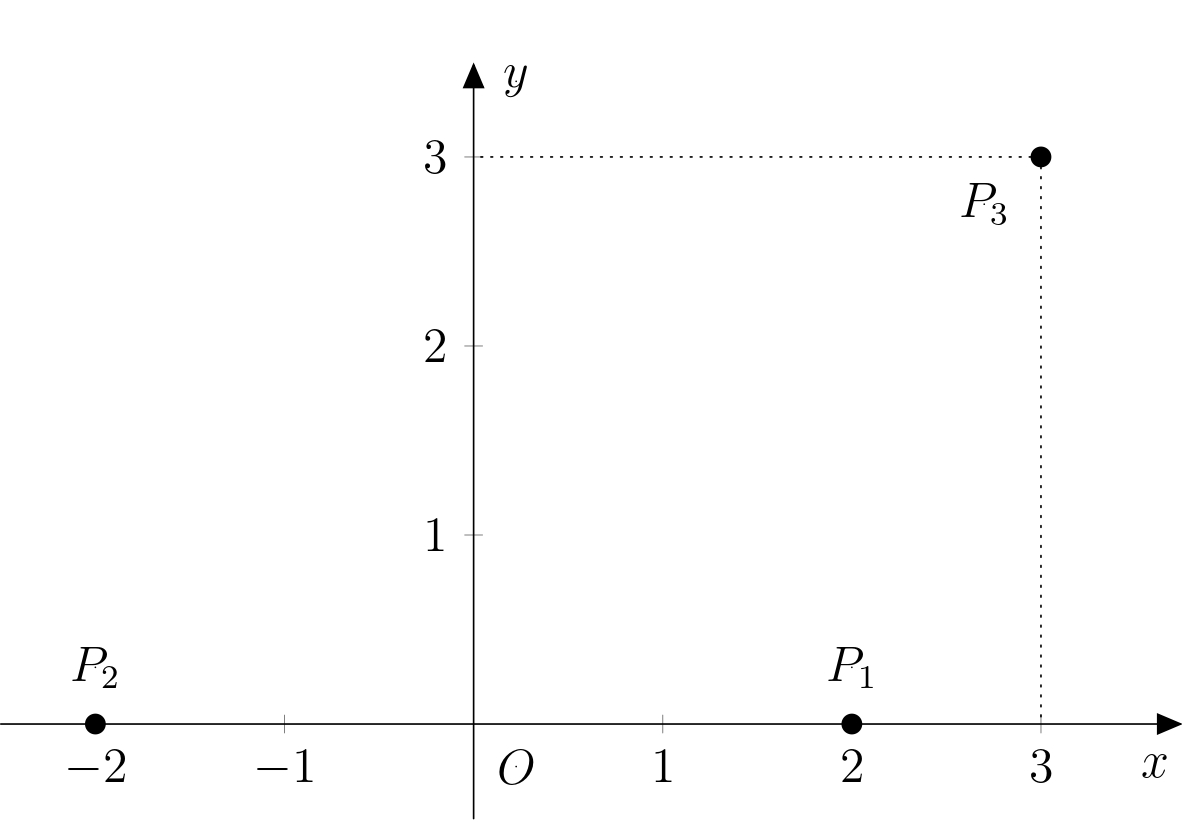
Niech \(A\) oznacza nieznane położenie Adama. Wiemy, że punkt \(A\) leży na osi odcinka \(P_1P_3\). Wyrażamy tę oś (oznaczmy ją \(o\)) parametrycznie: \[o\colon X = S_{P_1P_3}+t\cdot \overrightarrow{u_o},\] gdzie \(S_{P_1P_3}\left[\frac{5}{2};\frac{3}{2}\right]\) i \(\overrightarrow{u_o}=(3;-1)\).Wtedy
\[ \begin{aligned} x &= \tfrac{5}{2} + 3t\\ y &= \tfrac{3}{2} - t,\quad t\in\mathbb{R}. \end{aligned} \]
Aby znaleźć równanie hiperboli, należy zauważyć, że punkty \(P_1\) i \(P_2\) są ogniskami hiperboli \(h\) o środku \(O\) i mimośrodzie \(e\) równym połowie \(|OP_1|\), a więc \(e=2\). Następnie, ponieważ różnica \(|AP_1|-|AP_2|=2\) jest dwa razy większa od długości głównej półosi hiperboli, długość głównej półosi \(a\) jest równa \(1\). Obliczamy długość mniejszej półosi \(b\) poprzez podstawienie do zależności \(b=\sqrt{e^2-a^2}=\sqrt{4-1}=\sqrt{3}\). Teraz możemy zapisać równanie wymaganej hiperboli \[h\colon x^2-\frac{y^2}{3}=1.\] Punkt \(A\) leży na jego prawej gałęzi (jest bliżej odbiornika \(P_1\)), tzn. jego pierwsza współrzędna musi koniecznie wynosić \(x_A>0\).
Obliczmy teraz współrzędne punktów przecięcia linii \(o\) i hiperboli \(h\). Podstawiając równania parametryczne prostej \(o\) do równania hiperboli, otrzymujemy: \[ \begin{aligned} \left(\frac{5}{2} + 3t\right)^2-\frac{\left(\frac{3}{2}-t\right)^2}{3} &= 1 \\ 3\cdot \left(\frac{5}{2} + 3t \right)^2-\left(\frac{3}{2}-t\right)^2 &= 3 \\ \vdots & \\ 52 t^2 +96t +27 &= 0 \end{aligned} \] Pierwiastkami tego równania kwadratowego są \(t_1=-\frac{9}{26}\) i \(t_2=-\frac{3}{2}\). Podstawiamy \(t_1\) do równań parametrycznych i otrzymujemy: \[ \begin{aligned} x_1 &= \tfrac{5}{2} + 3\cdot \left(-\tfrac{9}{26}\right) = \tfrac{19}{13}\\ y_1 &= \tfrac{3}{2} - \left(-\tfrac{9}{26}\right) = \tfrac{24}{13}, \end{aligned} \] czyli \(A_1\left[ \tfrac{19}{13};\tfrac{24}{13} \right]\).Analogicznie, podstawiając \(t_2\), otrzymujemy: \[ \begin{aligned} x_2 &= \tfrac{5}{2} + 3\cdot \left(-\tfrac{3}{2}\right) = -2\\ y_2 &= \tfrac{3}{2} - \left(-\tfrac{3}{2}\right) = 3, \end{aligned} \] i.e., \(A_2 \left[ -2;3 \right]\). Jednak punkt \(A_2\) nie spełnia warunku \(x_A > 0\) (leży na drugiej gałęzi hiperboli), otrzymujemy więc jedyną możliwą pozycję Adama, mianowicie \(A\left[ \tfrac{19}{13};\tfrac{24}{13} \right]\). Rozwiązanie pokazano na rysunku.
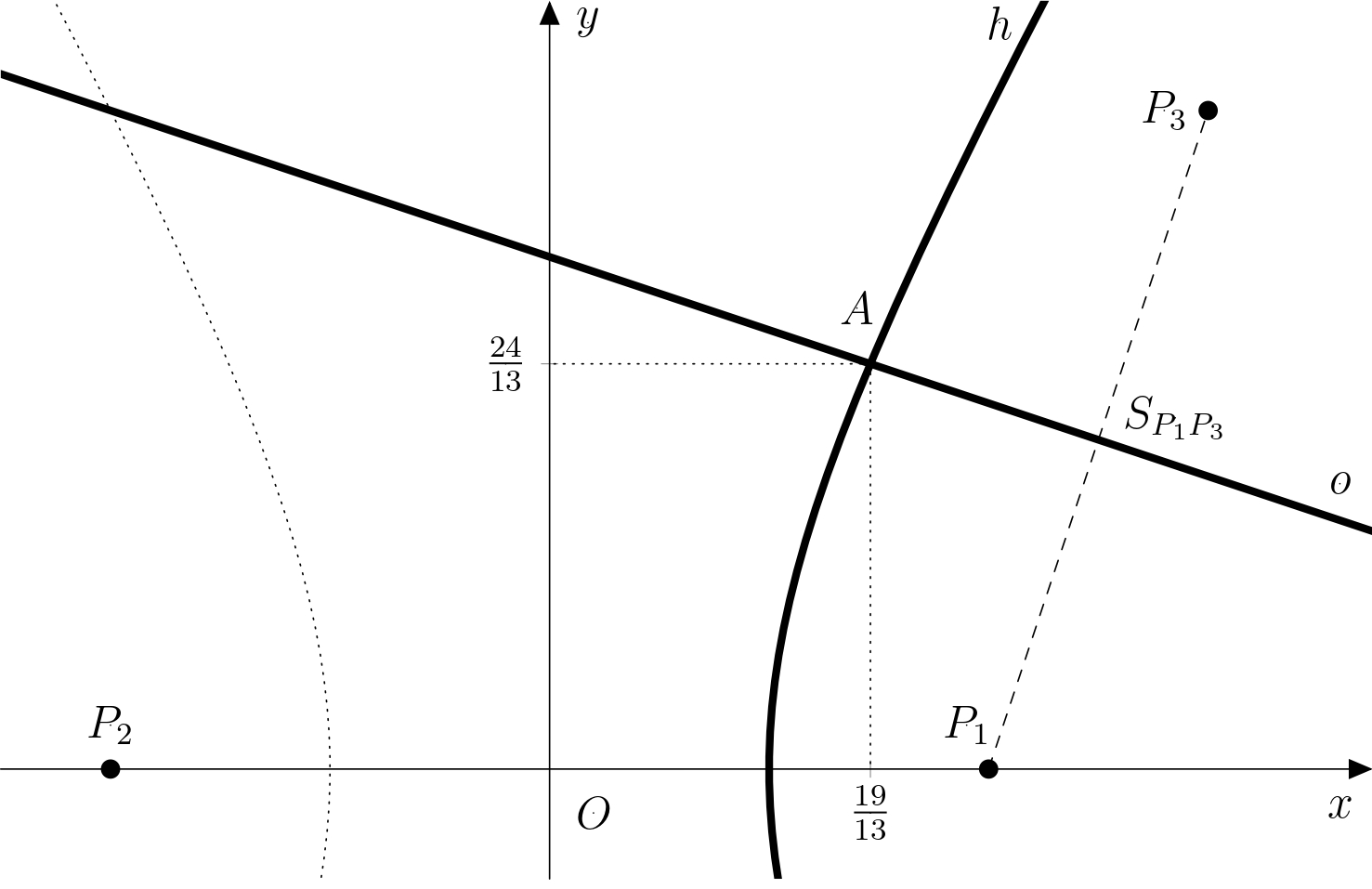
Uwaga Gdyby Adam nie był w równej odległości od odbiorników \(P_1\) i \(P_3\), rozwiązanie zadaniu oznaczałoby znalezienie przecięcia gałęzi dwóch hiperbol. Takie obliczenia wykraczałyby jednak poza zakres matematyki w szkole średniej. ## Literatura