Tieň domu
 40 min.,
40 min.,  3/3
3/3 Martin si chce na svojom plátne rozvrnúť miesto na nakreslenie domu za slnečného dňa. Znázornil si preto jednoduchý model domu v rovnobežnom premietaní, ktorý stojí na vodorovnom pozemku. Dom je tvorený obdĺžnikovým kvádrom s jednoduchou valbovou strechou. Valbová strecha je strecha tvorená dvoma rovnoramennými trojuholníkmi a dvoma rovnoramennými lichobežníkmi. Všetky štyri roviny strechy majú rovnaký sklon. Na plátno vedľa domu umiestnil zvislú tyč a jej tieň (pozri obrázok).
Na popis riešenia budeme potrebovať nasledujúce pojmy:
- Vlastný tieň na objekte je tá časť povrchu objektu, ktorá nie je osvetlená svetelným zdrojom. Čiara na povrchu objektu, ktorá oddeľuje osvetlené a neosvetlené časti sa nazýva hranica vlastného tieňa.
- Vrhnutý tieň je tieň, ktorý objekt vrhá na nejakú plochu v dôsledku osvetlenia. Hranica vrhnutého tieňa je obrys tohto tieňa na ploche.
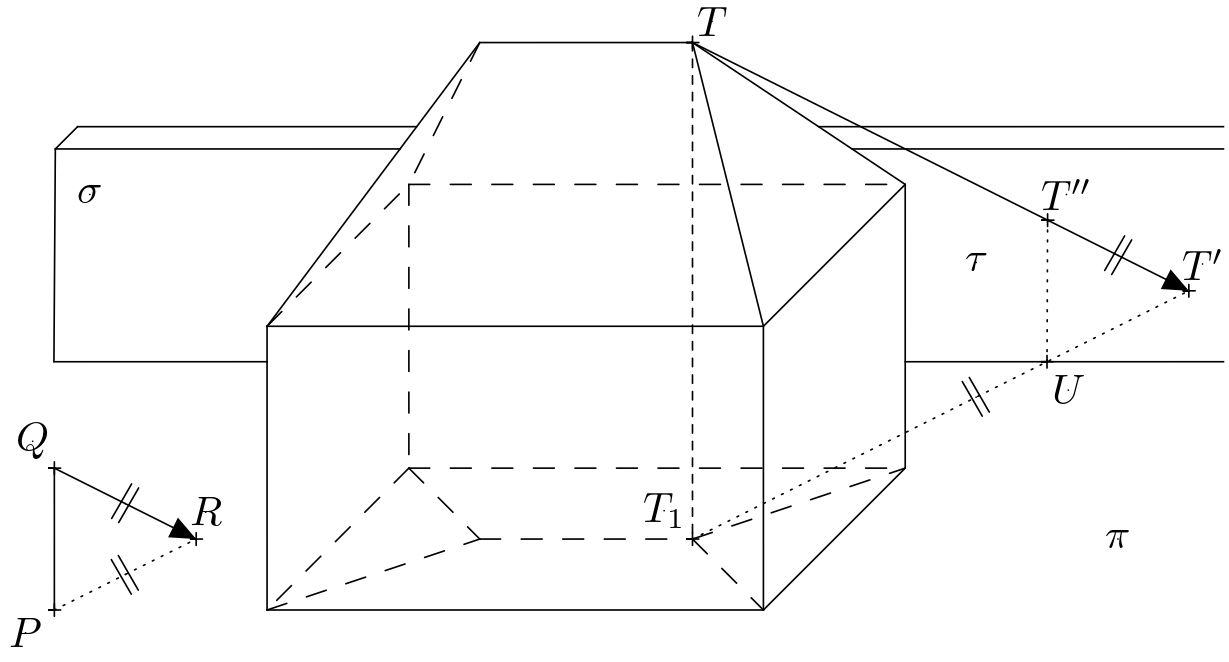
Úloha 1. Vyznačte na obrázku vlastný tieň domu a tieň domu vrhnutý na zem slnkom. (Vzdialenosť Slnka od povrchu Zeme je taká veľká, že môžeme považovať slnečné lúče za navzájom rovnobežné.) 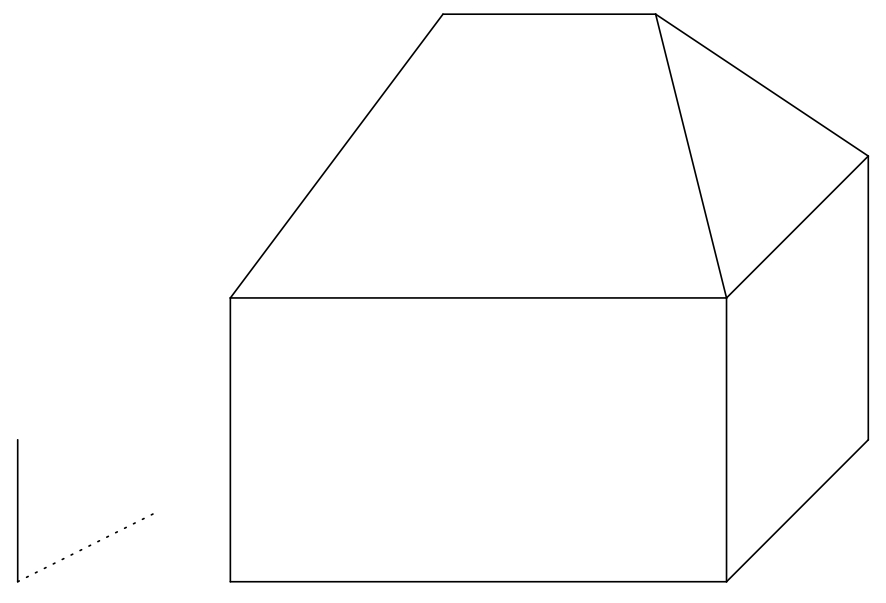
Riešenie. Nech \(P\) označuje pätu tyče, \(Q\) jej horný koniec a \(R\) vrhnutý tieň bodu \(Q\). Orientovaná úsečka \(QR\) teda určuje smer a orientáciu svetelných lúčov. Úsečka \(PR\) je kolmý priemet úsečky \(QR\) do roviny zeme. V nasledujúcom texte označíme rovinu zeme symbolom \(\pi\). Ďalej označíme vrcholy kvádra \(ABCDEFGH\) a označíme koncové body hrebeňa strechy symbolmi \(S\) a \(T\).
Osvetlenou časťou domu je ľavá bočná a predná stena kvádra a zodpovedajúce časti strechy. Hranicou vlastného tieňa je teda uzavretá lomená čiara \(ABFTSHDA\). Na určenie hranice vrhnutého tieňa domu stačí zostrojiť vrhnuté tiene vrcholov tejto lomenej čiary. Z nich \(A\), \(B\) a \(D\) už ležia v rovine \(\pi\), a preto sú aj ich vlastnými vrhnutými tieňmi. Preto stačí zostrojiť vrhnuté tiene bodov \(F\), \(T\), \(S\) a \(H\).
Vrhnutý tieň bodu \(T\) je priesečníkom svetelného lúča prechádzajúceho týmto bodom s kolmým priemetom tohto lúča do roviny \(\pi\). Pripomeňme, že smer svetelných lúčov je určený priamkou \(QR\) a smer kolmého priemetu lúčov do roviny \(\pi\) je určený priamkou \(PR\). Kolmý priemet lúča ďalej prechádza bodom \(T_1\), ktorý je kolmým priemetom bodu \(T\) do roviny \(\pi\). Ak označíme vrhnutý tieň bodu \(T\) ako \(T'\), tak jeho konštrukcia je znázornená na obrázku.
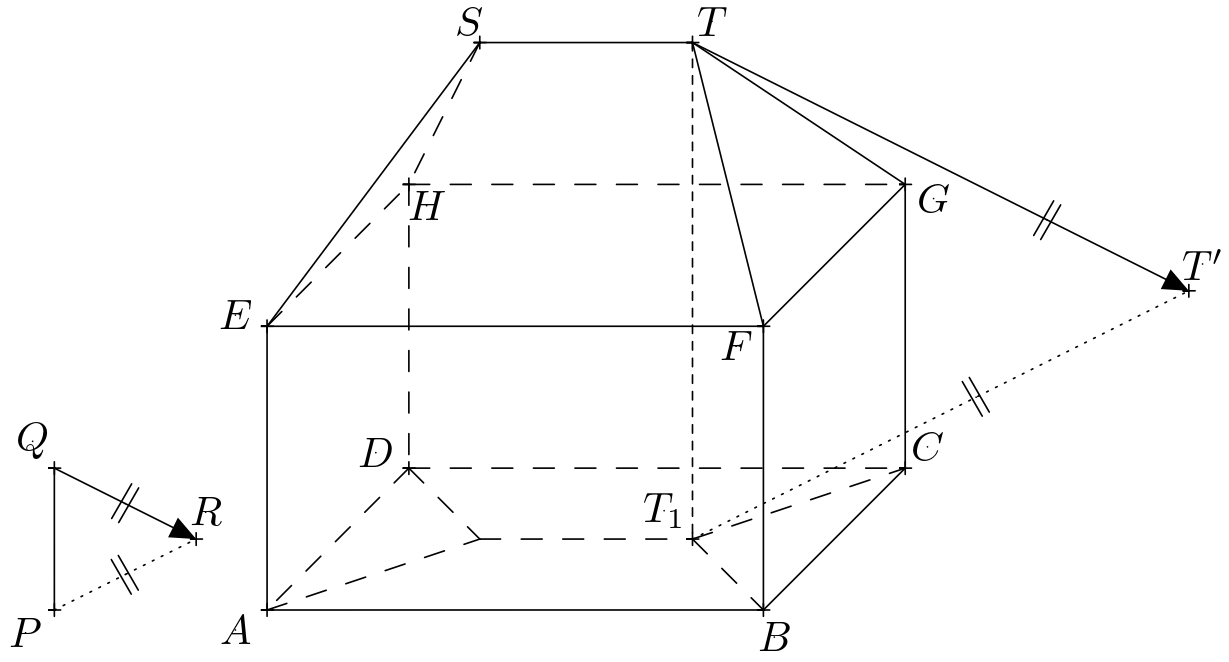
Podobne zostrojíme vrhnuté tiene \(F'\), \(S'\), \(H'\) bodov \(F\), \(S\) a \(H\). Hranicou vrhnutého tieňa domu je potom mnohouholník \(ABF'T'S'H'D\). Pri tieňovaní zohľadňujeme iba viditeľné časti vlastného a vrhnutého tieňa.
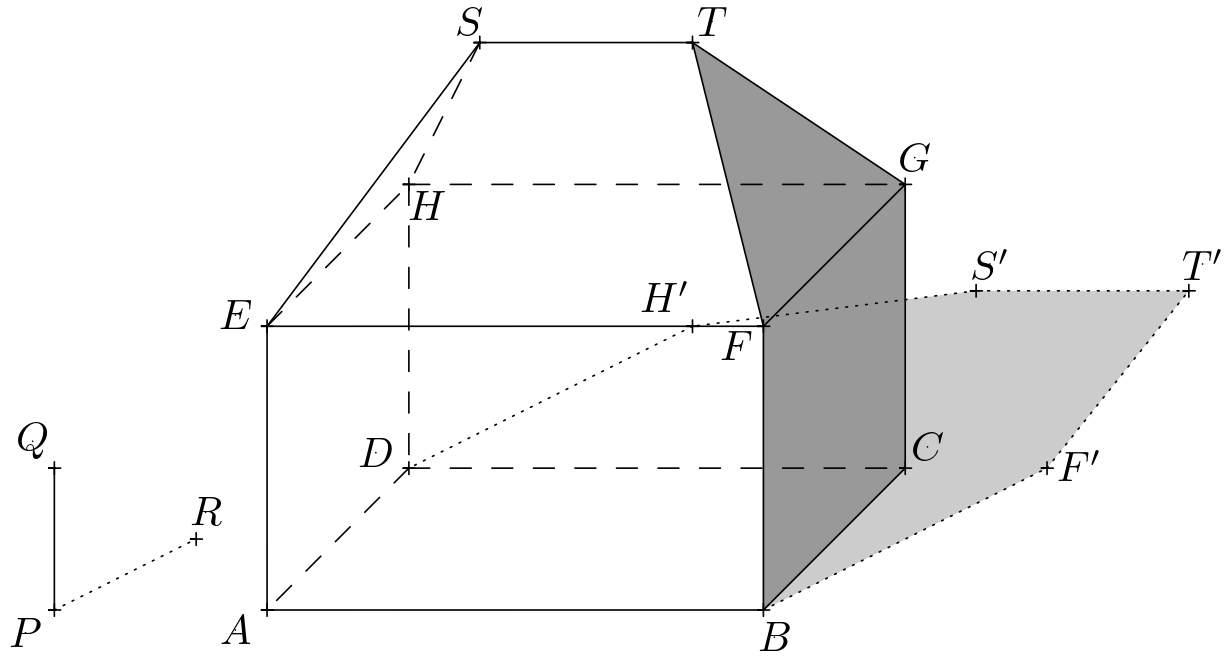
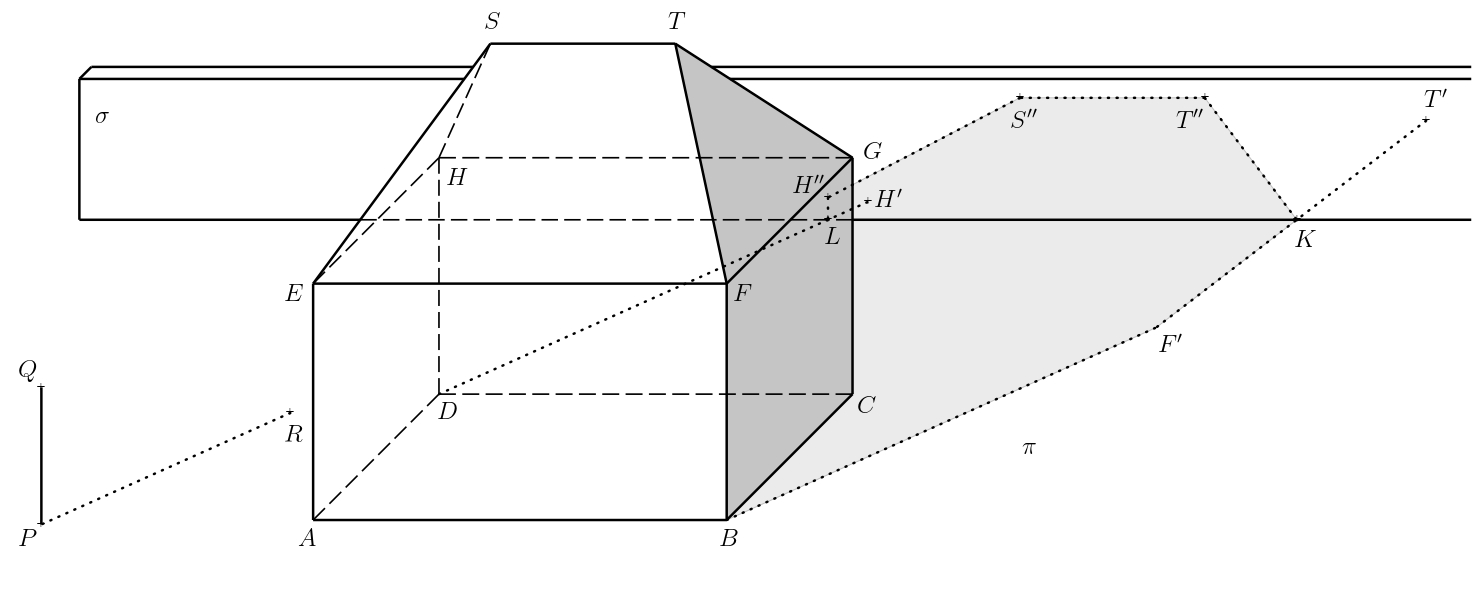
Úloha 2. Narysujte vrhnutý tieň domu, ak je za domom nepriehľadná stena, ktorá je rovnobežná s prednou a zadnou stenou domu 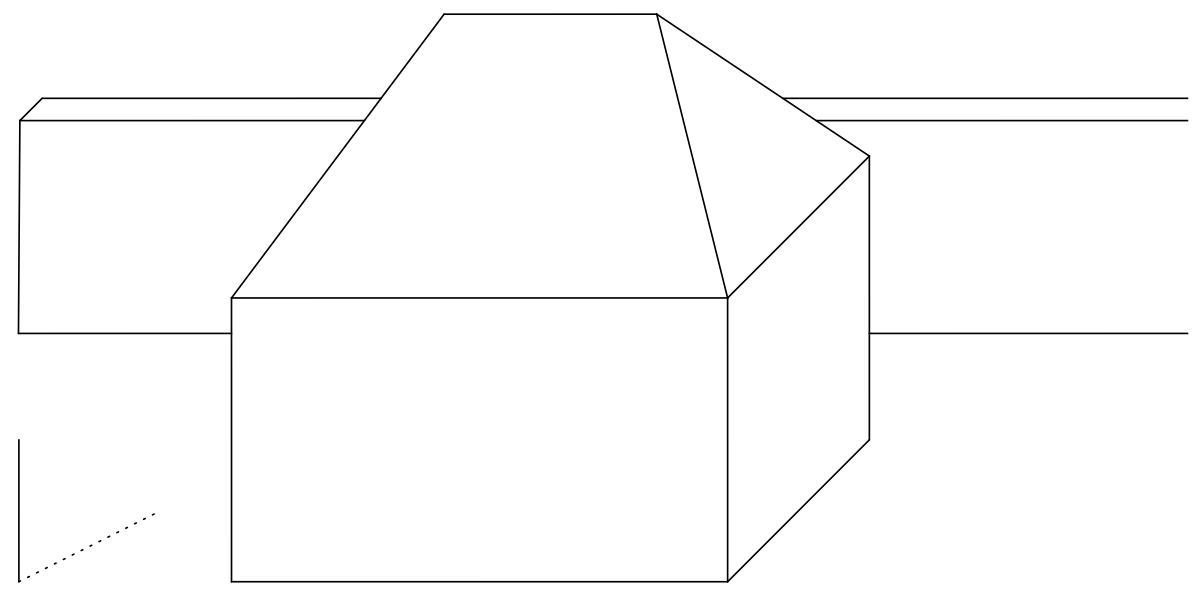
Riešenie. Vlastný tieň domu, jeho hranica a vrhnuté tiene bodov do roviny \(\pi\), ktoré sú z nášho pohľadu umiestnené pred stenou, zostávajú nezmenené. Označme symbolom \(\sigma\) rovinu, v ktorej leží predná strana pridanej steny. Pre trojicu bodov \(T\), \(S\) a \(H\) je potrebné zostrojiť ich vrhnuté tiene do tejto roviny. Konštrukciu opíšeme opäť len pre bod \(T\).
Zvážte body \(T_1\) a \(T'\) z predchádzajúcej úlohy. Nech \(\tau\) označuje rovinu \(TT_1T'\), a ďalej označme bodom \(U\) priesečník priamky \(T_1T'\) a dolnej hrany steny (t. j. \(\sigma \cap \pi\)).
Týmto bodom musí prechádzať aj priesečnica rovín \(\sigma\) a \(\tau\), t. j. tieňom \(T_1T\) vrhnutým do roviny \(\sigma\). Táto priesečnica musí byť navyše zvislá, pretože obe roviny \(\tau\) a \(\sigma\) sú zvislé. Vrhnutý tieň bodu \(T\) do roviny \(\sigma\) (označme ho \(T''\)) potom leží na uvedenej priesečnici a priamke \(TT'\).
Podobne zostrojíme vrhnuté tiene \(S''\) a \(H''\) bodov \(S\) a \(H\). Hranicou vlastného tieňa je potom uzavretá lomená čiara \(ABF'KT''S''H''LDA\), kde bod \(K\) (resp. \(L\)) leží na priesečnici rovín \(\sigma\) a \(\pi\) a zároveň na úsečke \(F'T'\) (resp. \(DH'\)). Tieňujeme iba viditeľné časti vlastného a vrhnutého tieňa, nebudeme tieňovať časti tieňa zakryté domom.
Poznámka. Pre lepšiu predstavu môže pomôcť aj interaktívny applet v GeoGebre. V applete je možné do určitej miery upraviť smer slnečných lúčov, pozri https://www.geogebra.org/m/ecyqv4qg
Úloha 3. Vyznačte na obrázku vlastný tieň domu a tieň domu vrhnutý na zem slnkom. (Vzdialenosť Slnka od povrchu Zeme je taká veľká, že môžeme považovať slnečné lúče za navzájom rovnobežné.)
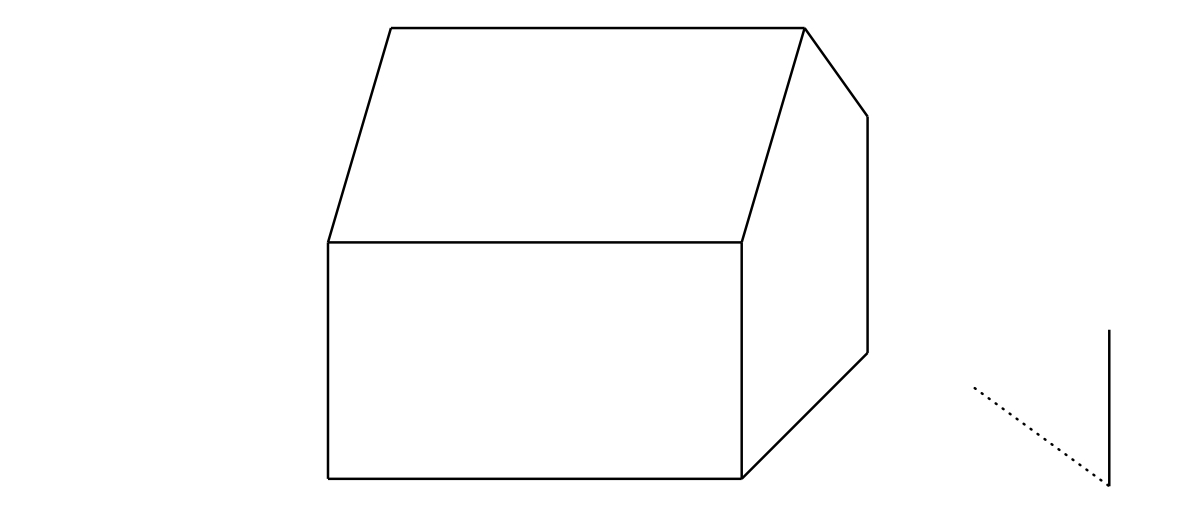
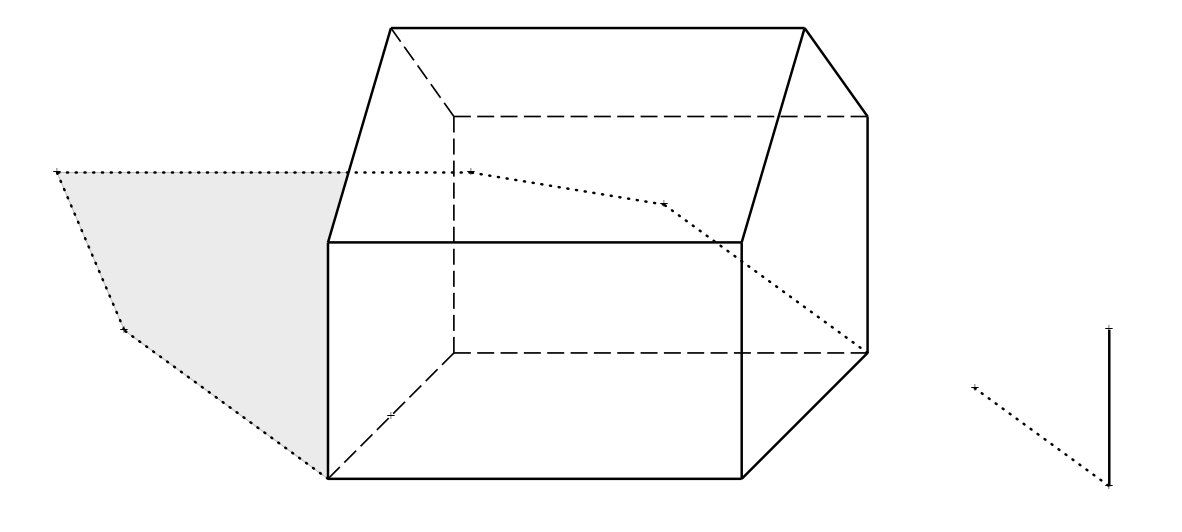
Riešenie.
Literatúra
- Pomykalová E. Deskriptivní geometrie pro střední školy. Prometheus. 2010. 106—107.