Pokroky na poli elektrotechniky umožnily vývoj nových navigačních systémů založených na přenosu elektromagnetického vlnění. Příkladem takového systému je námořní navigace LORAN-C, která byla vyvinuta za druhé světové války v USA. U tohoto typu navigace plavidlo přijímá synchronizovaný signál z dvojice vysílačů. Signál ze vzdálenějšího vysílače je plavidlem přijat později, zpoždění signálu tedy určuje rozdíl mezi vzdálenostmi plavidla od prvního a druhého vysílače.
Množina bodů, které mají stálý rozdíl vzdáleností od dvou daných pevných bodů, je hyperbola. Víme tedy, že plavidlo se nachází na hyperbole, jejíž ohniska jsou právě vysílače, a která je určena rozdílem vzdáleností plavidla od těchto vysílačů. Zpoždění signálu z jiné dvojice stanic pak určuje druhou hyperbolu, na které plavidlo musí ležet. Leží-li plavidlo na jedné i druhé hyperbole, leží v jejich průsečíku.
Úloha 1. V krajině jsou rozmístěny tři přijímače \(P_1\), \(P_2\) a \(P_3\). Známé vzdálenosti zachycuje obrázek:
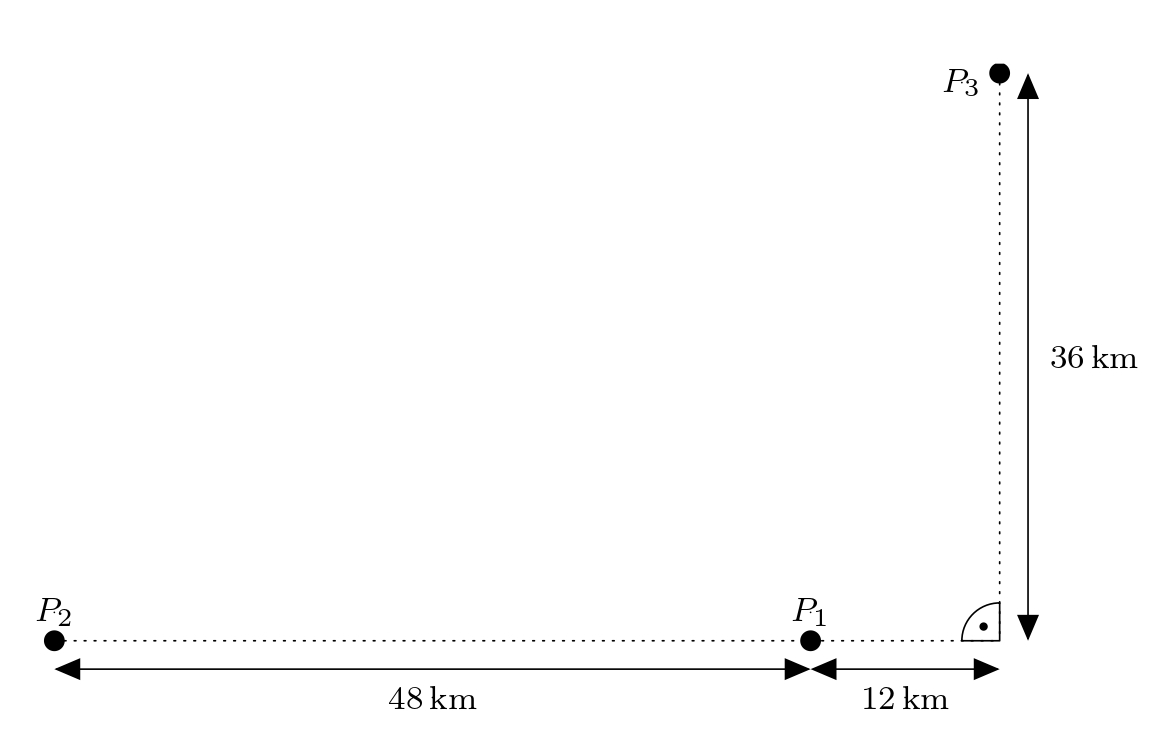
Adamova turistická navigace vyšle signál ke všem třem přijímačům. Signál dorazí k přijímačům \(P_1\) a \(P_3\) ve stejnou dobu a k přijímači \(P_2\) o 80 mikrosekund později. Určete, kde se Adam nachází. Předpokládejte, že signál urazí 300 000 km za sekundu. Polohu určete ve vhodně zavedené soustavě souřadnic.
Řešení. Nejprve v obrázku vhodně zvolíme kartézskou soustavu souřadnic. Volbu zdůvodníme takto: protože je Adam stejně vzdálen od přijímače \(P_1\) i \(P_3\), nachází se jeho poloha na ose úsečky \(P_1P_3\). Skutečnost, že k přijímači \(P_2\) dorazí jeho signál o 80 mikrosekund později než k přijímači \(P_1\) znamená, že je od přijímače \(P_2\) o \(24\,\text{km}\) dále než od přijímače \(P_1\). Jeho poloha se proto také nachází na větvi hyperboly \(h\) s ohnisky \(P_1\) a \(P_2\) (kde rozdíl vzdáleností Adama od \(P_1\) a \(P_2\) je roven právě \(24\,\text{km}\)). Aby měla hyperbola \(h\) co nejjednodušší rovnici je výhodné umístit počátek soustavy souřadnic do středu úsečky \(P_1P_2\).
Označme tedy počátek soustavy \(O\) a položme jej do středu úsečky \(P_1P_2\). Kladný směr osy \(x\) bude určovat polopřímka \(OP_1\) a kladný směr osy \(y\) zvolíme tak, aby byla druhá souřadnice bodu \(P_3\) kladná. Protože všechny zadané rozměry jsou násobky \(12\), jednotky na obou osách zvolíme tak, aby odpovídaly vzdálenosti \(12\,\text{km}\). Situaci znázorňuje obrázek:
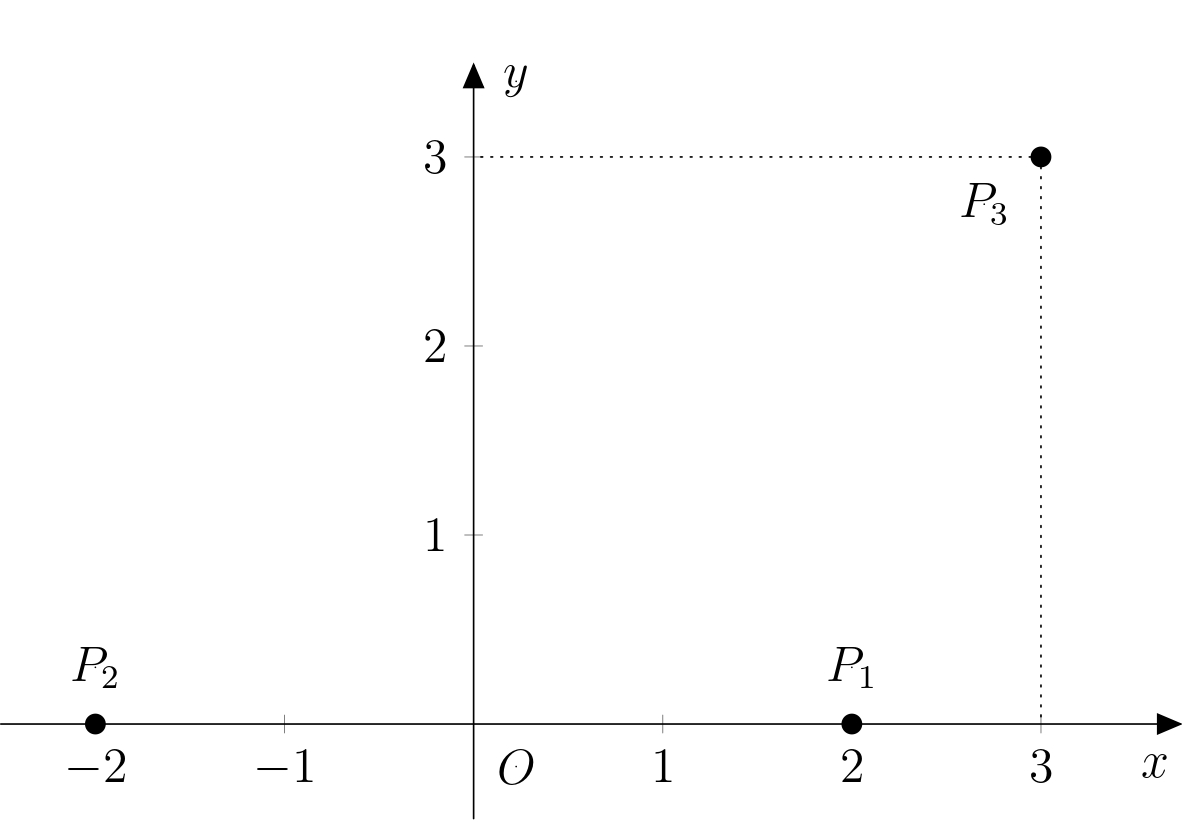
Označme neznámou polohu Adama \(A\). Víme, že bod \(A\) leží na ose úsečky \(P_1P_3\), proto si tuto osu (označme ji \(o\)) vyjádříme parametricky: \[o\colon X = S_{P_1P_3}+t\cdot \overrightarrow{u_o},\] kde \(S_{P_1P_3}\left[\frac{5}{2};\frac{3}{2}\right]\) a \(\overrightarrow{u_o}=(3;-1)\). Pak
\[ \begin{aligned} x &= \tfrac{5}{2} + 3t\\ y &= \tfrac{3}{2} - t,\quad t\in\mathbb{R}. \end{aligned} \]
Určeme nyní rovnici hyperboly. Jelikož jsou body \(P_1\) a \(P_2\) ohniska hyperboly \(h\), je středem hyperboly bod \(O\) a její excentricita \(e\) je rovna polovině \(|OP_1|\), tedy \(e=2\). Dále, protože je rozdíl \(|AP_1|-|AP_2|=2\) dvojnásobkem délky hlavní poloosy hyperboly, je délka hlavní poloosy \(a\) rovna \(1\). Délku vedlejší poloosy \(b\) vypočítáme dosazením do vztahu \(b=\sqrt{e^2-a^2}=\sqrt{4-1}=\sqrt{3}\). Můžeme tak napsat rovnici hledané hyperboly \[h\colon x^2-\frac{y^2}{3}=1.\] Bod \(A\) leží na její pravé větvi (je blíže přijímači \(P_1\)), tj. nutně musí být jeho první souřadnice \(x_A>0\).
Vypočítejme nyní souřadnice průsečíků přímky \(o\) a hyperboly \(h\). Dosazením parametrických rovnic přímky do rovnice hyperboly tak dostáváme \[ \begin{aligned} \left(\frac{5}{2} + 3t\right)^2-\frac{\left(\frac{3}{2}-t\right)^2}{3} &= 1 \\ 3\cdot \left(\frac{5}{2} + 3t \right)^2-\left(\frac{3}{2}-t\right)^2 &= 3 \\ \vdots & \\ 52 t^2 +96t +27 &= 0 \end{aligned} \] Kořeny této kvadratické rovnice jsou \(t_1=-\frac{9}{26}\) a \(t_2=-\frac{3}{2}\). Dosadíme \(t_1\) do parametrických rovnic a dostaneme
\[ \begin{aligned} x_1 &= \tfrac{5}{2} + 3\cdot \left(-\tfrac{9}{26}\right) = \tfrac{19}{13}\\ y_1 &= \tfrac{3}{2} - \left(-\tfrac{9}{26}\right) = \tfrac{24}{13}, \end{aligned} \] tj. \(A_1\left[ \tfrac{19}{13};\tfrac{24}{13} \right]\). Podobně dosazením \(t_2\) dostaneme \[ \begin{aligned} x_2 &= \tfrac{5}{2} + 3\cdot \left(-\tfrac{3}{2}\right) = -2\\ y_2 &= \tfrac{3}{2} - \left(-\tfrac{3}{2}\right) = 3, \end{aligned} \] tj. \(A_2 \left[ -2;3 \right]\). Bod \(A_2\) však nevyhovuje podmínce \(x_A > 0\) (leží na druhé větvi hyperboly), tedy dostáváme jedinou možnou Adamovu polohu, a to \(A\left[ \tfrac{19}{13};\tfrac{24}{13} \right]\). Řešení je znázorněno na obrázku.
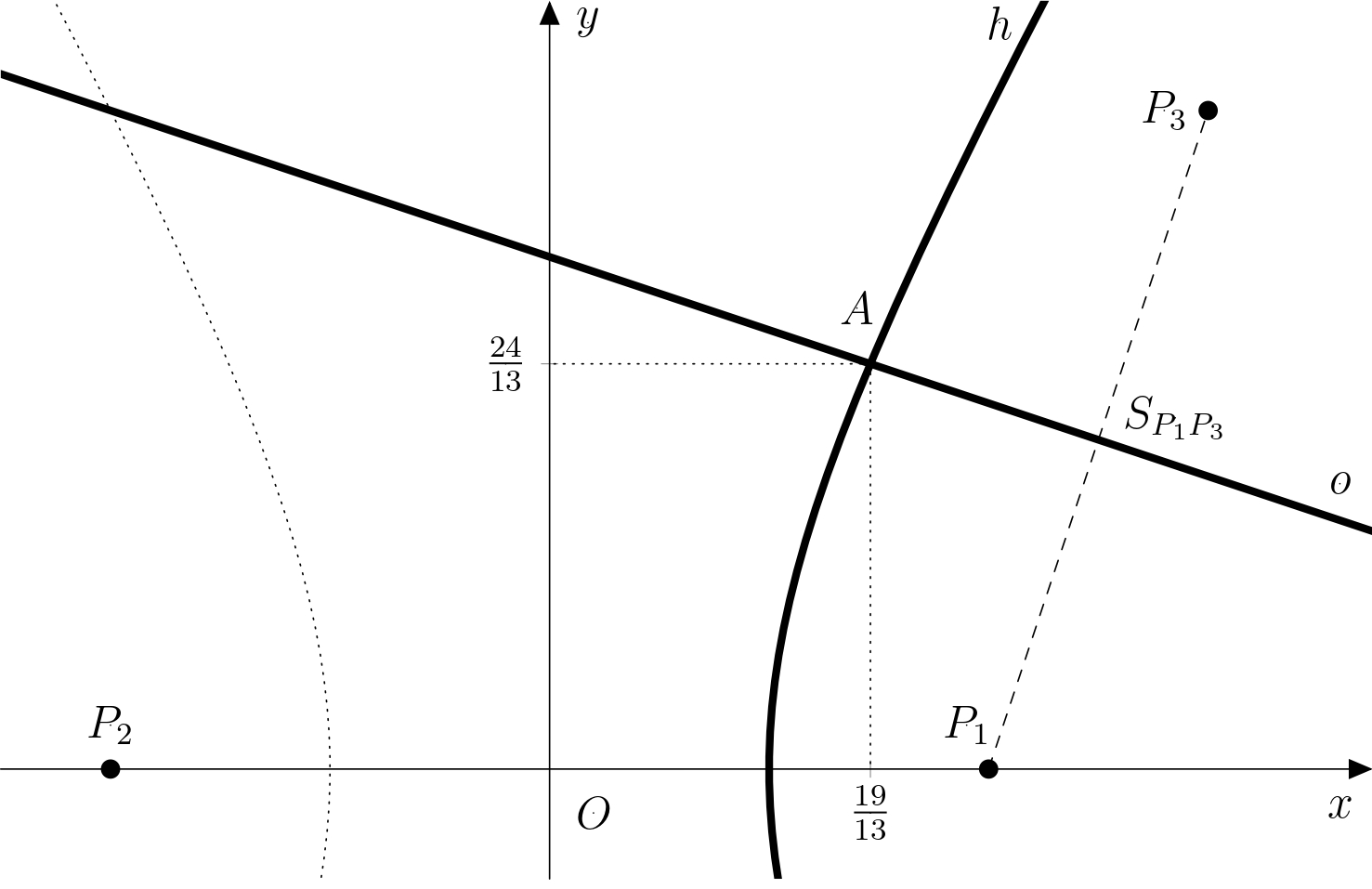
Poznámka. Jestliže by Adam nebyl stejně vzdálený od přijímačů \(P_1\) a \(P_3\), řešit úlohu by znamenalo hledat průsečíky větví dvou hyperbol. Takový výpočet by však byl nad rámec středoškolské matematiky.