Mnoho počítačových i mobilních her je založených na bázi hádanek, ve kterých je k dosažení cíle třeba provést určitou kombinaci tahů, například pomačkat některé z nabízených spínačů, aby fungoval jimi řízený stroj. Takové spínače mají navíc konečný počet stavů, v nichž se mohou nacházet: jsou buď zapnuté, nebo vypnuté. Uveďme si to na příkladu žárovky. Ta buď svítí, nebo nesvítí, a její spínač tak provádí pouze dvě akce. Když je žárovka vypnutá, prvním zmáčknutím spínače ji zapneme a druhým opět vypneme. V informatice je takových systémů, které mají omezený počet stavů, mnoho, a konkrétně hry, v nichž je potřeba uvedeným způsobem navolit optimální kombinaci tahů, díky níž dostaneme správný výsledek, se nazývají konečné lineární hry.
Představme si síť tří žárovek, které jsou pro začátek všechny vypnuté a pod každou z nich je spínací tlačítko. Každé z tlačítek změní stav (zapne nebo vypne) žárovky nad sebou a současně žárovek s ní přímo sousedících. Pojmenujeme-li žárovky a k nim příslušná tlačítka A, B, C, potom stisknutím tlačítka A se rozsvítí žárovka A, ale protože je na kraji, společně s ní se rozsvítí už jen žárovka B. Totéž platí pro žárovku C, také má souseda jen po jedné straně, takže stisknutím tlačítka C se rozsvítí žárovky C a B. Pouze žárovka B sousedí s A i C, proto tlačítko B mění stav všech tří žárovek.
Na následujících třech obrázcích můžeme sledovat, jak by se žárovky postupně rozsvěcovaly a zhasínaly při postupném stisknutí tlačítek A a B. Důležité je si uvědomovat, že nezáleží na pořadí, v němž jsou tlačítka zmáčknuta. Můžeme si představit, že kdybychom nejprve stiskli B, rozsvítí se všechny žárovky, a následný stisk A zhasne žárovky A a B, takže zůstane svítit pouze C.
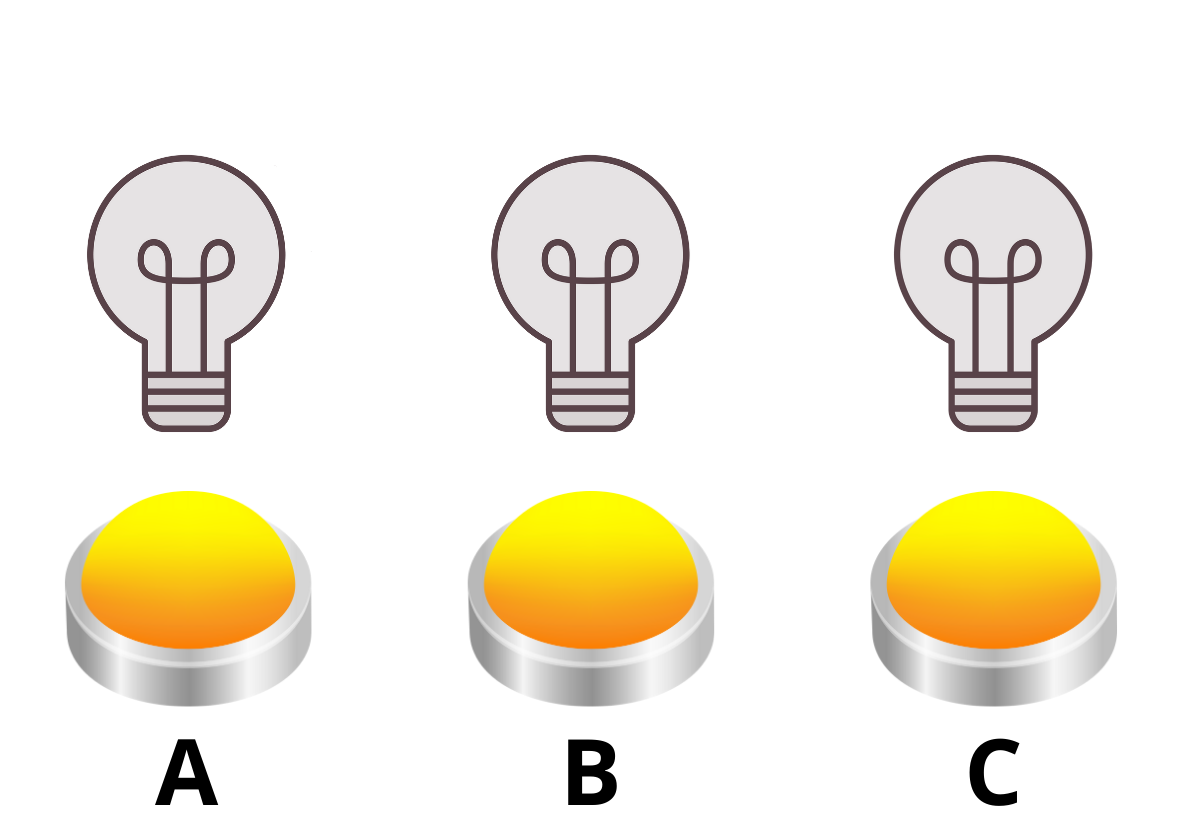
Pro následující úlohy je stěžejní pojem konečného počtu. V případě žárovek, které vždy buď svítí, nebo nesvítí, můžeme identifikovat několik situací, které se buď dějí („ano“), nebo nedějí („ne“), a protože jsme v matematice, místo slov můžeme používat značení dvojkové soustavy: ano = 1, ne = 0, tj.
V tomto označení navíc platí \(1+1=0\) nebo také \(2k=0\), \(k\in\mathbb{Z}\), a současně \(1=-1\). V případě žárovek se to projevuje tak, že když dvakrát zmáčkneme stejné tlačítko, příslušnou žárovku to rozsvítí a zase zhasne (nebo naopak), takže se dostane do původního stavu a vychází to nastejno, jako kdybychom toto tlačítko nezmáčkli vůbec.
Vliv jednotlivých tlačítek na všechny žárovky můžeme zapsat vektorově. Vektory \(\textbf{a}\), \(\textbf{b}\), \(\textbf{c}\) budou popisovat činnost tlačítek A, B, C. Každá souřadnice vektoru popisuje příslušnou žárovku v pořadí: první A, druhá B, třetí C. Označení 1 znamená, že tlačítko mění stav dané žárovky, a 0, že na ni nemá vliv. Podle uvedených vlastností tlačítek platí
\[ \textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}. \]
Pomocí vektorů lze popsat i konkrétní stavy žárovek. Žárovka svítí: 1, nebo nesvítí: 0. Počáteční stav, kdy nesvítí žádná žárovka, by popsal vektor \[ \textbf{s}=\begin{bmatrix} 0\\0\\0\end{bmatrix}. \] Následným stisknutím tlačítek A a B jsme se dostali ke třetímu obrázku. Vektorově zapsáno za využití sčítání v soustavě popisující stav žárovek platí
\[ \textbf{s}+\textbf{a}+\textbf{b}= \begin{bmatrix}0\\0\\0\end{bmatrix}+ \begin{bmatrix}1\\1\\0\end{bmatrix}+ \begin{bmatrix}1\\1\\1\end{bmatrix}= \begin{bmatrix} 0+1+1 \\ 0+1+1 \\ 0+0+1 \end{bmatrix}= \begin{bmatrix}0\\0\\1\end{bmatrix}. \]
Úloha 1. Určete kombinaci tlačítek, které je potřeba stisknout, aby svítily pouze žárovky A a C, pokud jsou na počátku všechny tři žárovky zhasnuté.
Řešení. Hledaný výsledný stav lze popsat vektorem \[ \textbf{t}=\begin{bmatrix}1\\0\\1\end{bmatrix}. \] Úlohu vyřešíme jako soustavu lineárních rovnic \[\textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t}, \] kde vektory \({\textbf{a}}\), \({\textbf{b}}\), \({\textbf{c}}\) popisují, které žárovky jsou daným tlačítkem ovládány, jak bylo uvedeno výše, a proměnné \(x_1, x_2, x_3\) nabývají hodnot 1 nebo 0 podle toho, zda příslušné tlačítko využijeme, či nikoliv.
Napoprvé soustavu uvedeme i s nulovými koeficienty, aby bylo jasně vidět, jak jsou do soustavy přepsány souřadnice vektorů \({\textbf{a}}\), \({\textbf{b}}\), \({\textbf{c}}\).
\[ \begin{aligned} 0 + 1x_1 + 1x_2 + 0x_3 &= 1\\ 0 + 1x_1 + 1x_2 + 1x_3 &= 0\\ 0 + 0x_1 + 1x_2 + 1x_3 &= 1 \end{aligned} \]
Soustavu řešíme například dosazovací metodou:
\[ \begin{alignedat}{3} x_1 &+ x_2& && &= 1 \Rightarrow x_1 = 1-x_2\\ x_1 &+ x_2& &+ x_3&&= 0\\ && x_2 &+ x_3&&= 1 \Rightarrow x_3 = 1-x_2 \end{alignedat} \]
Dosadíme do druhé rovnice:
\[ \begin{aligned} (1-x_2) + x_2 + (1-x_2) &= 0\\ 2 - x_2 &= 0\\ x_2 &= 2, \end{aligned} \]
ale protože pracujeme v naší soustavě máme \(2=0\), platí \(x_2 = 0\). Dosazením dostáváme \(x_1=1, x_3=1\), což znamená, že máme zmáčknout tlačítka A a C, abychom docílili toho, že budou svítit žárovky A a C a žárovka B bude zhasnutá.
Poznámka. Úlohy pro tři žárovky lze velice snadno vyřešit z hlavy, jelikož každé tlačítko mačkáme nanejvýš jednou. Víckrát to ani nemá smysl, když dvě zmáčknutí stejného tlačítka vycházejí stejně jako žádné zmáčknutí. V následující úloze proto zvětšíme počet žárovek, to však povede na soustavu více než tří lineárních rovnic o více než třech neznámých, které už se v běžné výuce matematiky pravděpodobně nepočítají. Úlohy proto mohou posloužit do speciálního semináře, ve kterém jsou žáci seznámeni s maticovým počtem a mohou ho tím procvičit na konkrétní slovní úloze.
Úloha 2. Síť žárovek rozšíříme na pět kusů a tlačítka mají stále stejnou vlastnost, že ovládají žárovku nad sebou a její přímé sousedy. Na počátku nejsou všechny žárovky zhasnuty, ale už svítí žárovky A a D.
Zjistěte, jakou kombinaci tlačítek zmáčknout, aby na konci - byly všechny žárovky zhasnuté, - svítila pouze žárovka E.
Řešení. Kromě počtu lineárních rovnic a proměnných v soustavě se řešení bude lišit také pozměněným počátečním stavem, kdy všechny žárovky nejsou ve stavu 0 = zhasnuté. Počáteční stav můžeme zapsat vektorem
\[ \textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix} \] a chování tlačítek A až E popisují vektory \[ \textbf{a}=\begin{bmatrix}1\\1\\0\\0\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\\0\\0\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\\1\\0\end{bmatrix},\quad \textbf{d}=\begin{bmatrix}0\\0\\1\\1\\1\end{bmatrix},\quad \textbf{e}=\begin{bmatrix}0\\0\\0\\1\\1\end{bmatrix}. \]
Pokud chceme, aby všechny žárovky byly zhasnuté, tak řešíme soustavu rovnic
\[ \textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} + x_4\textbf{d} + x_5\textbf{e}= \textbf{t}, \] kde \[ \textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\\0\\0\end{bmatrix}. \]
Vektor \({\textbf{s}}\) převedeme na pravou stranu
\[ x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} + x_4\textbf{d} + x_5\textbf{e}= \textbf{t} - \textbf{s}, \] a zapíšeme soustavu pěti lineárních rovnic o pěti neznámých \[ \begin{alignedat}{8} x_1 &+& &x_2& && && && && && &= 0-1 \\ x_1 &+& &x_2& &+& &x_3& && && && &= 0 \\ && &x_2& &+& &x_3& &+& &x_4& && &=0 \\ && && && &x_3& &+& &x_4& &+& x_5 &=0-1 \\ && && && && && &x_4& &+& x_5 &=0 \end{alignedat} \] Při řešení pamatujeme na to, že v námi uvažované soustavě platí \(-1=1\) a \(2=0\). Soustava má dvě řešení, jimiž jsou uspořádané pětice \((0,1,1,0,0)\) a \((1,0,1,1,1)\).
Má-li na konci svítit pouze žárovka E, platí \[ \textbf{t} = \begin{bmatrix}0\\0\\0\\0\\1\end{bmatrix}. \] Po pár úpravách (sčítací metodou nebo při práci s maticemi Gaussovou eliminační metodou) bychom zjistili, že pro takové zadání soustava nemá řešení. Nelze tedy žárovky z původního stavu, kdy svítí pouze A a D, dostat do stavu, aby svítila samotná žárovka E.
Úloha 3. Nové, modře svítící žárovky se od předchozích liší tím, že mohou svítit ve dvou různých odstínech modré. Pokud je tato žárovka zhasnutá, prvním stisknutím tlačítka, které ji ovládá, se rozsvítí světle modře, druhým stisknutím tmavě modře a po třetím stisknutí opět zhasne. Tlačítka mají stále stejnou vlastnost, tedy ovládají žárovku nad sebou a její přímé sousedy. Kolikrát musíte stisknout které z tlačítek A, B a C, abyste ze stavu na obrázku všechny žárovky zhasli?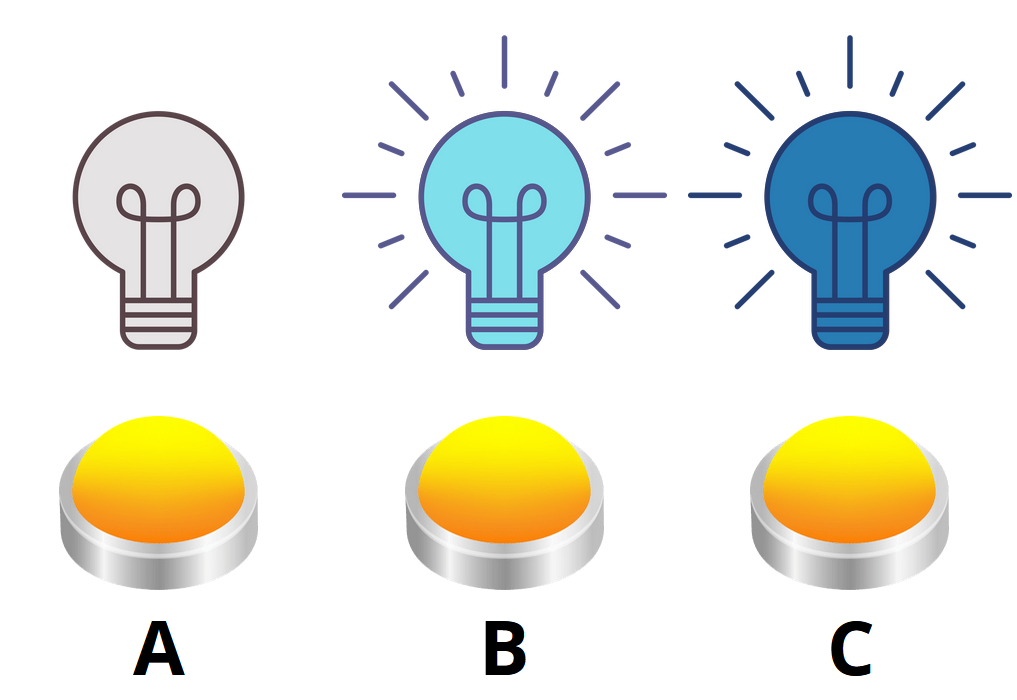 
Řešení. Protože mají žárovky nyní tři stavy, v jakých mohou být, přesouváme se k počítání v trojkové soustavě. Označme žárovka „nesvítí“ = 0, „svítí světle modře“ = 1 a „svítí tmavě modře“ = 2.
Tlačítka A, B, C však danou žárovku mohou pouze ovládat, nebo neovládat, žádná třetí možnost není, proto platí stále stejně
\[ \textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}. \]
Pro počáteční stav \({\textbf{s}}\) a požadovaný závěrečný stav \({\textbf{t}}\) platí
\[ \textbf{s} = \begin{bmatrix}0\\1\\2\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\end{bmatrix}. \]
Podle již uvedeného zápisu
\[ \textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t}, \] můžeme sestavit soustavu tří lineárních rovnic \[ \begin{aligned} 0 + 1x_1 + 1x_2 + 0x_3 &= 0\\ 1 + 1x_1 + 1x_2 + 1x_3 &= 0\\ 2 + 0x_1 + 1x_2 + 1x_3 &= 0 \end{aligned} \] a vyřešíme ji. \[ \begin{alignedat}{3} x_1 &+ x_2& && &= 0 \\ x_1 &+ x_2& &+ x_3&&= -1\\ && x_2 &+ x_3&&= -2 \end{alignedat} \] Z prvního a třetího řádku vyjádříme \(x_1\) a \(x_3\) v závislosti na \(x_2\) \[ \begin{aligned} x_1 &= -x_2\\ x_3 &= -2-x_2 \end{aligned} \] a dosadíme do druhé rovnice \[ \begin{aligned} -x_2 + x_2 -2-x_2 &= -1 \\ -x_2 &= 1 \\ x_2 &= -1. \end{aligned} \] Ve trojkové soustavě platí \(3k=0\), \(k\in\mathbb{Z}\), \(3l+1=1\), \(l\in\mathbb{Z}\) a \(3m+2=2\), \(m\in\mathbb{Z}\), tedy \(-1=2\) nebo také \(-2=1\), a proto \(x_2 = 2\), \(x_1 = -2 = 1\) a \(x_3 = -1 = 2\).
Výsledkem je, že když jednou zmáčkneme tlačítko A, dvakrát tlačítko B a dvakrát tlačítko C, z původního stavu na obrázku všechny žárovky zhasneme.