Wiele gier komputerowych i mobilnych opiera się na łamigłówkach, w których aby osiągnąć cel, należy wykonać określoną kombinację ruchów. Na przykład, nacisnąć niektóre z oferowanych przełączników, aby kontrolowana przez nie maszyna zadziałała. Co więcej, takie przełączniki mają skończoną liczbę stanów, w których mogą się znajdować: są albo włączone, albo wyłączone. Zademonstrujmy to na przykładzie żarówki. Jest ona albo włączona, albo wyłączona, a jej przełącznik wykonuje tylko dwie akcje. Kiedy żarówka jest wyłączona, pierwsze użycie przełącznika włącza ją, a drugie wyłącza. W informatyce istnieje wiele takich systemów, które mają ograniczoną liczbę stanów. Te gry, w których konieczne jest ustalenie optymalnej kombinacji ruchów, która da nam prawidłowy wynik, nazywane są skończonymi grami liniowymi.
Wyobraźmy sobie sieć trzech żarówek, z których każda jest wyłączona, a pod każdą z nich znajduje się przełącznik. Każdy z przełączników zmienia stan (włączony lub wyłączony) żarówek znajdujących się nad nim i jednocześnie żarówek bezpośrednio z nim sąsiadujących. Jeśli nazwiemy żarówki i odpowiadające im przełączniki A, B, C, to naciśnięcie przełącznika A zapali żarówkę A, ale ponieważ znajduje się on na krawędzi, zapali się tylko żarówka B. To samo dotyczy żarówki C, która również ma sąsiada tylko z jednej strony, więc naciśnięcie przełącznika C spowoduje zapalenie żarówek C i B. Tylko żarówka B sąsiaduje zarówno z A, jak i C, więc przełącznik B zmienia stan wszystkich trzech żarówek.
Na poniższych trzech zdjęciach możemy zaobserwować, jak żarówki stopniowo włączają się i wyłączają po naciśnięciu kolejno przycisków A i B. Należy zauważyć, że kolejność naciskania przycisków nie ma znaczenia. Możemy sobie wyobrazić, że jeśli najpierw naciśniemy przycisk B, wszystkie żarówki zaświecą się, a kolejne naciśnięcie przycisku A wyłączy żarówki A i B, tak że tylko światło żarówki C pozostanie włączone.
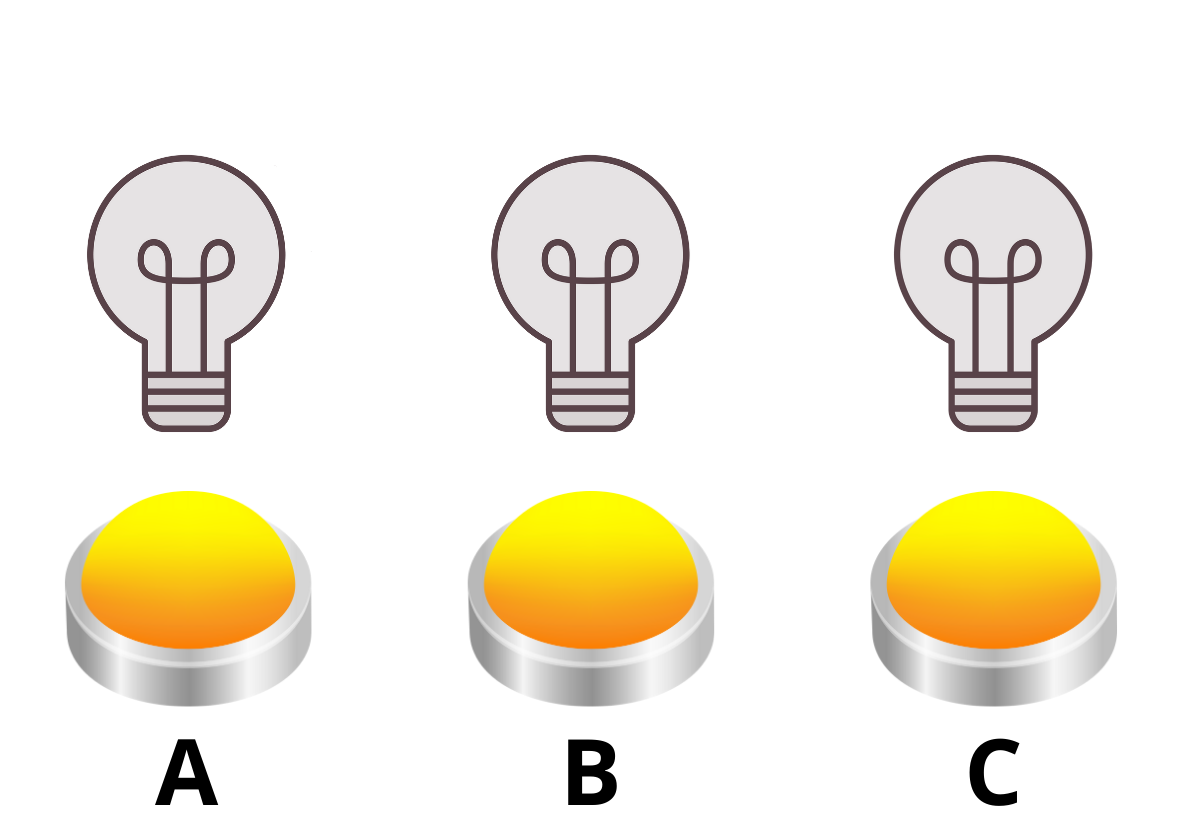
W poniższych ćwiczeniach kluczowe znaczenie ma pojęcie liczby skończonej. W przypadku żarówek, które są zawsze albo włączone, albo wyłączone, możemy zidentyfikować kilka sytuacji, które albo mają miejsce (“tak”), albo nie mają miejsca (“nie”), a ponieważ jesteśmy w matematyce, możemy użyć zamiast słów binarnego systemu oznaczania: tak = 1, nie = 0, tj.
Ponadto w układzie binarnym \(1+1=0\) lub również \(2k=0\), \(k\in\mathbb{Z}\), a jednocześnie \(1=-1\). W przypadku żarówek przekłada się to następująco. Jeśli naciśniemy ten sam przycisk dwa razy, odpowiednia żarówka włączy się i wyłączy (lub odwrotnie). Wraca do swojego pierwotnego stanu i jest taka sama, jakbyśmy w ogóle nie nacisnęli przycisku.
Wpływ każdego przycisku na wszystkie żarówki można zapisać jako wektor. Wektory \(\textbf{a}\), \(\textbf{b}\), \(\textbf{c}\) będą opisywać działanie odpowiednio przycisków A, B, C. Każda współrzędna wektora opisuje odpowiednią żarówkę w odpowiedniej kolejności: pierwsza A, druga B, trzecia C. Oznaczenie 1 oznacza, że przycisk zmienia stan tej żarówki, a 0 oznacza, że nie ma na nią wpływu. Zgodnie z powyższymi właściwościami przycisku, obowiązują następujące zasady
\[ \textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}. \]
Wektory mogą być również używane do opisywania aktualnego stanu żarówek. Żarówka jest włączona: 1, Żarówka jest wyłączona: 0. Stan początkowy, gdy żadna żarówka nie jest włączona, byłby opisany przez wektor \[ \textbf{s}=\begin{bmatrix} 0\\0\\0\end{bmatrix}. \] Naciskając kolejno przyciski A i B, dotarliśmy do trzeciego zdjęcia zapisanego przy użyciu dodawania wektorowego w systemie binarnym
\[ \textbf{s}+\textbf{a}+\textbf{b}= \begin{bmatrix}0\\0\\0\end{bmatrix}+ \begin{bmatrix}1\\1\\0\end{bmatrix}+ \begin{bmatrix}1\\1\\1\end{bmatrix}= \begin{bmatrix} 0+1+1 \\ 0+1+1 \\ 0+0+1 \end{bmatrix}= \begin{bmatrix}0\\0\\1\end{bmatrix}. \]
Zadanie 1. Określ kombinację przycisków, które należy nacisnąć, aby świeciły się tylko żarówki A i C, gdy wszystkie trzy żarówki są początkowo wyłączone.
Rozwiązanie. Pożądany stan wynikowy można opisać za pomocą wektora \[ \textbf{t}=\begin{bmatrix}1\\0\\1\end{bmatrix}. \] Rozwiązujemy zadanie jako układ równań liniowych \[\textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t}, \] gdzie współczynniki \({\textbf{a}}\), \({\textbf{b}}\), \({\textbf{c}}\) opisują, które żarówki są kontrolowane przez dany przycisk, jak wspomniano powyżej, a zmienne \(x_1, x_2, x_3\) przyjmują wartości 1 lub 0, w zależności od tego, czy użyjemy odpowiedniego przycisku, czy nie.
Za pierwszym razem przedstawimy system zawierający zerowe współczynniki, aby wyjaśnić, w jaki sposób wektory są przepisywane do systemu \({\textbf{a}}\), \({\textbf{b}}\), \({\textbf{c}}\).
\[ \begin{aligned} 0 + 1x_1 + 1x_2 + 0x_3 &= 1\\ 0 + 1x_1 + 1x_2 + 1x_3 &= 0\\ 0 + 0x_1 + 1x_2 + 1x_3 &= 1 \end{aligned} \]
Układ rozwiązujemy na przykład metodą podstawiania:
\[ \begin{alignedat}{3} x_1 &+ x_2& && &= 1 \Rightarrow x_1 = 1-x_2\\ x_1 &+ x_2& &+ x_3&&= 0\\ && x_2 &+ x_3&&= 1 \Rightarrow x_3 = 1-x_2 \end{alignedat} \]
Podstawiamy w drugim równaniu:
\[ \begin{aligned} (1-x_2) + x_2 + (1-x_2) &= 0\\ 2 - x_2 &= 0\\ x_2 &= 2, \end{aligned} \]
ale ponieważ pracujemy w systemie binarnym, gdzie \(2=0\), \(x_2 = 0\) jest prawdziwe. Po podstawieniu otrzymujemy \(x_1=1, x_3=1\), co oznacza, że musimy nacisnąć przyciski A i C, aby żarówki A i C zaświeciły się, a żarówka B zgasła.
Uwaga. Problemy z trzema żarówkami można rozwiązać bardzo łatwo, ponieważ każdy przycisk jest naciskany co najwyżej raz. Naciśnięcie więcej niż raz nie ma sensu, ponieważ dwa naciśnięcia tego samego przycisku dają taki sam wynik jak brak naciśnięcia. W poniższym zadaniu zwiększymy zatem liczbę żarówek, ale spowoduje to powstanie zestawu więcej niż trzech równań liniowych z więcej niż trzema niewiadomymi, które prawdopodobnie nie są już liczone na regularnych lekcjach matematyki. W związku z tym problemy te można wykorzystać na specjalnym seminarium, na którym studenci zapoznają się z rachunkiem macierzowym i mogą go przećwiczyć na konkretnym problemie słownym.
Zadanie 2.Rozbudujemy sieć żarówek do pięciu. Przyciski nadal mają tę samą właściwość, kontrolują żarówkę nad nimi i ich bezpośrednimi sąsiadami. Na początku nie wszystkie żarówki są wyłączone, ale żarówki A i D są już włączone.
Dowiedz się, jaką kombinację przycisków należy nacisnąć, aby uzyskać wynik - wszystkie żarówki wyłączone, - świeci tylko żarówka E.
Rozwiązanie. Oprócz liczby równań liniowych i zmiennych w systemie, rozwiązanie będzie się również różnić zmodyfikowanym stanem początkowym, gdzie wszystkie żarówki nie są w stanie 0 = wyłączone. Stan początkowy można zapisać jako wektor
\[ \textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix} \] a zachowanie przycisków od A do E jest opisane przez wektory \[ \textbf{a}=\begin{bmatrix}1\\1\\0\\0\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\\0\\0\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\\1\\0\end{bmatrix},\quad \textbf{d}=\begin{bmatrix}0\\0\\1\\1\\1\end{bmatrix},\quad \textbf{e}=\begin{bmatrix}0\\0\\0\\1\\1\end{bmatrix}. \]
Jeśli chcemy, aby wszystkie żarówki były wyłączone, rozwiązujemy następujący układ równań
\[ \textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} + x_4\textbf{d} + x_5\textbf{e}= \textbf{t}, \] gdzie \[ \textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\\0\\0\end{bmatrix}. \]
Przenosimy wektor \({\textbf{s}}\) na prawą stronę
\[ x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} + x_4\textbf{d} + x_5\textbf{e}= \textbf{t} - \textbf{s}, \] i zapisujemy układ pięciu równań liniowych z pięcioma niewiadomymi \[ \begin{alignedat}{8} x_1 &+& &x_2& && && && && && &= 0-1 \\ x_1 &+& &x_2& &+& &x_3& && && && &= 0 \\ && &x_2& &+& &x_3& &+& &x_4& && &=0 \\ && && && &x_3& &+& &x_4& &+& x_5 &=0-1 \\ && && && && && &x_4& &+& x_5 &=0 \end{alignedat} \] Podczas rozwiązywania należy pamiętać, że w systemie binarnym \(-1=1\) i \(2=0\). Jedno z równań zostanie wyzerowane, gdy wprowadzimy poprawki, co normalnie oznaczałoby nieskończenie wiele rozwiązań, ale w rachunku skończonym tak nie jest. Układ ma dwa rozwiązania, które są wektorami rzędu pięciu \((0,1,1,0,0)\) a \((1,0,1,1,1)\).
Jeśli tylko żarówka E ma pozostać włączona, obowiązują następujące zasady \[ \textbf{t} = \begin{bmatrix}0\\0\\0\\0\\1\end{bmatrix}. \] Po kilku krokach przy użyciu metody dodawania lub metody eliminacji Gaussa (podczas pracy z macierzami) okaże się, że jedno z równań układu nie ma rozwiązania, a zatem cały układ nie ma rozwiązania dla tego zadania. Dlatego nie możemy zmienić żarówek z ich pierwotnego stanu, w którym tylko A i D są włączone, do stanu, w którym tylko żarówka E jest włączona.
Zadanie 3. Nowe niebieskie żarówki różnią się od poprzednich tym, że mogą świecić w dwóch różnych odcieniach niebieskiego. Gdy żarówka jest wyłączona, pierwsze naciśnięcie przycisku, który go kontroluje, zaświeci się na jasnoniebiesko, drugie naciśnięcie zmieni kolor na ciemnoniebieski, a trzecie naciśnięcie ponownie go wyłączy. Przyciski nadal mają tę samą właściwość, to znaczy, że kontrolują żarówkę nad sobą i swoimi bezpośrednimi sąsiadami. Ile razy należy nacisnąć który z przycisków A, B i C, wyłączyć wszystkie żarówki ze stanu pokazanego na zdjęciu?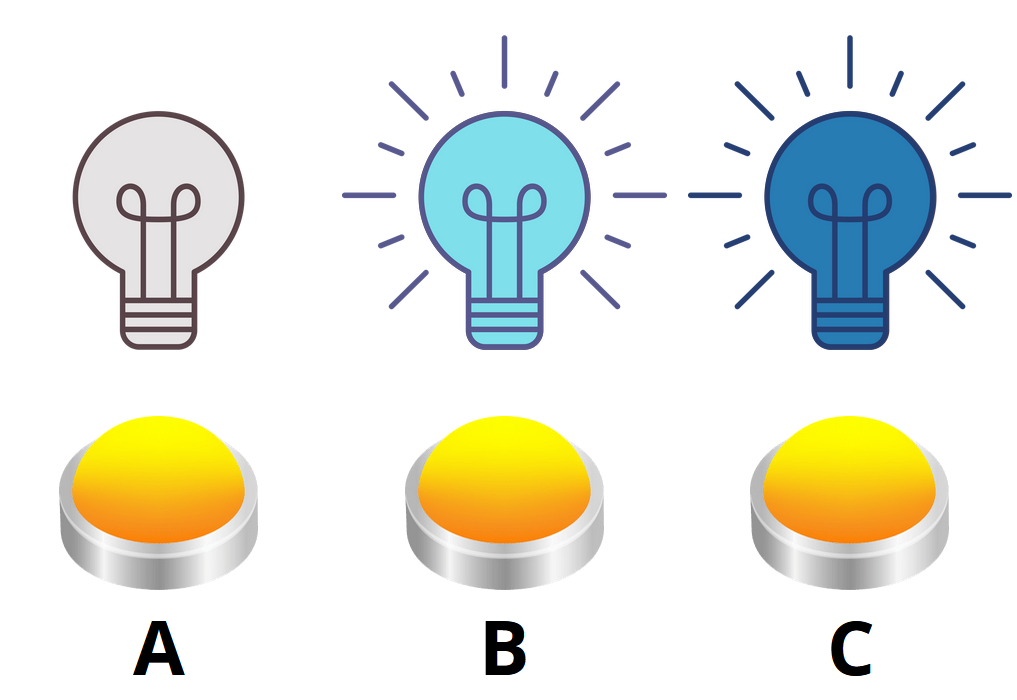 
Rozwiązanie. Ponieważ żarówki mają teraz trzy stany, w których mogą się znajdować, przechodzimy do liczenia w systemie trójskładnikowym. Oznaczmy żarówkę “nie świeci” = 0, “świeci na jasnoniebiesko” = 1 i “świeci na ciemnoniebiesko” = 2.
Jednak przyciski A, B, C mogą tylko sterować daną żarówką lub nie sterować, nie ma trzeciej opcji, więc to samo nadal obowiązuje
\[ \textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}. \]
Dla stanu początkowego \({\textbf{s}}\) i pożądanego stanu końcowego \({\textbf{t}}\) obowiązuje następująca zasada
\[ \textbf{s} = \begin{bmatrix}0\\1\\2\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\end{bmatrix}. \]
Zgodnie z poprzednim mamy
\[ \textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t}, \] i możemy zapisać układ trzech równań liniowych \[ \begin{aligned} 0 + 1x_1 + 1x_2 + 0x_3 &= 0\\ 1 + 1x_1 + 1x_2 + 1x_3 &= 0\\ 2 + 0x_1 + 1x_2 + 1x_3 &= 0 \end{aligned} \] i rozwiążemy go. \[ \begin{aligned} x_1 &+ x_2& && &= 0 \\ x_1 &+ x_2& &+ x_3&&= -1\\ && x_2 &+ x_3&&= -2 \end{aligned} \] W pierwszym i trzecim wierszu wyrażamy \(x_1\) i \(x_3\) w zależności od \(x_2\) \[ \begin{aligned} x_1 &= -x_2\\ x_3 &= -2-x_2 \end{aligned} \] i podstawiamy do drugiego równania \[ \begin{aligned} -x_2 + x_2 -2-x_2 &= -1 \\ -x_2 &= 1 \\ x_2 &= -1. \end{aligned} \] W układzie trójskładnikowym \(3k=0\), \(k\in\mathbb{Z}\), \(3l+1=1\), \(l\in\mathbb{Z}\) i \(3m+2=2\), \(m\in\mathbb{Z}\), zatem \(-1=2\) lub również \(-2=1\), a zatem \(x_2 = 2\), \(x_1 = -2 = 1\) i \(x_3 = -1 = 2\).
W rezultacie po naciśnięciu przycisku A, przycisku B dwa razy i przycisku C dwa razy, od pierwotnego stanu na zdjęciu, wszystkie żarówki gasną.