Mnohé počítačové a mobilné hry sú založené na hádankách, pri ktorých je na dosiahnutie cieľa potrebné vykonať určitú kombináciu ťahov. Napríklad stlačiť niektoré z ponúkaných spínačov tak, aby stroj ovládaný týmito spínačmi fungoval. Navyše, takéto spínače majú konečný počet stavov, v ktorých môžu byť: buď sú zapnuté, alebo vypnuté. Ukážme si to na príklade žiarovky. Tá buď svieti alebo nesvieti a jej spínač vykonáva iba dve akcie. Keď žiarovka nesvieti, prvé použitie spínača ju zapne a druhé použitie spínača ju vypne. V informatike existuje mnoho takýchto systémov, ktoré majú obmedzený počet stavov. Tieto hry, v ktorých je potrebné nastaviť optimálnu kombináciu ťahov, ktorá nám dá správny výsledok, sa nazývajú konečné lineárne hry.
Predstavme si sieť troch žiaroviek, ktoré sú na začiatku všetky vypnuté a pod každou z nich je spínač. Každý z týchto spínačov zmení stav (zapnuté alebo vypnuté) žiarovky nad ním a zároveň žiaroviek priamo susediacich s ňou. Ak označíme žiarovky a ich príslušné spínače A, B, C, potom stlačenie spínača A rozsvieti žiarovku A, ale pretože je na kraji, rozsvieti sa s ňou aj žiarovka B. To isté platí pre žiarovku C, tá má tiež suseda iba na jednej strane, takže stlačením spínača C sa rozsvietia žiarovky C a B. Iba žiarovka B susedí s oboma A aj C, takže spínač B zmení stav všetkých troch žiaroviek.
Na nasledujúcich troch obrázkoch môžeme pozorovať, ako sa žiarovky postupne rozsvietia a zhasnú pri stláčaní tlačidiel A a B. Je dôležité si všimnúť, že na poradí, v akom sú tlačidlá stláčané nezáleží. Môžeme si predstaviť, že ak by sme najprv stlačili B, všetky žiarovky sa rozsvietia, a následné stlačenie A vypne žiarovky A a B, takže svieti iba žiarovka C.
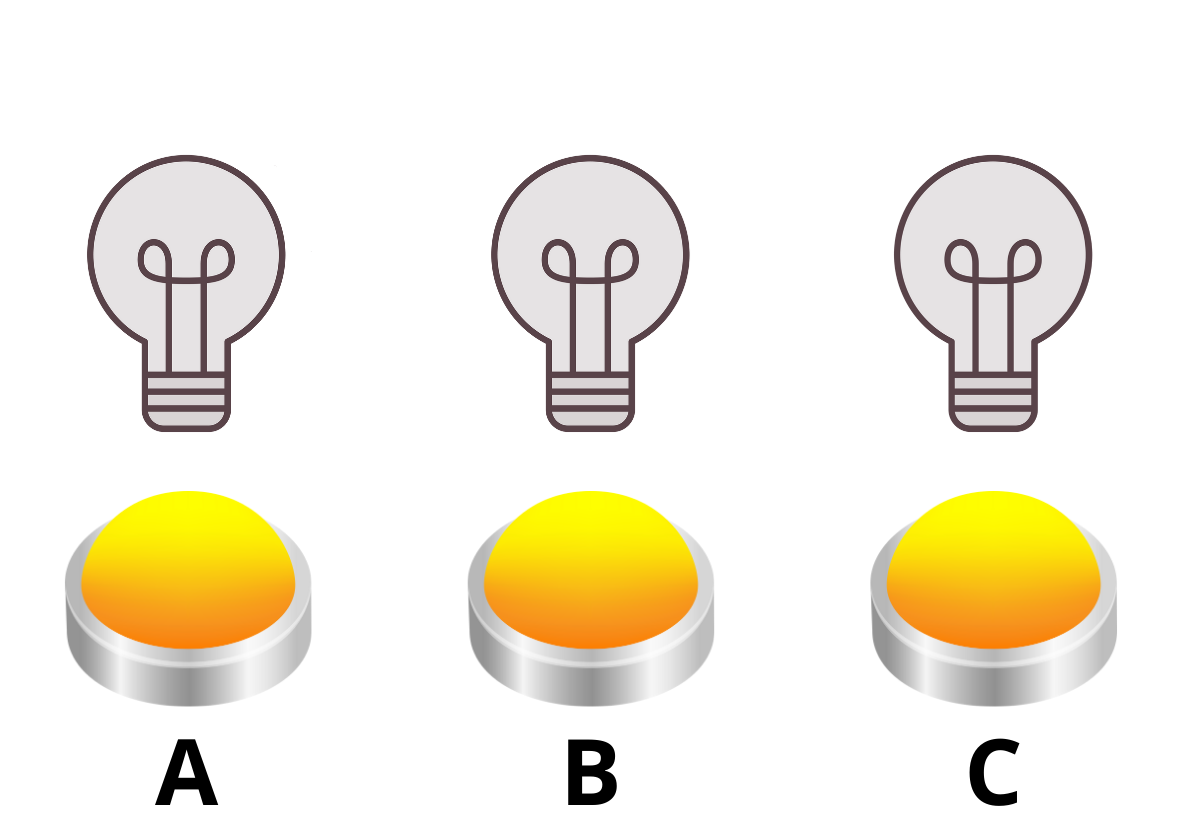
Pre nasledujúce úlohy je kľúčový koncept konečného počtu. V prípade žiaroviek, ktoré sú vždy buď zapnuté alebo vypnuté, môžeme identifikovať niekoľko situácií, ktoré buď nastávajú („áno“), alebo nenastávajú („nie“). A keďže sa nachádzame v oblasti matematiky, môžeme namiesto slov použiť binárnu sústavu označenia: áno = 1, nie = 0, t. j.
Navyše, v binárnej sústave platí \(1+1=0\) alebo tiež \(2k=0\), \(k\in\mathbb{Z}\) a zároveň \(1=-1\). V prípade žiaroviek sa to dá preložiť nasledovne. Ak stlačíme to isté tlačidlo dvakrát, príslušná žiarovka sa zapne a vypne (alebo naopak). Vráti sa do svojho pôvodného stavu a je to to isté, ako keby sme tlačidlo vôbec nestlačili.
Vplyv každého tlačidla na všetky žiarovky môžeme zapísať ako vektor. Vektory \(\textbf{a}\), \(\textbf{b}\), \(\textbf{c}\) budú popisovať činnosť tlačidiel A, B, C postupne. Každá súradnica vektora popisuje príslušnú žiarovku v príslušnom poradí: prvá A, druhá B, tretia C. Označenie 1 znamená, že tlačidlo zmení stav tejto žiarovky a 0 znamená, že na ňu nemá žiadny vplyv. Podľa uvedených vlastností tlačidiel platí \[ \textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}. \]
Vektory môžeme použiť aj na popis aktuálneho stavu žiaroviek. Žiarovka je zapnutá: 1, žiarovka je vypnutá: 0. Počiatočný stav, keď nie je zapnutá žiadna žiarovka, by bol opísaný vektorom \[ \textbf{s}=\begin{bmatrix} 0\\0\\0\end{bmatrix}. \] Postupným stlačením tlačidiel A a B sme sa dostali k tretiemu obrázku. Zapísané pomocou sčítania vektorov v binárnej sústave \[ \textbf{s}+\textbf{a}+\textbf{b}= \begin{bmatrix}0\\0\\0\end{bmatrix}+ \begin{bmatrix}1\\1\\0\end{bmatrix}+ \begin{bmatrix}1\\1\\1\end{bmatrix}= \begin{bmatrix} 0+1+1 \\ 0+1+1 \\ 0+0+1 \end{bmatrix}= \begin{bmatrix}0\\0\\1\end{bmatrix}. \]
Úloha 1. Určte kombináciu tlačidiel, ktoré musia byť stlačené, aby svietili iba žiarovky A a C, keď sú všetky tri žiarovky na začiatku vypnuté.
Riešenie. Požadovaný výsledný stav môže byť opísaný vektorom \[ \textbf{t}=\begin{bmatrix}1\\0\\1\end{bmatrix}. \] Problém riešime ako sústavu lineárnych rovníc \[\textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t}, \] kde koeficienty \({\textbf{a}}\), \({\textbf{b}}\), \({\textbf{c}}\) popisujú, ktoré žiarovky sú ovládané daným tlačidlom, ako je uvedené vyššie, a premenné \(x_1, x_2, x_3\) nadobúdajú hodnoty 1 alebo 0 v závislosti od toho, či príslušné tlačidlo použijeme alebo nie. Najprv sústavu uvedieme vrátane nulových koeficientov, aby bolo jasné, ako sú vektory \({\textbf{a}}\), \({\textbf{b}}\), \({\textbf{c}}\) prepísané do sústavy.
\[ \begin{aligned} 0 + 1x_1 + 1x_2 + 0x_3 &= 1\\ 0 + 1x_1 + 1x_2 + 1x_3 &= 0\\ 0 + 0x_1 + 1x_2 + 1x_3 &= 1 \end{aligned} \]
Sústavu riešime napríklad metódou substitúcie:
\[ \begin{alignedat}{3} x_1 &+ x_2& && &= 1 \Rightarrow x_1 = 1-x_2\\ x_1 &+ x_2& &+ x_3&&= 0\\ && x_2 &+ x_3&&= 1 \Rightarrow x_3 = 1-x_2 \end{alignedat} \]
Dosadíme do druhej rovnice
\[ \begin{aligned} (1-x_2) + x_2 + (1-x_2) &= 0\\ 2 - x_2 &= 0\\ x_2 &= 2, \end{aligned} \]
ale keďže pracujeme v binárnej sústave tak \(2=0\), potom platí \(x_2 = 0\). Dosadením, dostávame \(x_1=1, x_3=1\), čo znamená, že musíme stlačiť tlačidlá A a C, aby žiarovky A a C svietili a žiarovka B bola zhasnutá.
Poznámka. Úlohy pre tri žiarovky sa dajú veľmi ľahko vyriešiť spamäti, pretože každé tlačidlo sa stláča najviac raz. Viackrát stlačiť nemá zmysel, pretože dve stlačenia toho istého tlačidla znamená to isté, ako keby nebolo stlačené vôbec. V nasledujúcej úlohe preto zvýšime počet žiaroviek, čo však vedie k sústave s viac ako tromi lineárnymi rovnicami s viac ako tromi neznámymi, ktoré sa už pravdepodobne nepočítajú na bežných hodinách matematiky. Preto môžu byť tieto úlohy využité na seminároch, na ktorých sa študenti učia matice a môžu si ich tak precvičiť na konkrétnej slovnej úlohe.
Úloha 2. Rozšírime sieť žiaroviek na päť. Tlačidlá majú stále rovnakú vlastnosť, ovládajú žiarovku nad nimi a ich bezprostredných susedov. Na začiatku nie sú všetky žiarovky vypnuté, ale žiarovky A a D už svietia.
Zistite, akú kombináciu tlačidiel treba stlačiť, aby - všetky žiarovky boli zhasnuté, - svietila iba žiarovka E.
Riešenie. Okrem počtu lineárnych rovníc a premenných v sústave sa riešenie bude líšiť aj upraveným počiatočným stavom, kde všetky žiarovky nie sú v stave 0 = vypnuté. Počiatočný stav možno zapísať ako vektor \[ \textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix} \] a správanie tlačidiel A až E je opísané vektormi \[ \textbf{a}=\begin{bmatrix}1\\1\\0\\0\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\\0\\0\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\\1\\0\end{bmatrix},\quad \textbf{d}=\begin{bmatrix}0\\0\\1\\1\\1\end{bmatrix},\quad \textbf{e}=\begin{bmatrix}0\\0\\0\\1\\1\end{bmatrix}. \]
Ak chceme, aby boli všetky žiarovky zhasnuté, riešime nasledujúcu sústavu rovníc
\[ \textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} + x_4\textbf{d} + x_5\textbf{e}= \textbf{t}, \] kde \[ \textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\\0\\0\end{bmatrix}. \]
Vektor \({\textbf{s}}\) prevedieme na druhú stranu rovnice
\[ x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} + x_4\textbf{d} + x_5\textbf{e}= \textbf{t} - \textbf{s}, \] a zapíšeme sústavu piatich lineárnych rovníc s piatimi neznámymi \[ \begin{alignedat}{8} x_1 &+& &x_2& && && && && && &= 0-1 \\ x_1 &+& &x_2& &+& &x_3& && && && &= 0 \\ && &x_2& &+& &x_3& &+& &x_4& && &=0 \\ && && && &x_3& &+& &x_4& &+& x_5 &=0-1 \\ && && && && && &x_4& &+& x_5 &=0 \end{alignedat} \] Pri riešení si pamätajte, že v binárnej sústave platí \(-1=1\) a \(2=0\). Jedna z rovníc sa pri úpravách zmení na nulu, čo by normálne znamenalo nekonečne veľa riešení, ale v konečnom počte to tak nie je. Sústava má dve riešenia \((0,1,1,0,0)\) a \((1,0,1,1,1)\).
Ak má zostať svietiť iba žiarovka E, platí nasledovné \[ \textbf{t} = \begin{bmatrix}0\\0\\0\\0\\1\end{bmatrix}. \] Po niekoľkých krokoch pomocou metódy sčítania alebo Gaussovej eliminačnej metódy (pri práci s maticami) by sme zistili, že jedna z rovníc sústavy nemá riešenie, a preto celá sústava nemá pre tento problém riešenie. Preto nemôžeme zmeniť žiarovky z ich pôvodného stavu, kde svietia iba A a D, na stav, kde svieti iba žiarovka E.
Úloha 3. Nové modré žiarovky sa od tých predchádzajúcich líšia tým, že môžu svietiť v dvoch rôznych odtieňoch modrej. Keď je táto žiarovka vypnutá tak prvým stlačením tlačidla, ktoré ju ovláda, sa rozsvieti na svetlomodro, druhým stlačením sa zmení na tmavomodrú a tretím stlačením sa opäť vypne. Tlačidlá majú stále rovnakú vlastnosť, teda ovládajú žiarovku nad nimi a ich bezprostredných susedov. Koľkokrát musíte stlačiť ktoré z tlačidiel A, B a C, aby ste zhasli všetky žiarovky z polohy zobrazenej na obrázku?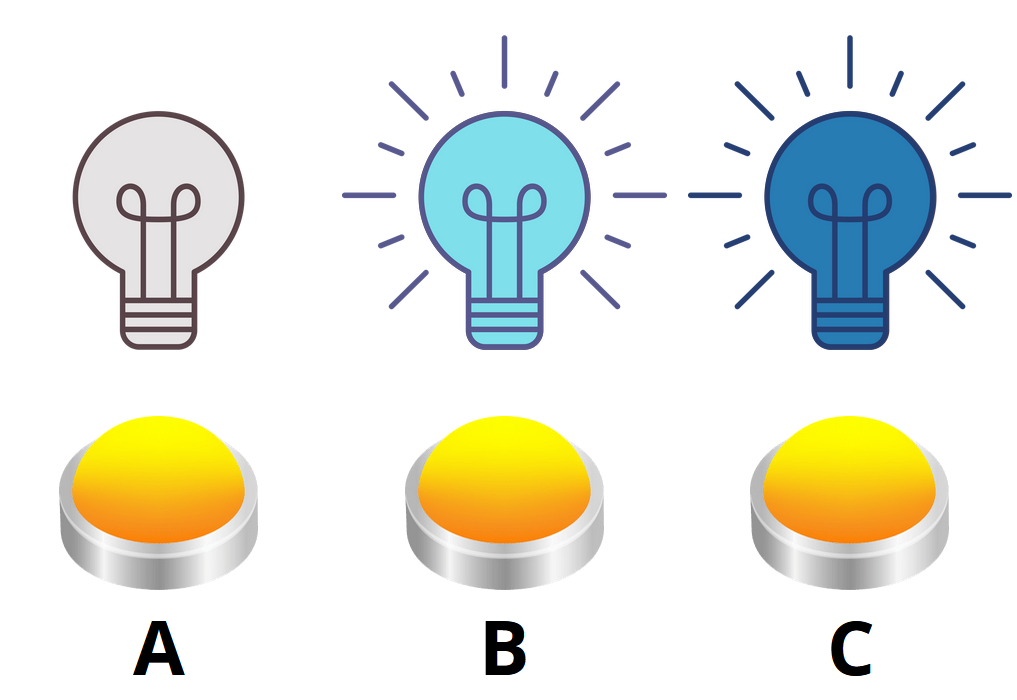 
Riešenie. Pretože žiarovky teraz môžu byť v troch stavoch, prechádzame na počítanie v trojkovej sústave. Označme si stav žiarovky „nezapnutá“ = 0, „svieti svetlomodro“ = 1 a „svieti tmavomodro“ = 2.
Tlačidlá A, B, C môžu danú žiarovku buď ovládať, alebo ju neovládať, tretia možnosť neexistuje, takže stále platí to isté
\[ \textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}. \]
Pre počiatočný stav \({\textbf{s}}\) a požadovaný konečný stav \({\textbf{t}}\) platí nasledovné
\[ \textbf{s} = \begin{bmatrix}0\\1\\2\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\end{bmatrix}. \]
Podľa predchádzajúceho zápisu máme
\[ \textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t}, \] a môžeme zapísať sústavu troch lineárnych rovníc \[ \begin{aligned} 0 + 1x_1 + 1x_2 + 0x_3 &= 0\\ 1 + 1x_1 + 1x_2 + 1x_3 &= 0\\ 2 + 0x_1 + 1x_2 + 1x_3 &= 0 \end{aligned} \] a vyriešime ju. \[ \begin{aligned} x_1 &+ x_2& && &= 0 \\ x_1 &+ x_2& &+ x_3&&= -1\\ && x_2 &+ x_3&&= -2 \end{aligned} \] Z prvého a tretieho riadku vyjadríme \(x_1\) a \(x_3\) v závislosti na \(x_2\) \[ \begin{aligned} x_1 &= -x_2\\ x_3 &= -2-x_2 \end{aligned} \] a dosadíme do druhej rovnice \[ \begin{aligned} -x_2 + x_2 -2-x_2 &= -1 \\ -x_2 &= 1 \\ x_2 &= -1. \end{aligned} \] V trojkovej sústave platí \(3k=0\), \(k\in\mathbb{Z}\), \(3l+1=1\), \(l\in\mathbb{Z}\) a \(3m+2=2\), \(m\in\mathbb{Z}\), teda \(-1=2\) alebo tiež \(-2=1\), a preto \(x_2 = 2\), \(x_1 = -2 = 1\) a \(x_3 = -1 = 2\).
Výsledok je, že ak stlačíme tlačidlo A raz, tlačidlo B dvakrát a tlačidlo C dvakrát, všetky žiarovky z pôvodného stavu na obrázku zhasnú.