Finite linear games
 40 min.,
40 min.,  2/3
2/3 Many computer and mobile games are based on puzzles in which to achieve the goal you need to perform a certain combination of moves. For example, to press some of the offered switches so the machine controlled by them, would work. Moreover, such switches have a finite number of the states in which they may be: they are either on or off. Let’s demonstrate it on example of a light bulb. It is either on or off, and its switch only performs two actions. When the bulb is off, the first use of the switch turns it on and the second use of the switch turns it off. In informatics there is many such systems that have limited number of states. Those games, in which is necessary to set up the optimal combination of moves that will give us the correct outcome is called finite linear games.
Game with three light bulbs
Imagine a network of three light bulbs that are all off at the start and under each of them there’s a switch. Each of the switches changes the state (on or off) of the bulbs above it and at the same time the bulbs directly adjacent to it. If we name the bulbs and their corresponding switches A, B, C, then pressing switch A will light bulb A, but because it is on the edge, only bulb B will light with it. The same applies to bulb C, it also has a neighbour on one side only, so pressing switch C will light up bulbs C and B. Only bulb B is adjacent to both A and C, so switch B changes the state of all three bulbs.
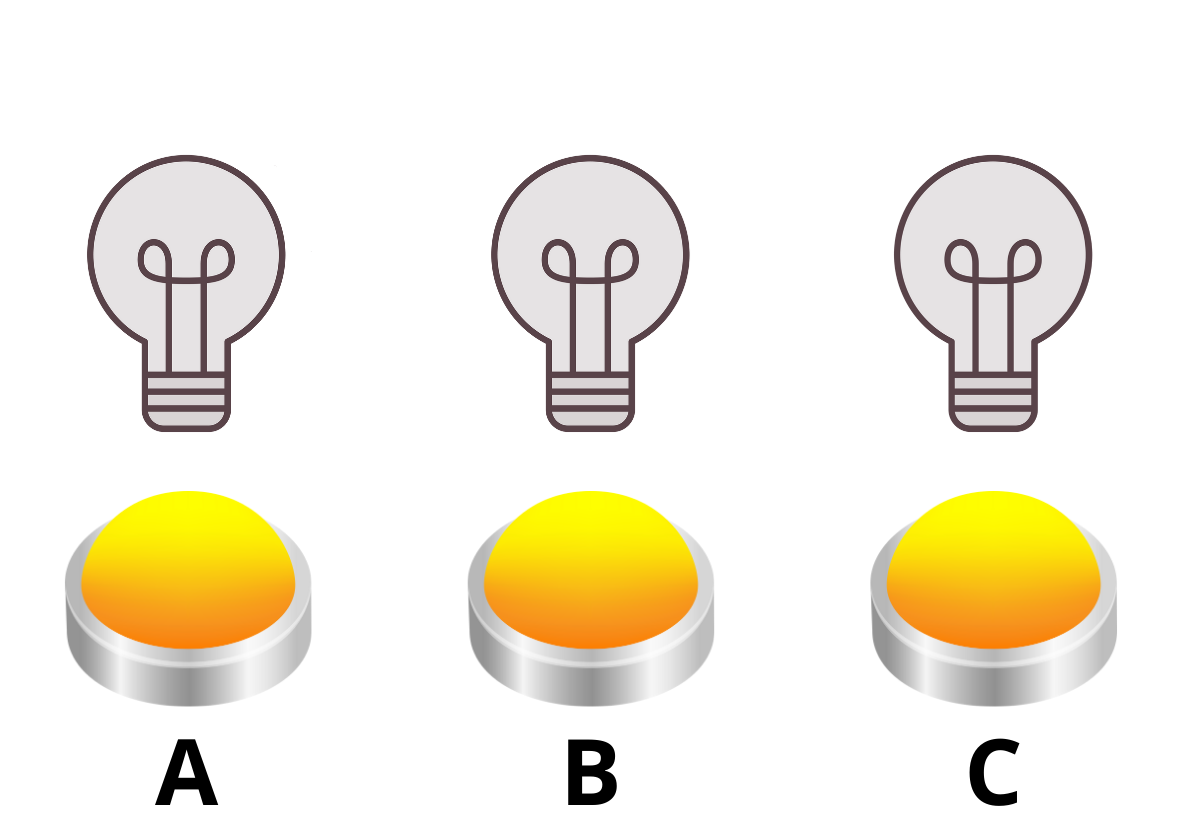
In the following three images we can observe, how the light bulbs would gradually turn on and off when pressing buttons A and B in sequence. It is important to note that the order in which the buttons are pressed does not matter. We can imagine that if we first pressed B, all the bulbs will light up, and a subsequent press A turns off bulbs A and B so only the light of bulb C stays on.


For the following exercises, the concept of a finite number is crucial. In the case of light bulbs that are always either on, or off, we can identify several situations, which are either happening (“yes”) or not happening (“no”), and since we are in math we can use instead of words binary system marking: yes = 1, no = 0, i.e.
- the bulb is on (1) or off (0),
- the button controls the bulb (1) or has no effect (0),
- the button is pressed (1) or not used (0).
In addition, in the binary system \(1+1=0\) or also \(2k=0\), \(k\in\mathbb{Z}\), and simultaneously \(1=-1\). In the case of light bulbs, this translates into following. If we press the same button twice, the corresponding bulb turns on and off (or vice versa). It goes back to its original state and it is the same, as if we hadn’t pressed the button at all.
The effect of each button on all bulbs can be written as a vector. Vectors \(\textbf{a}\), \(\textbf{b}\), \(\textbf{c}\) will describe the operation of buttons A, B, C respectively. Each coordinate of the vector describes the corresponding bulb in the corresponding order: first A, second B, third C. The designation 1 means that the button changes the state of that bulb, and 0 means it has no effect on it. According to the above button properties, the following applies
\[ \textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}. \]
The vectors can also be used to describe actual state of bulbs. The bulb is on: 1, The bulb is of: 0. The initial state, when no bulb is on, would be described by the vector \[ \textbf{s}=\begin{bmatrix} 0\\0\\0\end{bmatrix}. \] By pushing buttons A and B subsequently, we got to the third picture. Written using vector addition in the binary system
\[ \textbf{s}+\textbf{a}+\textbf{b}= \begin{bmatrix}0\\0\\0\end{bmatrix}+ \begin{bmatrix}1\\1\\0\end{bmatrix}+ \begin{bmatrix}1\\1\\1\end{bmatrix}= \begin{bmatrix} 0+1+1 \\ 0+1+1 \\ 0+0+1 \end{bmatrix}= \begin{bmatrix}0\\0\\1\end{bmatrix}. \]
Exercise 1. Determine the button combination, which must be pressed so that only bulbs A and C are on, when all three bulbs are initially off.
Solution. The desired resulting state can be described by the vector \[ \textbf{t}=\begin{bmatrix}1\\0\\1\end{bmatrix}. \] We solve the problem as a system of linear equations \[\textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t}, \] where the coefficients \({\textbf{a}}\), \({\textbf{b}}\), \({\textbf{c}}\) describe, which bulbs are controlled by a given button, as mentioned above, and the variables \(x_1, x_2, x_3\) take on the values 1 or 0, depending on whether we will use the relevant button or not.
The first time, we will present the system including zero coefficients, to make clear how the vectors are rewritten into the system \({\textbf{a}}\), \({\textbf{b}}\), \({\textbf{c}}\).
\[ \begin{aligned} 0 + 1x_1 + 1x_2 + 0x_3 &= 1\\ 0 + 1x_1 + 1x_2 + 1x_3 &= 0\\ 0 + 0x_1 + 1x_2 + 1x_3 &= 1 \end{aligned} \]
We solve the system, for example, using the substitution method:
\[ \begin{alignedat}{3} x_1 &+ x_2& && &= 1 \Rightarrow x_1 = 1-x_2\\ x_1 &+ x_2& &+ x_3&&= 0\\ && x_2 &+ x_3&&= 1 \Rightarrow x_3 = 1-x_2 \end{alignedat} \]
We substitute in the second equation:
\[ \begin{aligned} (1-x_2) + x_2 + (1-x_2) &= 0\\ 2 - x_2 &= 0\\ x_2 &= 2, \end{aligned} \]
but since we are working in a binary system where \(2=0\), \(x_2 = 0\) holds. By substituting, we get \(x_1=1, x_3=1\), which means that we have to press the A and C buttons to achieve the that bulbs A and C will be on and bulb B will be off.
Note. The problems for three bulbs can be solved very easily off the top of the head, since each button is pressed at most once. Pressing more than once doesn’t make sense because two presses of the same button come out the same as no press. In the following problem, we therefore increase the number of bulbs, but this will result in a set of more than three linear equations with more than three unknowns, which are probably no longer counted in regular mathematics classes. Therefore, the problems can be used in a special seminar, in which students are introduced to matrix calculus and can thus practise it on a specific word problem.
Exercise 2. We will expand the bulb network to five bulbs. The buttons still have the same property, they control the bulb above them and their immediate neighbours. At the beginning, not all the bulbs are off, but bulbs A and D are already on.

Find out what combination of buttons to press to end up with - all the bulbs off, - only bulb E on.
Solution. In addition to the number of linear equations and variables in the system, the solution will also differ by a modified initial state, where all the bulbs are not in the 0 = off state. The initial state can be written as the vector
\[ \textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix} \] and the behaviour of buttons A to E is described by vectors \[ \textbf{a}=\begin{bmatrix}1\\1\\0\\0\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\\0\\0\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\\1\\0\end{bmatrix},\quad \textbf{d}=\begin{bmatrix}0\\0\\1\\1\\1\end{bmatrix},\quad \textbf{e}=\begin{bmatrix}0\\0\\0\\1\\1\end{bmatrix}. \]
If we want all the bulbs to be off, we solve the following system of equations
\[ \textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} + x_4\textbf{d} + x_5\textbf{e}= \textbf{t}, \] where \[ \textbf{s} = \begin{bmatrix}1\\0\\0\\1\\0\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\\0\\0\end{bmatrix}. \]
We move the vector \({\textbf{s}}\) to the right side
\[ x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} + x_4\textbf{d} + x_5\textbf{e}= \textbf{t} - \textbf{s}, \] and we write down a system of five linear equations with five unknowns \[ \begin{alignedat}{8} x_1 &+& &x_2& && && && && && &= 0-1 \\ x_1 &+& &x_2& &+& &x_3& && && && &= 0 \\ && &x_2& &+& &x_3& &+& &x_4& && &=0 \\ && && && &x_3& &+& &x_4& &+& x_5 &=0-1 \\ && && && && && &x_4& &+& x_5 &=0 \end{alignedat} \] When solving, remember that in a binary system, \(-1=1\) and \(2=0\). One of the equations will be reset to zero when we make adjustments, which would normally mean infinitely many solutions, but in finite calculus, this is not the case. The system has two solutions, which are vectors of order five \((0,1,1,0,0)\) a \((1,0,1,1,1)\).
If only bulb E is to remain on, the following applies \[ \textbf{t} = \begin{bmatrix}0\\0\\0\\0\\1\end{bmatrix}. \] After a few steps using the addition method or the Gaussian elimination method (when working with matrices) we would find that one of the equations of the system has no solution, and therefore the whole system has no solution for this problem. That is why we cannot change the bulbs from their original state where only A and D are on, to a state where bulb E alone is on.
Exercise 3. The new blue light bulbs differ from the previous ones in that, that they can glow in two different shades of blue. When this bulb is off, the first press of the button, which controls it, it will light up in light blue, the second press turns it dark blue and the third press turns it off again. The buttons still have the same property, that is, they control the bulb above them and their immediate neighbours. How many times you have to press which of the buttons A, B and C, to turn off all the bulbs from the state shown in the picture? 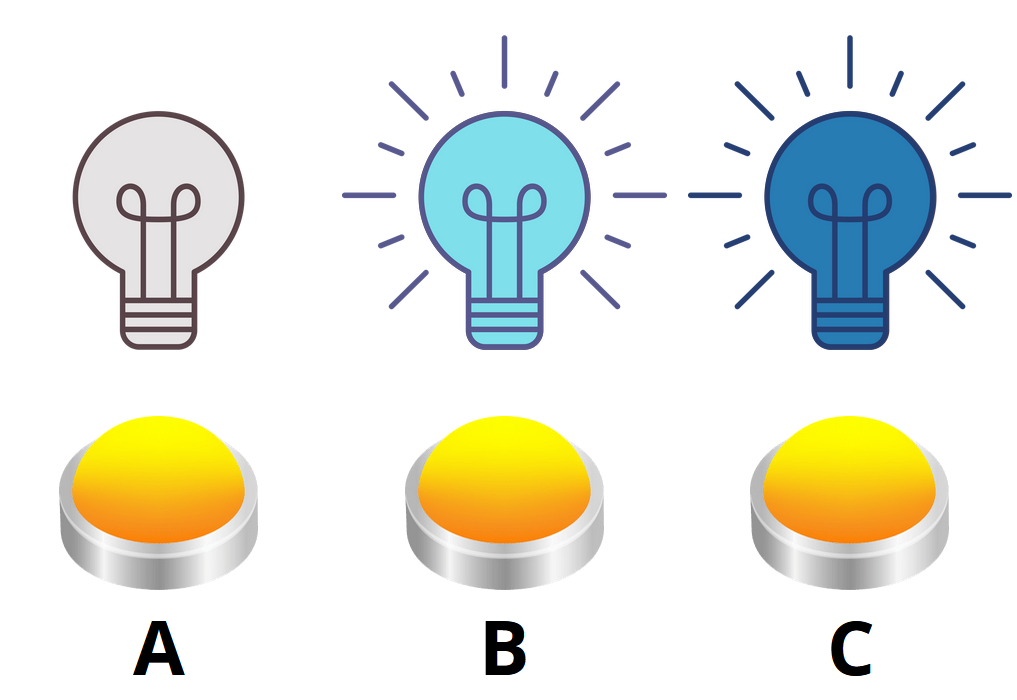
Solution. Because the bulbs now have three states, they can be in, we move on to counting in in a ternary system. Let’s denote the bulb “not lit” = 0, “glows light blue” = 1 and “glows dark blue” = 2.
However, buttons A, B, C can only control the given bulb, or not to control, there is no third option, so the same still apply
\[ \textbf{a}=\begin{bmatrix}1\\1\\0\end{bmatrix},\quad \textbf{b}=\begin{bmatrix}1\\1\\1\end{bmatrix},\quad \textbf{c}=\begin{bmatrix}0\\1\\1\end{bmatrix}. \]
For the initial state \({\textbf{s}}\) and the desired final state \({\textbf{t}}\) the following applies
\[ \textbf{s} = \begin{bmatrix}0\\1\\2\end{bmatrix}, \quad \textbf{t} = \begin{bmatrix}0\\0\\0\end{bmatrix}. \]
According to the previous we have
\[ \textbf{s} + x_1\textbf{a} + x_2\textbf{b} + x_3\textbf{c} = \textbf{t}, \] and we can write down a system of three linear equations \[ \begin{aligned} 0 + 1x_1 + 1x_2 + 0x_3 &= 0\\ 1 + 1x_1 + 1x_2 + 1x_3 &= 0\\ 2 + 0x_1 + 1x_2 + 1x_3 &= 0 \end{aligned} \] and we will solve it. \[ \begin{aligned} x_1 &+ x_2& && &= 0 \\ x_1 &+ x_2& &+ x_3&&= -1\\ && x_2 &+ x_3&&= -2 \end{aligned} \] From the first and third lines we express \(x_1\) and \(x_3\) depending on \(x_2\) \[ \begin{aligned} x_1 &= -x_2\\ x_3 &= -2-x_2 \end{aligned} \] and substitute into the second equation \[ \begin{aligned} -x_2 + x_2 -2-x_2 &= -1 \\ -x_2 &= 1 \\ x_2 &= -1. \end{aligned} \] In the ternary system holds \(3k=0\), \(k\in\mathbb{Z}\), \(3l+1=1\), \(l\in\mathbb{Z}\) and \(3m+2=2\), \(m\in\mathbb{Z}\), therefore \(-1=2\) or also \(-2=1\), and therefore \(x_2 = 2\), \(x_1 = -2 = 1\) a \(x_3 = -1 = 2\).
The result is that once we press the A button, button B twice and button C twice, from the original state in the picture, all the bulbs go off.