Golpe a una pelota de golf
 30 min.,
30 min.,  3/3
3/3 Movimiento oblicuo de proyectiles
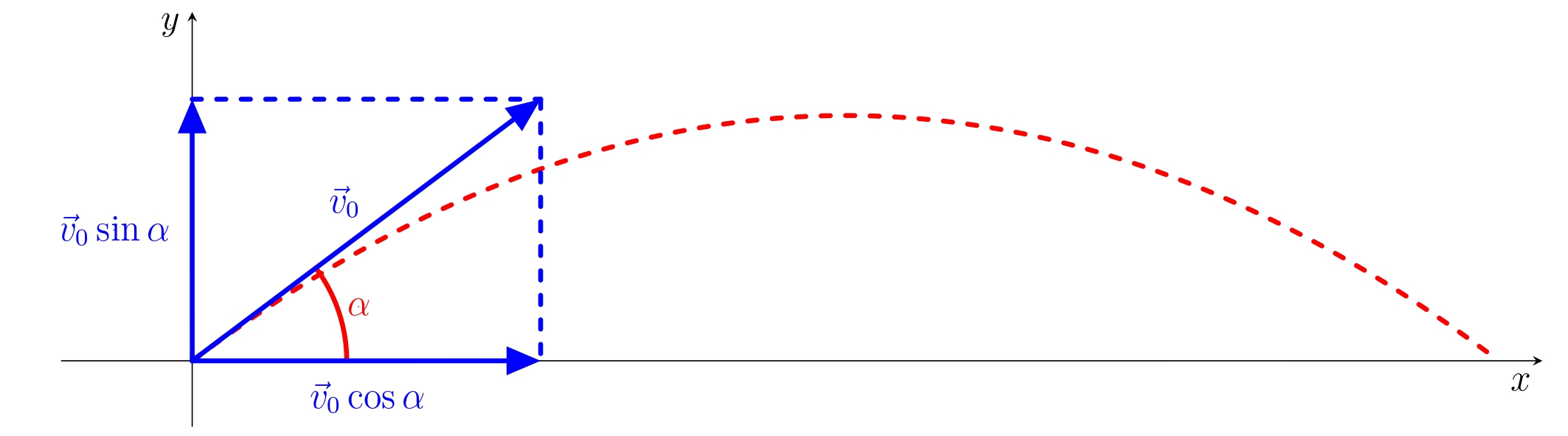
El movimiento de proyectil es la forma más general de poner en movimiento un objeto en un campo gravitatorio homogéneo. Supongamos que un cuerpo (masa puntual) es lanzado oblicuamente al espacio sin resistencia. La velocidad inicial es \(\vec{v}_0\) y el ángulo entre el vector \(\vec{v}_0\) y la dirección horizontal es \(\alpha\). Introduzcamos el sistema de coordenadas cartesianas con eje horizontal \(x\) y eje vertical \(y\) como se muestra en la imagen. Las coordenadas del vector velocidad inicial son
\[\vec{v}_0=(v_0\cos\alpha,v_0\sin\alpha).\]
El movimiento del cuerpo se rige por una aceleración debida a la gravedad \(g\) dirigida verticalmente hacia abajo. La componente horizontal de la aceleración gravitatoria es nula, por lo que el movimiento en la dirección horizontal no se ve afectado por el campo gravitatorio. La componente vertical del movimiento se ve afectada por la aceleración negativa \(-g\). Por lo tanto, se trata de un movimiento con deceleración constante (uniforme) y velocidad inicial \(v_0t\sin\alpha\).
Podemos utilizar las fórmulas de la distancia del movimiento con velocidad constante y aceleración constante para cuantificar las coordenadas de la masa puntual. Al hacerlo obtenemos \[ \begin{aligned} x(t) &= v_0 t\cos\alpha,\\ y(t) &= v_0t\sin\alpha-\frac{1}{2}gt^2. \end{aligned}\tag{1} \]
Movimiento de una bola de golf
Un golfista golpea una bola con una velocidad inicial \(v_0\). El ángulo entre la velocidad inicial y el plano horizontal es \(\alpha\). Supongamos que la fuerza de arrastre es despreciable. El movimiento de la pelota satisface por tanto las condiciones para el movimiento de un lanzado en ángulo en un entorno sin resistencia del aire.
Ejercicio 1. Demostrar que la trayectoria de la pelota de golf sigue una trayectoria parabólica.
Solución. Para encontrar la ecuación de la trayectoria en la forma \(y=f(x)\) es necesario eliminar el parámetro \(t\) del sistema (1).
Resolvemos la primera ecuación con respecto al tiempo \(t=\frac{x}{v_0\cos\alpha}\) y sustituimos en la segunda ecuación: \[y(x) = v_0\sin\alpha\,\frac{x}{v_0\cos\alpha} -\frac{1}{2}g\frac{x^2}{v_0^2\cos^2\alpha}= -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\] A partir de aquí vemos que la coordenada \(y\) de la trayectoria es una función cuadrática de la coordenada \(x\) y la trayectoria de la pelota de golf está por tanto descrita por una parábola.
Ejercicio 2. Calcular la altura del lanzamiento, es decir, la máxima altura \(y_{max}\) que alcanza la bola lanzada.
Solución. La altura del lanzamiento (movimiento del proyectil) es el máximo de la función del ejercicio anterior: \[f\colon y = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ .\]
Calculamos la derivada de la función \(f\) como
\[ y'=-\frac{g}{2v_0^2\cos^2\alpha}\cdot2x+\frac{\sin\alpha}{\cos\alpha}\ . \] Para encontrar el punto estacionario, fijamos la derivada igual a cero y obtenemos la ecuación \[ \frac{g}{v_0^2\cos^2\alpha}\cdot x=\frac{\sin\alpha}{\cos\alpha}\ . \] La solución de esta ecuación es \[ x_{max}=\frac{v_0^2\sin\alpha\cos\alpha}{g}\ . \] Dado que la trayectoria del movimiento es una función cuadrática cóncava hacia abajo, el punto estacionario localizado es el máximo y la coordenada vertical de este punto es la altura del lanzamiento.
La altura del lanzamiento se calcula evaluando la función \(f\) en la coordenada obtenida \(x_{max}\): \[y_{max}=\frac{v_0^2\sin^2\alpha}{2g}\ .\]
Ejercicio 3. Dada una velocidad inicial constante, encontrar el ángulo \(\alpha\) que garantice la máxima distancia entre el punto inicial y el punto terminal de la trayectoria.
Solución. Para encontrar el ángulo de alcance máximo necesitamos obtener el punto terminal \(x_d\) de la trayectoria en función del ángulo \(\alpha\) y encontrar el máximo de la función \(x_d(\alpha).\) Dado que \(y=0\) cuando la pelota toca el suelo, encontramos ceros de la función \[y(x) = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x.\] De aquí obtenemos: \[0 = -\frac{g}{2v_0^2\cos^2\alpha}\cdot x^2+\frac{\sin\alpha}{\cos\alpha}\cdot x\ ,\] \[0 = x\cdot\left(-\frac{g}{2v_0^2\cos^2\alpha}\cdot x+\frac{\sin\alpha}{\cos\alpha}\right)\ .\] Esta ecuación factorizada tiene dos soluciones. La primera solución \(x=0\) corresponde al lugar de lanzamiento de la pelota y la segunda solución \(x_d\) al lugar de impacto \[ x_d(\alpha) = \frac{2v_0^2\sin\alpha\cos\alpha}{g}=\frac{v_0^2}{g}\sin2\alpha\ . \] Ahora tenemos que encontrar el máximo de la función \(x_d(\alpha)\). Es suficiente para encontrar el punto estacionario, ya que se ha demostrado que la trayectoria es una parábola que se abre hacia abajo. Calculamos la derivada de la función \(x_d(\alpha)\) con respecto a \(\alpha\)
\[ x_d'(\alpha)=\frac{v_0^2}{g}\cdot\cos2\alpha\cdot 2\ . \]
Fijando la derivada igual a cero, obtenemos \(\cos2\alpha=0\), que se satisface para \(2\alpha=90^\circ\) (para que la bola se lance, obviamente \(\alpha\in\langle0^\circ,90^\circ\rangle\), por lo que la solución es inequívoca). Por tanto, el punto estacionario es \(\alpha=45^\circ\).
El alcance máximo en golf se consigue cuando se golpea la pelota con un ángulo \(\alpha=45^\circ\) y la pelota cae a una distancia de \[ x_d(45^\circ) =\frac{v_0^2}{g}\sin(2\cdot45^\circ)=\frac{v_0^2}{g}. \]
Nótese que es posible obtener la función \(x_d(\alpha) = \frac{v_0^2}{g}\sin2\alpha\) sin cálculo utilizando la simetría de la parábola. El vértice de la parábola se encuentra en el medio de los puntos cero. Por tanto, la coordenada \(x\) del punto de impacto puede cuantificarse como \(x_d(\alpha) = 2\cdot x_{max}\).
Esto nos permite evitar la resolución de la ecuación cuadrática que se obtiene sustituyendo \(y=0\) en la función \(y(x)\) y factorizando el lado derecho.
Literature
- Kubera, Miroslav; Nečas, Tomáš; Beneš, Vojtěch. Online učebnice fyziky pro gymnázia - Vrhy [online]. Available from https://e-manuel.cz/kapitoly/pouziti-pohybovych-zakonu/vyklad/vrhy/ [cit. 27.9.2023].
- Moc, Ondřej; Eisenmann, Petr. Šikmý vrh z rozhledny [online]. Available from https://mfi.upol.cz/files/26/2602/mfi_2602_129_137.pdf [cit. 27.9.2023]